数论 --- 欧拉函数、筛法求欧拉函数、欧拉定理、费马小定理详细证明

欧拉函数

什么是欧拉函数？

欧拉函数_百度百科

在数论，对正整数 n，欧拉函数是小于 n 的正整数中与 n 互质的数的数目

怎么求欧拉函数？

下面给出求欧拉函数的公式，N 分解质因数的结果为 p1^α1 × p2^α2 × . . . × pk^αk，求一个数的欧拉函数需要先对它分解质因数，那么欧拉函数 φ(N) 的结果如下

 

基于算术基本定理，对于一个整数 N 分解质因数的结果为 p1^α1 * p2^α2 * . . . * pk^αk

下面给出公式推导，运用容斥原理证明

怎么求 1 ~ n 中和 n 互质的数的个数？n 分解质因数后的结果，也就是 n 的质因子只有 p1、p2. . .pk

如果一个数是 p1 的倍数，也是 p2 的倍数，被去掉两次，但是它只能被去掉一次，所以需要把多去掉的一次加回来，加上所有 pi × pj 的倍数，也就是所有两个质数的组合( i 和 j 从 1 ~ k 中任选两个数 )

如果一个数是 p1、p2、p3 的倍数，会先被 p1 减一次，再被 p2 减一次，再被 p3 减一次，减了 3 次，然后被 p1 × p2 加一次，被 p1 × p3 加一次，被 p2 × p3 加一次，加上 3 次，实际上需要把它去掉

时间复杂度分析

瓶颈在分解质因数上，时间复杂度为 O( √ n )

题目一共有 n 个数，时间复杂度为 O( n √ ai )，O( 100 × 4 w ) = O( 400 w )

#include <iostream>
#include <algorithm>
 
using namespace std;
 
int main()
{
    int n;
    cin >> n;
    while(n --) 
    {
        int a;
        cin >> a;
        //答案
        int res = a;
        //分解质因数
        for(int i = 2;i <= a / i;i++ )
            //如果 a 能整除 i 说明 i 是 a 的质因子
            if(a % i == 0) 
            {
                //欧拉函数
                res = res / i * (i - 1); /* res * (1 - 1 / a) -> res / a * (a - 1) */ 
                while(a % i == 0) a /= i;
            }
        //a有一个大的质因子
        if(a > 1) res = res / a * (a - 1);
        cout << res << endl;
    }
    return 0;
}

筛法求欧拉函数

上一题是求某一个数的欧拉函数，这一题是求 1 ~ n 每一个数的欧拉函数，如果按照上一题的做法需要把每一个数分解质因数，时间复杂度比较高 O( n √ n )，使用线性筛求素数的方法，可以用 O( n ) 的时间复杂度计算出每一个数的欧拉函数

数论 --- 朴素筛法、埃氏筛法、线性筛法_小雪菜本菜的博客-CSDN博客

如果一个数 p 是质数，它的欧拉函数是多少？

欧拉函数的定义：在 1 ~ p 中有多少个数和 p 互质，显然 1 ~ p - 1 都是和 p 互质的，所以一个质数 p 的欧拉函数就是 p - 1

如果 i mod pj = 0，primes[ j ] * i 的欧拉函数是多少?

如果 i mod pj = 0，说明 pj 是 i 的质因子，所以在求 φ( i ) 的过程中就已经乘过 1 - 1 / pj

求欧拉函数的过程中，只要包含一个质因子 pi，就要乘上 1 - 1 / pi，与质因子的次数无关，只要出现过就要乘上 1 - 1 / pi

i 的所有质因子是 p1 ~ pk，φ( pj × i ) 分解质因数后的结果只是比 φ( i ) 多乘一项 pj 而已，由于 pj 是 i 的质因子，所以在φ( i ) 的表达式里面就已经乘过 1 - 1 / pj，pj × i 的所有质因子都是在 i 中出现过的

 

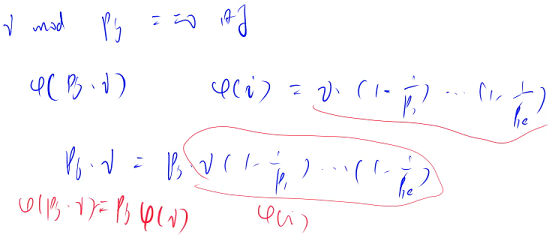
如果 i mod pj ≠ 0，说明 pj 是 i × pj 的最小质因子，而且 pj 不包含在 i 的质因子当中

#include <iostream>
#include <algorithm>
 
using namespace std;
 
const int N = 1000010;
 
//和可能会爆int 时间复杂度为n^2
typedef long long LL;
 
int n;
 
//存储每一个质数 质数的下标
int prime[N], cnt;
 
//st 表示每个数是否已经被筛掉
bool st[N];
 
//欧拉函数
int phi[N];
 
//求欧拉函数
LL get_eulers(int n)
{
    //特殊规定 φ(1) = 1,1 ~ 1 中与 1 互质的个数只有 1 
    phi[1] = 1;  
    //线性筛法 i 从 2 开始枚举
    for(int i = 2;i <= n;i++ )
    {    
        //如果当前数没有被筛过 说明当前 i 是一个质数
        if(!st[i])        
        {
            primes[cnt ++] = i;
            //如果一个数是质数 它的欧拉函数如下
            phi[i] = i - 1;
        }  
        for(int j = 0;primes[j] <= n / i;j++ )
        {
            st[primes[j] * i] = true;
            //这种情况下 primes[j] * i 的欧拉函数是多少?
            if(i % primes[j] == 0) 
            {
                phi[primes[j] * i] = phi[i] * primes[j]; /* primes[j] * phi[i] */
                break;
            }
            //if(i % primes[j] != 0) 
            //整理成类似的形式
            phi[primes[j] * i] = phi[i] * (primes[j] - 1);
        }
    }    
    //计算总和
    LL res = 0;
    for(int i = 1;i <= n;i++ ) res += phi[i];
    return res;
} 
 
int main()
{
    int n;
    cin >> n;
    //求 1 ~ n 当中每一个数的欧拉函数的和 
    cout << get_eulers(n) << endl;
 
    return 0;
}

欧拉定理

欧拉定理_百度百科

如果正整数 a 与 n 互质(最大公约数为 1)，则 a^φ( n ) 模 n 余 1

假设 1 - n 当中所有和 a 互质的数为 a1、a2 . . . aφ(n)，由于 a 和 n 互质，所以 a × a1、a × a2 . . . a × aφ(n) 每一个数也是和 n 互质的，因为 a 和 n 互质，每一个 ai 都和 n 互质，而且这 φ(n) 个数两两不同，推导出它们的数其实是相同的，只是顺序不一样

 

费马小定理_百度百科

同余定理_百度百科

证明欧拉定理

a 与 n 互质(最大公约数为 1)，3 与 10 互质，7 与 10 互质

3^4 等于 81，模 10 余 1，7^4 等于 2401，模 10 余 1

当 n 比较大的时候不好处理 φ( n )，这时我们可以运用公式

φ( n ) 等于 n 乘上从 1 到 n 之间所有质因数 p 构成的 1 - 1 / p 的乘积

这个什么意思呢？下面举一个例子

先对 1000 做质因数分解，也就是分解成质数的乘积，等于 2^3 × 5^3，所以质因数只有 2 和 5，也就是 p 只能取 2 和 5

φ(1000) = 1000 × (1 - 1 / 2) × (1 - 1 / 5) = 400

如果 n 是一个质数 p，φ( p ) 等于多少呢？

在小于质数 p 的正整数中，每一个数都和它互质，所以总个数就是 p - 1

如果正整数 a 和 p 互质，那么 a^p-1 模 p 余 1，也就是费马小定理，所以其实费马小定理就是欧拉定理的一个特例

接下来证明欧拉定理

假设选取一个数 n，在小于 n 的正整数中和 n 互质的数个数为 φ(n) 个，记作 b1、b2、. . . 、bφ( n )

再取一个和 n 互质的正整数 a，然后分别乘上 b1、b2、. . . 、bφ( n )，很明显这些数还是会与 n 互质，其中会不会有两个数的同余是一样的呢？

由于 n 和 a 是互质的，也就是 n 只能整除 bi - bj， bi 和 bj 的范围是 (1，n - 1)，也就是 bi 只能等于 bj，也就是一个数，说明这些数模 n 之后是不同的，或者说这些数模 n 之后是 b1、b2、. . . 、bφ( n ) 的重新排列

由于两边的数都是和 n 互质的，得到 a^φ( n ) 模 n 余 1，得证欧拉定理

推导欧拉函数

把 n 分解质因数，e1 - ek 是对应的次数，1000 = 2^3 × 5^3，也就是 p1 等于 2，p2 等于 5

假设 n 只含有一个质因数，也就是 n = p1^e1，φ(n) 其实就是 1 ~ n 里面和 n 互质的数的个数，反过来考虑，和 n 不互质就说明含有相同的质因数，既然 n 只有一个质因数，所以只要是 p1 的倍数都会和 n 不互质，这样的数有几个呢？总共有 n 个数，只要用总数除以 p1，就可以得到 p1 的倍数的个数有几个，这些数都与 n 不互质，包括 n 自己，所以和 n 互质的个数就是 n 减去这些数，很明显，它是符合 φ(n) 的形式的

拓展一下，如果此时 n 有两个质因数，那么从 1 ~ n 之间和 n 互质的数有多少个呢？与上面一样，其实就是要找出这些数当中是 p1 的倍数或者是 p2 的倍数但是当中有些数同时是 p1 和 p2 的倍数，这些数在统计的时候计算了两次，需要去掉一次