• 如何利用堆来模拟堆排序

    目录

    1. 堆排序是什么：

    2. 堆排序的基本思想以及实现思路：

    2.1 堆排序的基本思想：

    2.2 对于上述代码的优化：

    3. 对于升序，降序堆排序的分析：

    3.1 对于升序堆排序的分析：

    3.2 降序排序：

    4. 向下调整健堆以及两种建堆方法的优劣：

    4.1 向下调整建堆：

    4.1.1 向下建堆思路分析：

    ​编辑 4.1.2 向下调整建堆代码分析：

    4.2 两种建堆方法的优劣性分析：

    4.2.1 向下调整时间复杂度分析：

    4.2.2 向上调整时间复杂度分析：

    5. 堆排序的时间复杂度：

    1. 堆排序是什么：

    在上篇文章中，介绍了二叉树中的一种特殊结构——堆及堆的代码实现，堆可以分为大堆（父结点中存储的数值大于子结点），小堆（父结点中存储的数值小于子结点）。堆排序，正是利用堆这种数据结构的性质，以及对于堆的相关操作而设计的一种排序方法。在之前的文章中，引入了qsort(快速排序）这种排序方法，以及冒泡排序。但是这两种排序方法，相比于堆排序，时间复杂度较大，在数据量较多的情况下执行效率低，因此，本文通过上次对于二叉树中堆的相关内容，来引入堆排序的模拟实现以及原理。

    2. 堆排序的基本思想以及实现思路：

    2.1 堆排序的基本思想：

    对于堆排序的基本思想，首先要提及上篇文章中针对堆的一个重要操作：删除堆的结点HeapPop。在上篇文章中提到，删除堆的结点，一般是指删除堆的根结点。但是，如果直接针对于堆的存储结构，进行后面元素对于前方元素进行覆盖的做法并不妥当，因为会造成堆的结构错误，例如下面的小堆：

    如果让后面的元素直接向前覆盖后，堆的逻辑结构会变成下图所示：

    堆的逻辑结构不在符合小堆的定义 。因此，上篇文章给出了正确的调整方法，即：先让根结点于最后一个结点交换，交换之后删除最后一个结点，效果如下：


    再使用调整函数Adjustdown对删除结点后的堆进行调整，调整后的堆效果如下：

    对于删除函数HeapPop函数，不光可以对堆的结点进行删除，同时，每次经过删除、调整之后，堆的根结点存储的数值都是此时堆数值最小的结点。因此，堆排序的原理，就是利用HeapPop函数的原理，每次都可以找到堆中存储数值最小的结点。（或最大的结点）。

    利用上篇文章中所构建的堆，可以模拟实现堆排序，代码如下：

    1.  
    2. #include"TreeNode.h"
    3.  
    4.  
    5. void Test1()
    6. {
    7. 	int a[] = { 65,100,70,32,50,60 };
    8. 	HP hp;
    9. 	HeapInit(&hp);
    10. 	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
    11. 	{
    12. 		HeapPush(&hp, a[i]);
    13. 	}
    14. 	printf("排序前： ");
    15. 	HeapPrint(&hp);
    16. 	printf("\n");
    17.  
    18. 	printf("排序后： ");
    19. 	while (!HeapEmpty(&hp))
    20. 	{
    21. 		printf("%d ", HeapTop(&hp));
    22. 		HeapPop(&hp);
    23. 	}
    24.  
    25.  
    26. 	HeapDestory(&hp);
    27.  
    28. }
    29. int main()
    30. {
    31. 	Test1();
    32. 	return 0;
    33. }

    运行结果如下：

    上述代码虽然可以达到堆排序的效果，但是，有两个缺陷：

    1. 在排序前需要提前创建好堆。

    2. 建堆的过程需要创建数组之外的额外的空间。

    2.2 对于上述代码的优化：

    为了解决上述两个问题，采用Adjustup的思路，将数组的首元素看作根结点，对于后续结点，直接利用Adjustup函数，来构建堆，代码如下：

    1. void HPqort(int* a, int n)
    2. {
    3. 	for (int i = 0; i < n; i++)
    4. 	{
    5. 		Adjustup(a, i);
    6. 	}
    7. }
    8.  
    9. int main()
    10. {
    11. 	Test1();
    12. 	int a[] = { 70,65,100,32,50,60 };
    13. 	HPqort(a, sizeof(a) / sizeof(int));
    14. 	return 0;
    15. }

    为了方便理解，下面对于上述建堆过程给出图形演示：

    首先插入第一个结点：

    在插入第二个结点时，Adjustup函数会对新结点的数值和堆中已有的结点进行比较， 判定新插入结点存储的数值大小，小于堆中原有结点，因此，二者调换位置，效果如下：

    在插入第三个结点时，依旧重复上述过程，效果如下：

    在插入第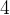4个结点时，会作为存储70的结点的子结点进行插入，经过Adjustup判定调整后，结构如下：

    插入第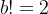5结点时，重复上述操作，效果如下：

    最后插入结点时，效果如下：

    在解决了上述代码需要提前创建堆的问题后，下一步就是对已有的堆进行排序。

    堆排序可以分为两种，即升序堆排序，降序堆排序。

    3. 对于升序，降序堆排序的分析：

    3.1 对于升序堆排序的分析：

    对于升序，就是树的存储结构中的数值是按照从小到大排列的。符合小堆的特点，上面也说到，堆排序的实现思想，就是利用堆的HeapPop,逐一选出此时树中最小的结点。但是，如果利用小堆来实现升序排序，在某些情况下，会引起堆结构的错误。例如，给出下面的小堆：

    按照给出的思路，删除根结点，并且调整树中最小的结点到根结点，即：

    此时，堆不再满足小堆的特点，可见，建立小堆来实现升序排序，有可能会破坏堆的结构。并且，Adjustdown向下调整和Adjustup向上调整这两个操作，必须是建立在结点的子树是大堆或者小堆。因此，对于上面的情况而言，解决的办法只有从新进行一次建堆。但是这种操作过于繁琐。

    因此，对于升序排序，选择建立大堆来实现，例如给出下面的大堆：

     大体思路如下：因为堆是大堆，所以，此时堆的根结点存储的数值一定是最大的，直接让根结点与尾结点交换，即：

    在交换完成后，从存储结构中可以看到，堆中最大的一个结点，已经来到了尾部。对于逻辑结构来说，如果直接让堆访问数据的数量减少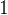1，即不再记录100，此时堆的逻辑结构和存储结构如下：

    （注：存储结构中的红线后面的数据表示不再允许访问，但并不是删除，对应到代码操作上就是size--）

    操作完成后，对于堆逻辑结构，其根结点的两个子树，依旧是大堆，所以，此时的堆可以利用上面提到的调整函数进行调整，进而选出此时树中最大的结点，再将这个结点与尾结点交换，重复上述操作。即可完成升序排序。

    对于升序堆排序的代码，一共可以分为三个部分，建立大堆的函数Adjustup，向下调整函数Adjustdown，交换函数Swap。

    对于建立大堆的函数Adjustup,需要堆结点的大小进行判定，如果后续结点中存储数值的大小大于前一个结点，则两个结点交换，代码如下：
     

    1. void Adjustup(HPDataType* a, int child)
    2. {
    3. 	assert(a);
    4.  
    5. 	int parent = (child - 1) / 2;
    6. 	while (child > 0)
    7. 	{
    8. 		if (a[child] > a[parent])
    9. 		{
    10. 			Swap(&a[child], &a[parent]);
    11. 			child = parent;
    12. 			parent = (child - 1) / 2;
    13. 		}
    14. 		else
    15. 		{
    16. 			break;
    17. 		}
    18. 	}
    19. }

    利用上面例子给出的数值建立大堆：

    在完成了建立大堆的代码后，下面就是实现上面所说的排序。其中，调整结点位置的函数Adjustdown需要选出除根结点之外的最大结点，代码如下：

    1. void Adjustdown(HPDataType* a, int size, int parent)
    2. {
    3. 	int child = parent * 2 + 1;
    4. 	while ( child < size)
    5. 	{
    6. 		//找出较大的结点
    7. 		if (child+1 < size && a[child + 1] > a[child])
    8. 		{
    9. 			child++;
    10. 		}
    11. 		if (a[parent] < a[child])
    12. 		{
    13. 			Swap(&a[parent], &a[child]);
    14. 			parent = child;
    15. 			child = parent * 2 + 1;
    16. 		}
    17. 		else
    18. 		{
    19. 			break;
    20. 		}
    21. 	}

    对于首位结点的调整，只需要创建变量end来记录尾结点的下标，每次交换后直接让end--即可，对应代码如下：

    1. void HPqort(int* a, int n)
    2. {
    3. 	for (int i = 0; i < n; i++)
    4. 	{
    5. 		Adjustup(a, i);
    6. 	}
    7.  
    8. 	int end = n - 1;
    9. 	while (end > 0)
    10. 	{
    11. 		Swap(&a[0], &a[end]);
    12. 		Adjustdown(a, end, 0);
    13. 		end--;
    14. 	}
    15. }

    效果如下：

    3.2 降序排序：

    对于降序排序，与升序排序原理相同，但是，在实现降序排序时，需要利用小堆，而非大堆。对于代码的实现，只需要更改函数中的> ,<即可，不过多解释。

    4. 向下调整健堆以及两种建堆方法的优劣：

    4.1 向下调整建堆：

    4.1.1 向下建堆思路分析：

    在上面，提到了利用函数Adjustup，使新插入的结点不断向上调整来建堆的方法。本部分，将引入利用Adjustdown使结点不断向下调整来建堆的方法。为了方便演示原理，下面列举一个二叉树，并给出二叉树的存储结构和逻辑结构：

    存储结构如下：

    逻辑结构如下：


     按照之前向上调整建堆的整体思路，向下调整建堆，也是需要通过比较结点之间的关系，来交换结点的位置。这里给出的例子为建立一个大堆。对于结点交换的条件前面也提到，就是被调整结点的子树必须是大堆或者小堆，图中所给出的数据结构并不满足大小堆的关系，需要对结点进行调整，但是如果要对根结点进行调整，根结点的子树并不满足大堆或小堆的条件，想要对于子树的根结点进行调整，必须满足子树的子树是大、小堆。。。。。。

    为了解决上述问题，可以从树的叶子结点的父结点开始调整，因为叶子结点只有一个结点，可以看作大堆或小堆，例如存储数值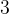32的结点，其子树都是叶子结点，可以将这两个子树都看作大堆。满足调整的条件，因此，调整需要从树中第一个非叶子结点开始调整。及存储数值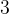32的结点，因为建立大堆，所以，如果子结点中最大的子结点大于父结点则交换，反之不变，操作一次后，需要指向上一个非叶结点。

    例如对上面的树：首先对比存储数值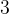32结点的子结点的大小，并进行交换：

    随后按照上面的规律，继续调整结点，即：

    继续按照上述规律对树进行调整，即：

    最后调整的效果如下：


     4.1.2 向下调整建堆代码分析：

    在上面给出相关思路后，对于代码，只需要注意循环的起始，结束条件即可。前面分析到，向下调整建堆的第一次调整是从第一个非叶结点开始的。也就是最后一个结点的父结点。这个结点的下标可以表示为：(n-1-1)/2，其中，n-1是表示最后一个结点的下标，剩下的可以由上篇文章给出的关于子、父结点的关系等式得出。结束条件，也就是最极限的情况，即：该结点调整到根结点所在的位置，此时下标为0。在确定了循环的条件后，给出代码：

    1. void HPqort(int* a, int n)
    2. {
    3.  
    4.  
    5.  
    6. 	//向下调整建堆
    7. 	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
    8. 	{
    9. 		Adjustdown(a,n,i);
    10. 	}
    11.  
    12. }
    13.  
    14. int main()
    15. {
    16. 	Test1();
    17. 	int a[] = { 2,3,5,100,70,32,50,60,7,4,6,8,65 };
    18. 	HPqort(a, sizeof(a) / sizeof(int));
    19. 	printf("\n");
    20. 	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
    21. 	{
    22. 		printf("%d ", a[i]);
    23. 	}
    24. 	return 0;
    25. }

    结果如下：

     与上面调整后堆的逻辑结构转为存储结构后与结果相同。

    4.2 两种建堆方法的优劣性分析：

    文章中虽然给出了向上调整建堆和向下调整建堆的两种方法，但是在一般运用时，都是采用向下调整建堆，原因如下：

    1. 在上面排序的代码中，同样使用了向下调整函数Adjustdown，因此，如果在建立堆时就选择向下调整建堆，则构建堆排序只需要构建向下调整函数这一个函数即可。若采用向上调整建堆的方法，则需要同时构建向上调整函数Adjustup和向下调整函数Adjustdown。较为麻烦。

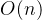    2. 采用向上调整建堆的方法的时间复杂度为O(n* logn),向下调整建堆的时间复杂度为O(n)。下面将给出证明：

    4.2.1 向下调整时间复杂度分析：

    二叉树层数与每层结点数量的关系如上图所示，从上面介绍向下调整的方法中，可以推断出每层结点最坏情况下需要向下调整的次数，树的第一层结点最坏情况下，每个结点需要调整的次数为n-1次，第二层每个结点需要调整的次数在最坏情况下为\(n-2\)次，一次向下递减，到了树的倒数第二层，最坏情况下，每个结点只需要调整一次。用\(T(n)\)表示树最坏情况下需要调整的次数总和：

    \(T(n) = 2^0*(n-1) + 2^1*(n-2) + 2^2*(n-3)+......+2^{n-2}*1\)

    对于 上式的运算，可以采用错位相减法，定义\(S(n) = 2*T(n)\)，\(S(n)\)可以表示为下式：

    \(S(n) = 2^1*(n-1) + 2^2*(n-2)+ 2^3*(n-3) + ......+ 2^{n-1}*1\)

    \(S(n)- T(n)\)可以通过下面的图表示：

    运算后可以得到结果： 

     \(S(n)- T(n)=2^{n-1} + 2^{n-2}+......+2^1-2^0*(n-1)\)

    化简后可以得到结果：

    \(T(n) = 2^n-1-n\)

    在前面的图中，可以得出树层数与结点之间关系的等式，令\(N\)为结点数，\(n\)为层数，二者的关系可以表示为：\(N = 2^{n-1}\),换算后可以得到：\(n = log_{2}(N+1)\)，因此\(T(n)\)可以进一步表示为：

                                                     \(T(N) = N- log_{2}(n+1)\)

    由上面给出的等式可得，向下调整的时间复杂度为O(n)。

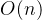    4.2.2 向上调整时间复杂度分析：

    向上调整与向下调整的不同点是，二者相同层数的结点调整次数不同：

    对于第一层结点，不需要调整，对于第二层结点，最坏的情况下每个结点需要调整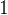1次，一次类推，第\(n\)层的结点 ，每个结点需要调整n-1次。同样，利用\(T(n)\)来表示树中结点的所有调整次数：

    \(T(n) = 2^1*1+2^2*2+2^3*3+......+2^{n-2}*(n-2)+2^{n-1}*(n-1)\)

    同样利用错位相减法计算，\(S(n) =2 *T(n)\)

    \(S(n) = 2^2*1+2^3*2+2^4*3+......+2^{n-1}*(n-2)+2^n*(n-1)\)

    \(S(n)-T(n) = (N+1)*(log_{2}(N+1)-1)+1-N\)

    通过上面的式子可以得出向上调整的时间复杂度：\(O(n*logn)\)

    5. 堆排序的时间复杂度：

    在上面的内容中，给出了堆排序的代码，即：

    1. void HPqort(int* a, int n)
    2. {
    3. 	//向下调整建堆
    4. 	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
    5. 	{
    6. 		Adjustdown(a,n,i);
    7. 	}
    8. 	//堆排序
    9. 	int end = n - 1;
    10. 	while (end > 0)
    11. 	{
    12. 		Swap(&a[0], &a[end]);
    13. 		Adjustdown(a, end, 0);
    14. 		end--;
    15. 	}
    16.  
    17. }
    18.  
    19. int main()
    20. {
    21. 	Test1();
    22. 	int a[] = { 2,3,5,100,70,32,50,60,7,4,6,8,65 };
    23. 	HPqort(a, sizeof(a) / sizeof(int));
    24. 	printf("\n");
    25. 	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
    26. 	{
    27. 		printf("%d ", a[i]);
    28. 	}
    29. 	return 0;
    30. }

    并且分析了，采用向下调整的方式进行建堆，时间复杂度为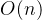O(n),在排序阶段，虽然依旧采用向下调整函数，但是需要注意，建堆采用的向下调整是针对于每一个结点的，但是在排序阶段，向下调整只是在某次循环中，针对首结点进行向下调整，最坏的情况下，调整的次数为\(logN\)(N为结点数），假设树中有\(N\)个结点，时间复杂度为\(O(N*logN)\),综合下来，堆排序的时间复杂度为\(O(N*logN)\)。

  • 相关阅读:
    直播间挂人气技术分析【简易版本】2.0
    STM32实战总结：HAL之I2C
    【AI理论学习】语言模型：掌握BERT和GPT模型
    基于 VSC 的 UPFC(统一潮流控制器）研究（Simulink）
    线上多域名实战
    <二>强弱指针使用场景之 多线程访问共享对象问题
    豫见大势，豫见智慧——第九届博博会侧记
    [云原生] 二进制k8s集群（下）部署高可用master节点
    Python特征分析重要性的常用方法
    -最低分-
  • 原文地址：https://blog.csdn.net/2301_76836325/article/details/133240418