【C语言】八大排序算法

---

1.排序的概念及其应用

1.1排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字(如价格，销量，好评率，排名等)的大小，递增或递减的排列起来的操作。
稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j],且r[i]在r[j]之前，而在排序后的序列中，依然保持此规律，则称这种排序算法是稳定的，否则称为不稳定的。
内部排序：数据元素全部放在内存中的排序。
外部排序：待排序的数据量很大，以致于内存不能一次容纳全部数据，所以在排序过程中需要对外存进行访问。
二者衡量效率的方法：内部排序：时间复杂度；外部排序：IO次数，也就是读写外存（如磁盘上的文件）的次数。

1.2排序的应用

1.3常见的排序算法

1.4时间性能的测试（测试排序算法的好坏）

1.排序OJ（可以使用多种排序算法来跑这个题）(注意有些算法会超出时间限制，如选择排序)。
2.时间性能

//测试排序函数性能(直观看出算法的好坏：通过排序的所消耗的时间)
void TestOP()
{
	srand((unsigned int)time(NULL));//生成随机数

	//带排序的数据量
	int N = 100000;
	//测试多个排序算法的方法：开辟多个相同数据的数组（动态，栈区空间可能会溢出）
	int* a1 = (int*)malloc(sizeof(int)*N);
	assert(a1);
	int* a2 = (int*)malloc(sizeof(int)*N);
	assert(a2);
	int* a3 = (int*)malloc(sizeof(int)*N);
	assert(a3);
	int* a4 = (int*)malloc(sizeof(int)*N);
	assert(a4);
	int* a5 = (int*)malloc(sizeof(int)*N);
	assert(a5);
	int* a6 = (int*)malloc(sizeof(int)*N);
	assert(a6);
	int* a7 = (int*)malloc(sizeof(int)*N);
	assert(a7);
	int* a8 = (int*)malloc(sizeof(int)*N);
	assert(a8);

	//空间开辟完后，我们开始给这些数组相同的随机数据
	for (int i = 0; i < N; i++)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
		a8[i] = a1[i];
	}
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	QuickSort1(a5, 0, N - 1);
	int end5 = clock();

	int begin5 = clock();
	QuickSort2(a5, 0, N - 1);
	int end5 = clock();

	int begin5 = clock();
	QuickSort3(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	MergeSort(a6, N);
	int end6 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort1:%d\n", end5 - begin5);
	printf("QuickSort2:%d\n", end5 - begin5);
	printf("QuickSort3:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
	free(a8);

}
int main()
{
	TestOP();
	
	return 0;
}

2.常见排序算法的实现

2.1直接插入排序

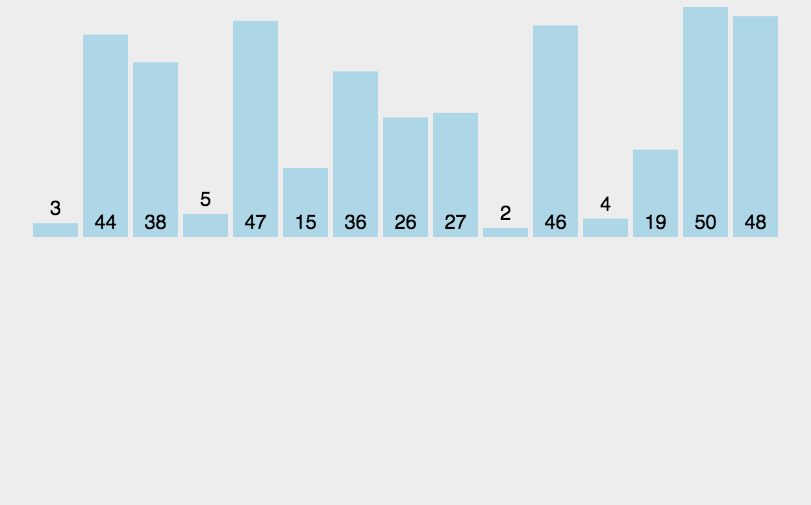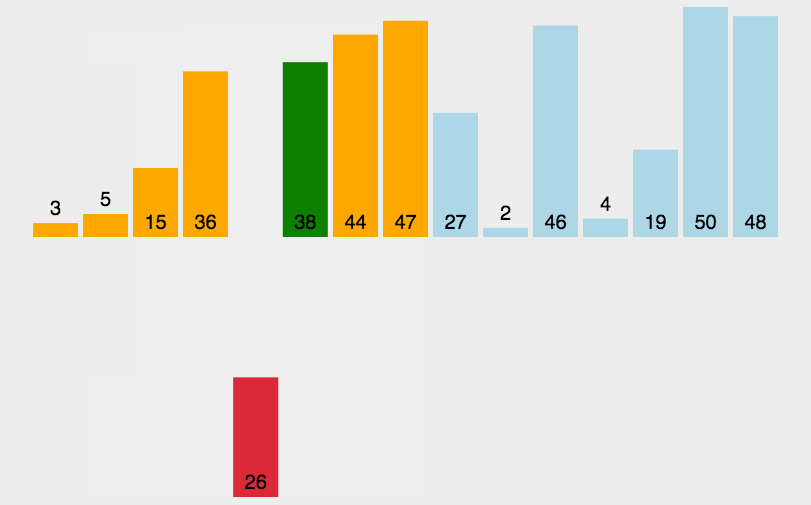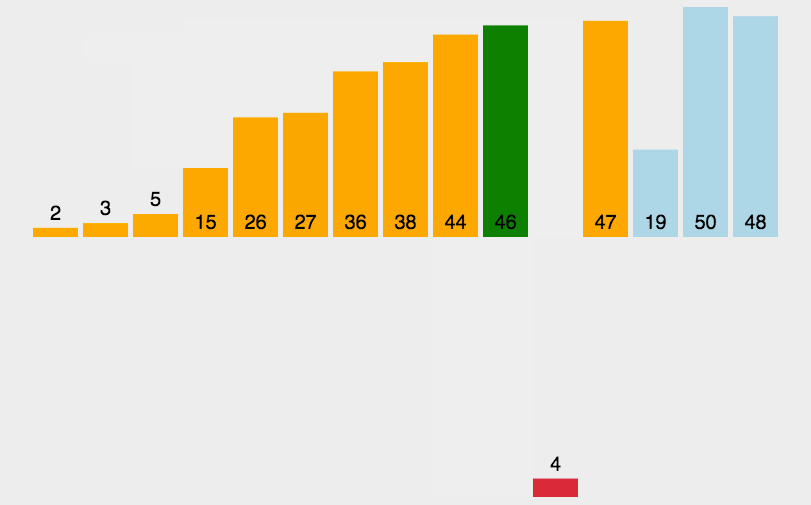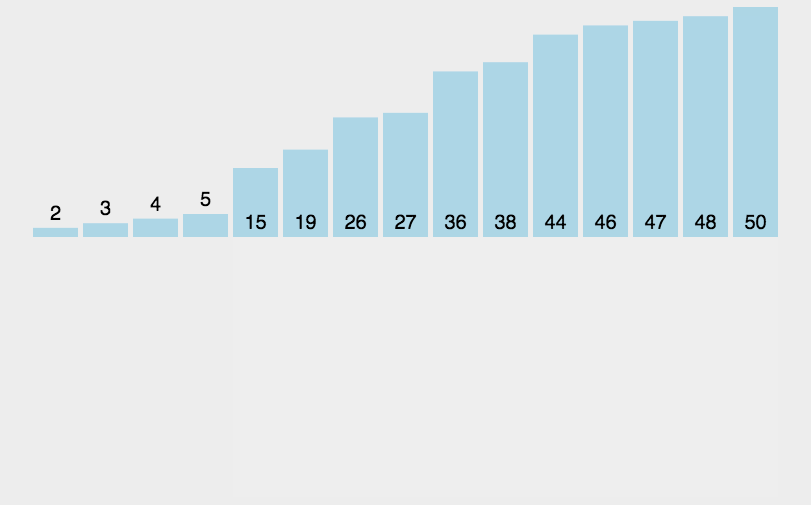
插入排序，又叫直接插入排序，我们在玩扑克牌的时候，就用到了直接插入排序的思想。在待排序的元素中，假设前n-1个元素已经有序，将第n个元素插入到前面已经排好的序列中，使得前n个元素有序。按照此思想，直到整个序列有序。但一开始的数据是随机的，所以我们不知道序列的哪个部分有序，所以一开始我们只能认为第一个元素是有序的，从第2个元素开始，依次向前面排好的序列插入。

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n-1; i++)
	{
		int end = i;
		int tmp = a[end + 1];

		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;//找到正确顺序的插入位置
			}
		}
		a[end + 1] = tmp;
	}
}

直接插入排序算法特性：
1.数据越接近有序，直接插入排序算法效率越高。
2.最坏时间复杂度:O(N^2),最好时间复杂度：O(N)。
3.空间复杂度：O(1)
4.稳定性：稳定，

2.2希尔排序

希尔排序也是插入排序，但是它是对直接插入排序的一种优化。它又称为缩小增量排序，算法思想是：
1.先预排序：先选定一个小于N的整数gap作为第一次的增量，然后将所有距离为gap的元素分在同一组，并对每一组进行直接插入排序。然后gap增量减小，作为第二增量，重复以上操作。
2.再直接插入排序：当gap增量减小到1的时候，进行一次直接插入排序，则排序完成。

问题：为什么要让gap增量从大到小呢？
原因：当代排序的数据量很大时，如果gap过小，效率就较低，gap越大数据挪动的距离就越大，gap越小，数据挪动排序的距离就越小。前期让gap较大，可以让数据更快的挪动到自己对应的位置附近，减少挪动次数。直到gap的增量为1（缩小gap：gap=gap/2或gap=gap/3+1）。

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)//gap>1预排序，gap==1直接插入排序
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

希尔排序算法特征总结：
1.平均时间复杂度：O(N^1.3)
2.空间复杂度：O(1)
3.稳定性：不稳定

2.3选择排序

选择排序，即每次从待排序的序列中选出一个最小值，然后放在序列的起始位置begin（排好一个元素之后，begin递增），直到全部待排序数据排序完成。

时间复杂度O(N^2),空间复杂度O(1)。

void SelectSort(int* a, int n)
{
	//先假设第一个元素最小
	for (int i = 0; i < n; i++)
	{
		int begin = i;
		int minindex = i;
		while (begin < n)
		{
			if (a[begin] < a[minindex])
			{
				minindex = begin;
			}
			begin++;
		}
		Swap(&a[minindex], &a[i]);
	}
}

选择排序的优化版本：
实际上，我们可以一趟选出两个值，一个最大值，一个最小值，然后将最小值放在开头，最大值放在末尾，然后left++,right–,依次继续在剩下的数据当中找最大值和最小值，这样可以使选择排序的效率快一倍。

void SelectSort2(int* a, int n)
{
	int left = 0;
	int right = n - 1;
	while (left < right)
	{
		int minindex = left;
		int maxindex = left;
		for (int i = left; i <= right; i++)
		{
			if (a[i] < a[minindex])
			{
				minindex = i;
			}
			if (a[i] > a[maxindex])
			{
				maxindex = i;
			}
		}
		Swap(&a[minindex], &a[left]);
		if (maxindex == left)
		{
			maxindex = minindex;
		}
		Swap(&a[maxindex], &a[right]);
		left++;
		right--;
	}
}

直接选择排序的特性总结：
1.直接选择排序较其它排序较好理解，但是效率比较低，实际中少用。
2.最好和最坏的时间复杂度都是O(N^2)。
3.稳定性：不稳定。

2.4堆排序

要学习堆排序，首先要学习基础的二叉树结构，学习堆的向下调整算法，使用堆排序之前，我们得先建一个堆出来，堆的向下调整算法的前提是：根节点的左右子树均是大堆或小堆。由于堆排序在向下调整的过程中，需要从孩子中选择出较大或较小的那个孩子，父亲才与孩子进行交换，所以堆排序是一种选择排序。堆排序的详解请至博客：堆排序

void AdjustDown(int* a,int n,int parent)
{
    int minchild=2*parent+1;
    while(minchild<n)
    {
        //找较大的那个孩子
        if(minchild+1<n&&a[minchild+1]>a[minchild])
        {
            minchild++;
        }
        if(a[parent]<a[minchild])
        {
            Swap(&a[parent],&a[minchild]);
            parent=minchild;
            minchild=parent*2+1;
        }
        else
        {
            break;
        }
    }
}
void HeapSort(int* a,int n)
{
    //先建堆，升序——建大堆
    for(int i=(n-1-1)/2;i>=0;i--)
    {
        AdjustDown(a,n,i);
    }
    //向下调整建堆
    int i=1;//此时最大的数据已经在堆顶
    while(i<n)
    {
        Swap(&a[0],&a[n-i]);
        AdjustDown(a,n-i,0);
        i++;
    }
}

堆排序特性总结：
1.堆排序使用堆来选数，效率较高。
2.时间复杂度：O(N*logN)。
3.空间复杂度：O(1)。
4.稳定性：不稳定。

2.5冒泡排序

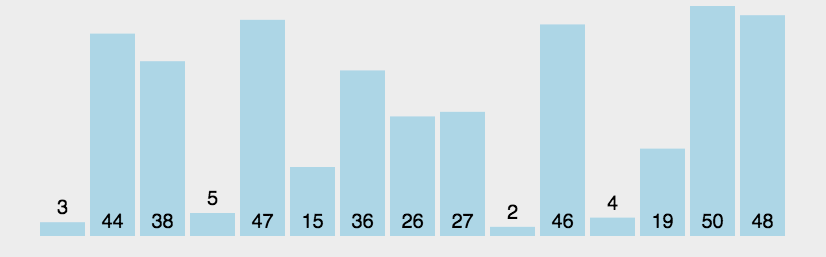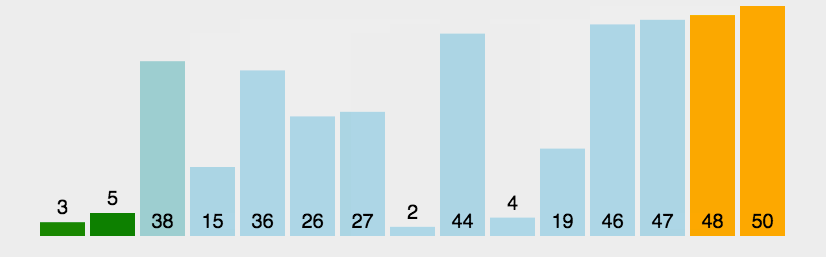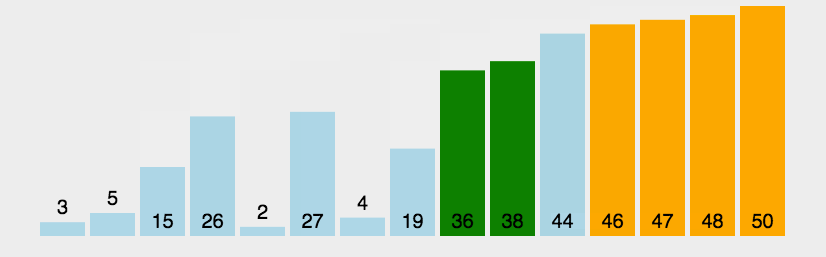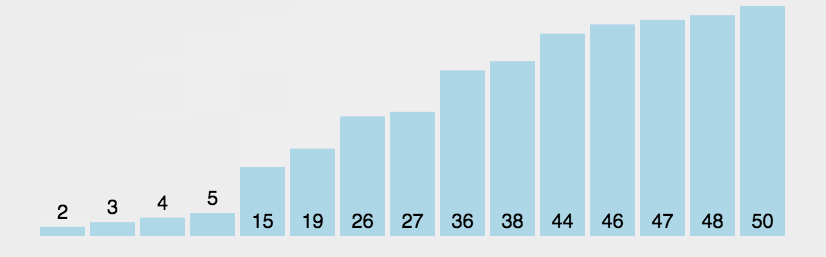
冒泡排序是一种交换排序，冒泡排序是从第一个元素开始，相邻的两个数俩俩比较，若后面一个数大于前一个数则交换，一直到把每趟的最大元素都排在末尾，所以冒泡排序是比较函数的一种。根据动图来观察，冒泡排序算法跟直接选择排序有点像，排好的元素，相对的位置之间就不再变动了。

void bubble_Sort(int* a, int n)
{
	int i = 0;
	int j = 0;
	int flag = 0;
	for (i = 0; i < n - 1; i++)//趟数
	{
		flag = 0;
		for (j = 0; j < n - 1 - i; j++)//相邻元素之间的比较次数
		{
			if (a[j + 1] < a[j])
			{
				Swap(&a[j], &a[j + 1]);
				flag = 1;
			}
		}
		if (flag == 0)
		{
			break;
		}
	}
}

冒泡排序法特性总结：
1.冒泡排序法是一种常见的排序算法。
2.最坏时间复杂度：O(N^2)，最好时间复杂度：O(N)。
3.空间复杂度:O(1)。
4.稳定性：稳定。

2.6快速排序

快速排序是公认的排序之王，快速排序是Hoare在1962年提出的一种二叉树结构的排序算法，他是一种交换排序，基本思想为:
任取待排序元素中的某元素作为基准值key，按照该基准值将带排序序列分为两个子序列，左边子序列的值都小于基准值，右边则都大于基准值，然后左右序列重复该过程（递归），直到所有元素都排列在相遇的位置上为止。

关于如何按照基准值将待排序序列分为两个子序列，常见的三种方式是：
1.Hoare版本
2.挖坑法
3.前后指针法

Hoare版本

方法：
我们先写出单趟排序PartSort(int* a,int left,int right)；因为是递归式的二叉树结构。

1.先选出一个key，一般是最左边或者最右边的。
2.定义left和right，left向右遍历序列，right向左遍历序列（如果定义最左边的那个元素为key,那么right先走，若定义最右边的那个元素为key，则left先走）。
3.在走的过程中，若R遇到小于key的数则停下，到L开始走，直到L遇到比key大的数时，L也停下，将下标为left，right的数据交换，直到L与R相撞，假设它们相遇的位置meeti，最后把a[meeti]和a[keyi]交换，返回L与R相遇的位置。
4.经过一次单趟排序，最终使得key左边的数据都小于key，右边的数据都大于key。
5.然后我们再将key的左序列和右序列再次进行这种单趟排序，每进行一次单趟排序就可以确定一个数据的排序位置，如此递归操作下去，直到最后左右序列只有一个数据或没有数据，则层层返回，此时序列就排好啦。

int PartSort1(int* a, int left, int right)
{
	int keyi = left;
	while (left < right)
	{
		while (left < right&&a[right] >= a[keyi])
		{
			right--;
		}
		while (left < right&&a[left] <= a[keyi])
		{
			left++;
		}
		if (left < right)
		{
			Swap(&a[left], &a[right]);
		}
	}
	int meeti = left;
	Swap(&a[meeti], &a[keyi]);
	return meeti;
}
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	int keyi = PartSort1(a, begin, end);

	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

快速排序的两个优化

1.小区间优化：在二叉树的结构中，最后一层的结点个数是2^(h-1),占比约50%，倒数第二层的结点个数占比约25%，倒数第三次占比约12.5%，如果我们直接使用以上的方法就会导致递归调用的层数太多了，每一层的递归次数会以2倍的形式快速增长。那么递归得太深最容易导致的问题就是——栈溢出，所以我们要对其进行优化。优化方式：设置一个判断句，当一趟中数据量长度小于等于一定数值，如8，就不再进行快速排序，转而采用直接插入排序。

问：为什么不采用希尔排序？

答：希尔排序还要进行预排序，对于数据量大的时候采用希尔排序比较合适，数量较小时，还要进行预排序，不一定就效率高。

2.优化选key逻辑:快速排序的时间复杂度是O(NlogN),这是我们在理想情况下计算的结果。在理想情况下，我们每次进行完单趟排序后，key的左右序列的长度相同（如图2）。可是谁能保证你每次选取的key都是正中间的数呢？针对有序或接近有序的序列，如果我们依然选择最左边的作为基准值，那么我们的递归深度就为N（如图1），这种情况下，快速排序的时间复杂度退化为O(N^2)。且容易导致栈溢出。

所以我们优化key的思想是：三数取中，取序列的中间值作为key，再与a[left]交换，此时定义key时，依然为left，但实际上是原序列的中间值，这就确保了我们所选取的key，不会是最大值或最小值了，所以接下来的总体逻辑不变。


时间复杂度O(N*logN)。

int GetMidIndex(int* a, int left, int right)
{
	int mid = left + (right - left) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[right] < a[left])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
int PartSort1(int* a, int left, int right)
{
	int mid = GetMidIndex(a, left, right);
	Swap(&a[left], &a[mid]);
	int keyi = left;

	while (left < right)
	{
		while (left < right&&a[right] >= a[keyi])
		{
			right--;
		}
		while (left < right&&a[left] <= a[keyi])
		{
			left++;
		}
		if (left < right)
		{
			Swap(&a[left], &a[right]);
		}
	}
	int meeti = left;
	Swap(&a[meeti], &a[keyi]);
	return meeti;
}
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}
	if (end - begin <= 8)
	{
		InsertSort(a + begin, end - begin + 1);
	}
	int keyi = PartSort1(a, begin, end);

	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

挖坑法

时间复杂度：O(N*logN)。

挖坑法的基本思想：
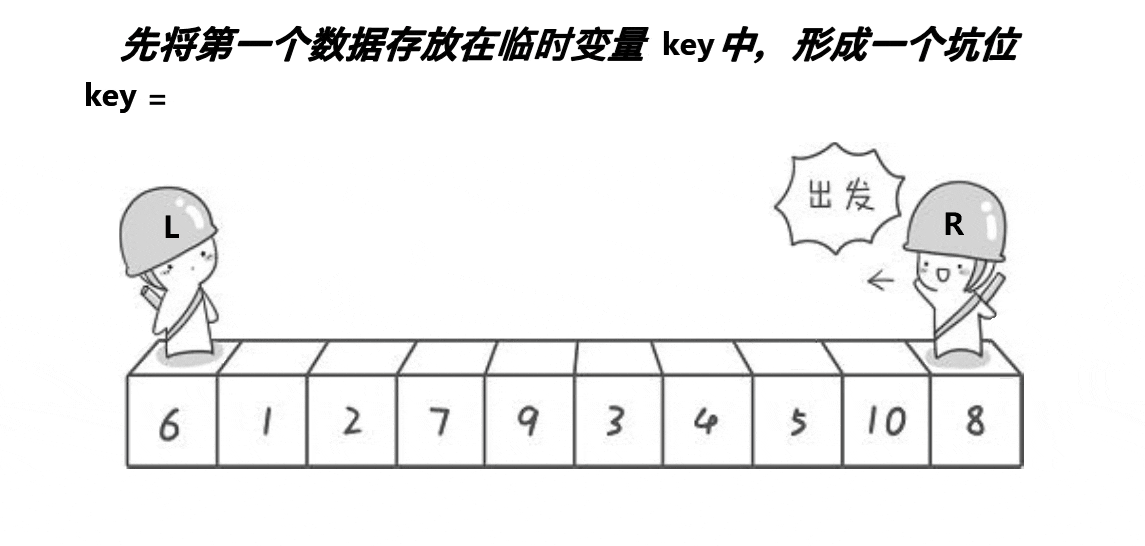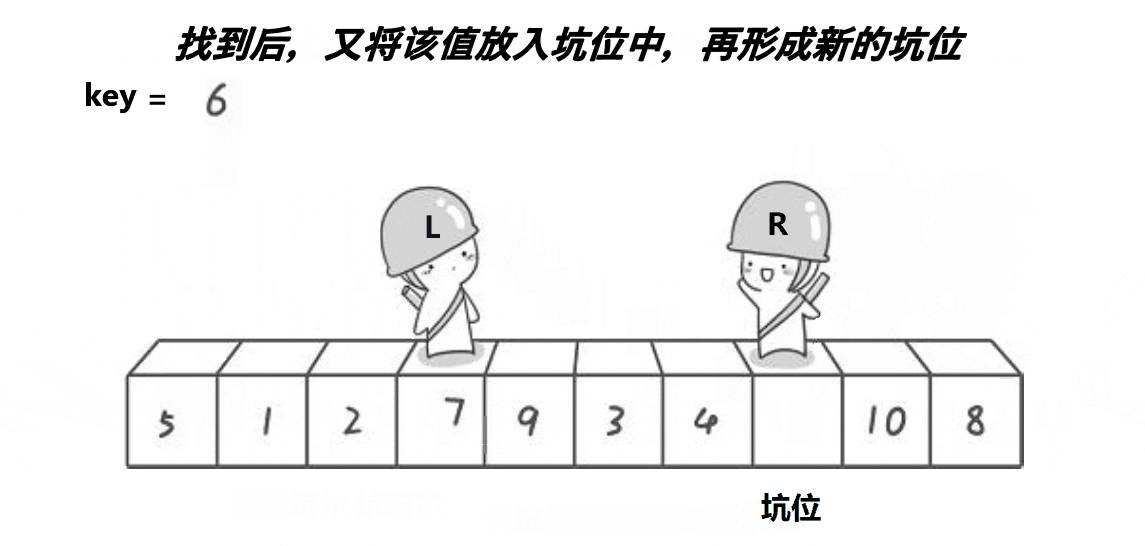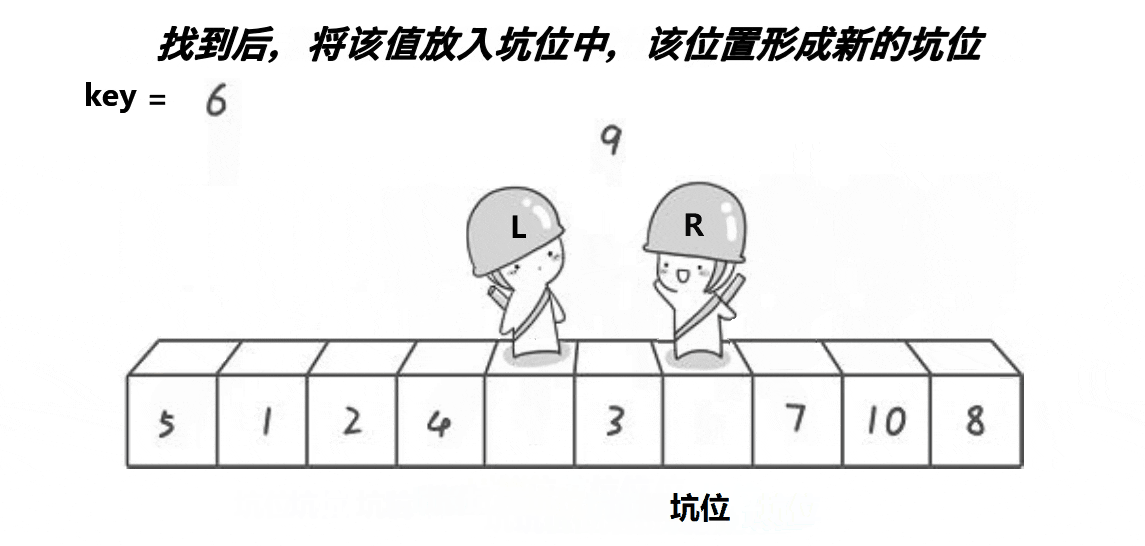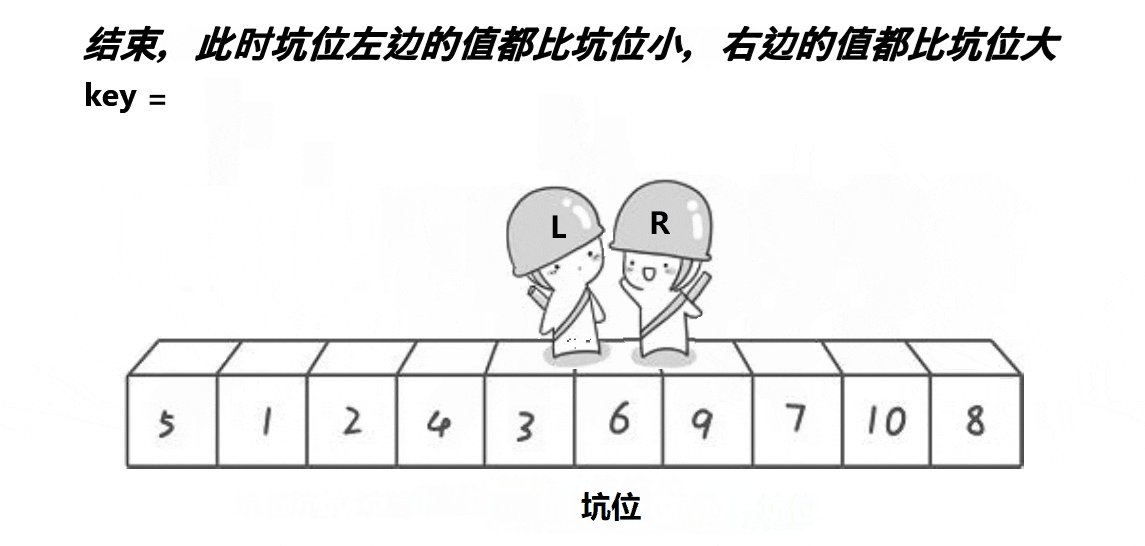
1.利用优化后的选key逻辑：三数取中， 选出key变量作为坑位，保存作为坑位的值（保存起来就可以覆盖了，就相当于坑位）。
2.定义一个L，一个R，L从左向右走，R从右向左走（若在最左边挖坑，则R先走；若在最右边挖坑，则L先走）。
3.假设我们定义最右边为坑位，在R走的过程中，若R遇到小于key的数，则将这个数抛入坑位，然后这个数原来的位置变成坑位，然后L向右走走，若遇到大于key的数则停下，将这个数抛入坑位，这个数的位置又形成新的坑位，如此循环下去，直到最终L与R相遇，最后再将key抛入最后形成的坑位。
4.经过一次单趟排序，也能使得key左边的数据都小于key，右边的数据都大于key。
5.然后也是跟Hoare法一样，key的左右子序列不断的进行单趟排序（递归），直到左右序列只有一个数据或者没有数据，便停止递归，层层返回。

int PartSort2(int* a, int left, int right)
{
	int mid = GetMidIndex(a, left, right);
	Swap(&a[mid], &a[left]);
	//1.保存坑位
	int key = a[left];
	int hole = left;
	while (left < right)
	{
		//2.挖坑
		while (left < right&&a[right] >= key)
		{
			right--;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right&&a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	//L与R相遇
	a[hole] = key;
	return hole;
}

前后指针法

时间复杂度：O(N*logN)。

前后指针法基本思想：
1.用三数取中法，选出一个key，最左边的或最右边的。
2.刚开始prev指向序列开头，cur指向prev+1的位置。
3.若cur指向的值比key小，则cur停下来，++prev，交换prev和cur位置上的数据，然后cur继续往后++，prev紧跟cur，但若cur指向的数据大于等于key，则cur继续++，但prev不动，如此规律进行下去，直到cur越界，跳出循环，最后将prev指向的数据和keyi指向的数据交换即可。
4.经过一次单趟排序，也能使得key左边的数据都小于key，右边的数据都大于key。
5.然后也是跟Hoare法一样，key的左右子序列不断的进行单趟排序（递归），直到左右序列只有一个数据或者没有数据，便停止递归，层层返回。

int PartSort3(int* a, int left, int right)
{
	int mid = GetMidIndex(a, left, right);
	Swap(&a[left], &a[mid]);
	int keyi = left;

	int prev = left;
	int cur = prev + 1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi]&&++prev!=cur)
		{
			Swap(&a[prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[keyi], &a[prev]);
	return prev;
}

非递归实现快速排序

基本思想：我们学过的递归改非递归的算法，如斐波那契数列呀，n的k次方等，它们都是利用while循环，或for循环实现的非递归，思想比较简单。那么我们进入正题， 要将一个递归实现的快速排序算法改为非递归时，一般需要先模拟一个栈出来，还要清楚递归调用函数栈帧时，调用的数据，或区间的先后。注意栈是后进先出的，所以我们就利用压栈，出栈这两个功能去模拟递归的思想。

//非递归实现快速排序算法
//注意栈是：后进先出
void QuickSort(int* a, int begin, int end)
{
	ST st;
	StackInit(&st);

	//先压左数据，再压右数据
	StackPush(&st, begin);
	StackPush(&st, end);

	while (!StackEmpty(&st))
	{
		//先取右数据（因为后压的右数据，所以栈顶元素此时是右数据）
		int right = StackTop(&st);
		StackPop(&st);
		//再拿左数据
		int left = StackTop(&st);
		StackPop(&st);

		//这也是终止“递归”的一种方式
		/*if (left >= right)
		{
			continue;
		}*/

		int keyi = PartSort3(a, left, right);

		//先压keyi的右区间，再压左区间
		//这样才能符合先递归左区间，再递归右区间

		//只剩下一个数据的数据就没必要压入了
		if(keyi + 1 < right)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, right);
		}
		if(keyi - 1>left)
		{
			StackPush(&st, left);
			StackPush(&st, keyi-1);
		}
	}
	StackDestroy(&st);
}

快速排序特性总结：
1.时间复杂度:O(NlogN)。（h=logN层，每层需要遍历每个元素）
2.空间复杂度：O(logN)。
3.稳定性：不稳定

2.7归并排序

递归实现

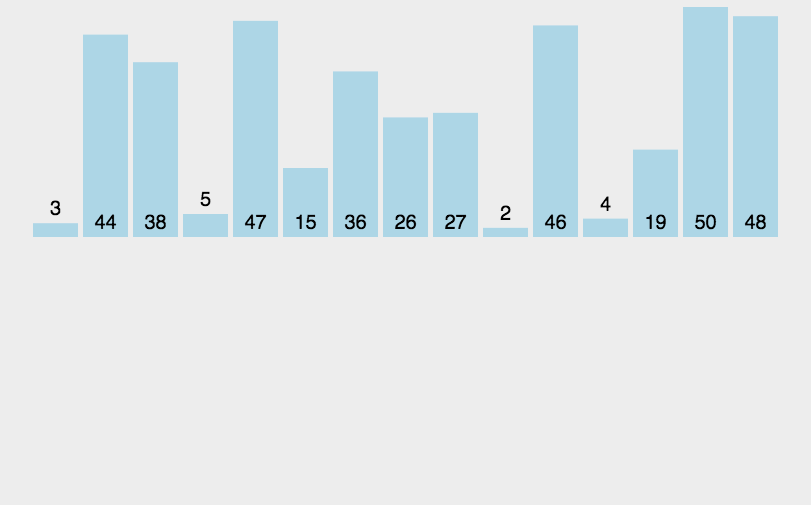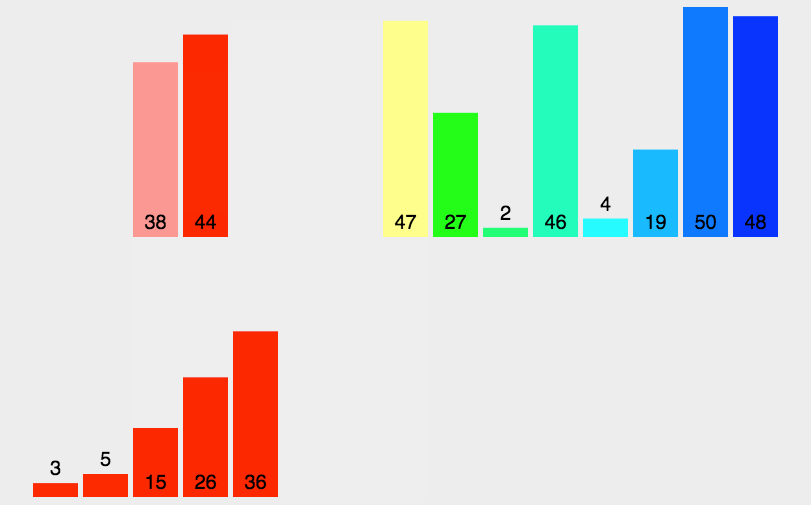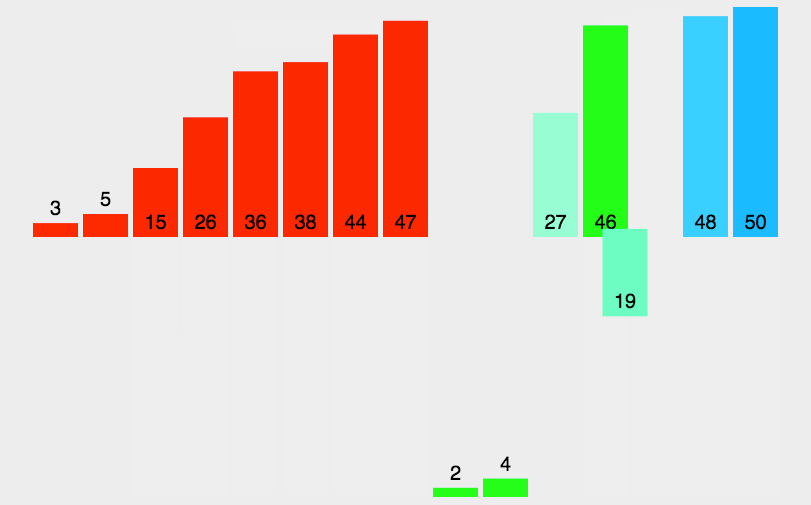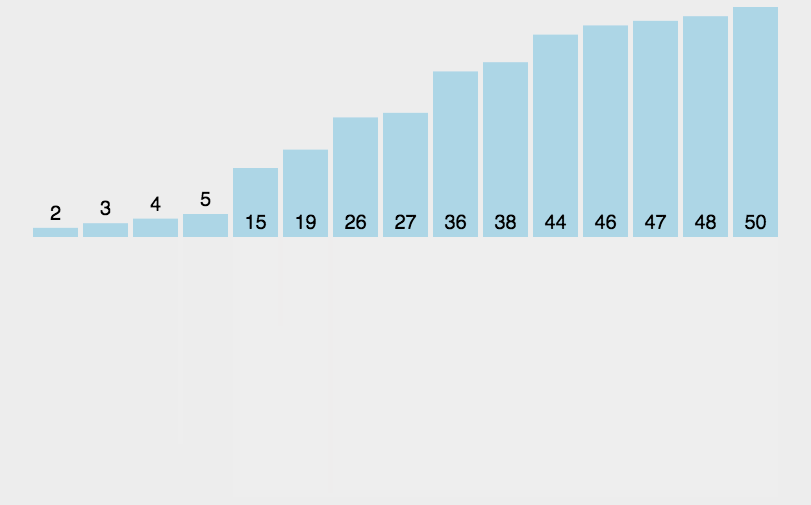
归并排序的基本思想：
类似一棵二叉树的后序遍历，先遍历左右子树，再遍历根。即先排序左右的子序列，最后才排序根部的序列。归并排序对序列的元素先进行逐层折半分组，直到递归到一个序列中只有一个元素的时候，才开始返回到上层函数，然后从最小的分组开始归并排序，因为我们额外开辟了N个空间，所以取小的尾插，和并层一个有序序列，逐层向上进行归并排序，最终所有的元素都是有序的。

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	//递归到最底层，序列中只有一个元素的时候返回
	//返回到上一层，开始进行归并排序
	if (begin >= end)
	{
		return;
	}
	int mid = begin + (end - begin) / 2;
	// [begin, mid] [mid+1, end]
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid+1, end, tmp);

	//开始进行归并排序,取小的元素尾插到tmp的对应位置
	// [begin, mid] [mid+1, end]
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;

	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	//将排序完的，拷贝到原数组的对应位置
	//归并哪部分就拷贝哪部分
	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
	//归并排序需要额外开辟n个空间,以空间换时间
	//空间复杂度为O(N)
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	//子函数实现归并排序
	_MergeSort(a, 0, n - 1, tmp);

	free(tmp);
	tmp = NULL;
}

归并排序特性总结：
1.归并排序算法每次将序列折半分组，这个的时间复杂度就为O(logN),又因为每一层都要对两组序列进行遍历比较，从而完成一次归并排序，所以这里的时间复杂度为O(N),合起来，归并排序的时间复杂度就为O(NlogN)。
2.归并排序是以空间换取时间，需要开辟额外的空间，空间复杂度为O(N)。
3.稳定性：稳定。

非递归实现

//归并排序（子函数）
void _MergeSortNonR(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{
	int j = begin1;
	//将两段子区间进行归并，归并结果放在tmp中
	int i = begin1;
	while (begin1 <= end1&&begin2 <= end2)
	{
		//将较小的数据优先放入tmp
		if (a[begin1] < a[begin2])
			tmp[i++] = a[begin1++];
		else
			tmp[i++] = a[begin2++];
	}
	//当遍历完其中一个区间，将另一个区间剩余的数据直接放到tmp的后面
	while (begin1 <= end1)
		tmp[i++] = a[begin1++];
	while (begin2 <= end2)
		tmp[i++] = a[begin2++];
	//归并完后，拷贝回原数组
	for (; j <= end2; j++)
		a[j] = tmp[j];
}
//归并排序（主体函数）
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与待排序列大小相同的空间，用于辅助合并序列
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	int gap = 1;//需合并的子序列中元素的个数
	while (gap < n)
	{
		int i = 0;
		for (i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			if (begin2 >= n)//最后一组的第二个小区间不存在或是第一个小区间不够gap个，此时不需要对该小组进行合并
				break;
			if (end2 >= n)//最后一组的第二个小区间不够gap个，则第二个小区间的后界变为数组的后界
				end2 = n - 1;
			_MergeSortNonR(a, tmp, begin1, end1, begin2, end2);//合并两个有序序列
		}
		gap = 2 * gap;//下一趟需合并的子序列中元素的个数翻倍
	}
	free(tmp);//释放空间
}

2.8外排序

首先，我们得清楚什么是内排序，什么是外排序。

内排序：数据量相对较少，可以存放到内存中进行排序。
外排序：数据量较大时，由于内存的空间比磁盘小很多，数据就只能存放到磁盘文件中。

上面介绍的算法都是在内存中进行的，那么当我们面对大量的数据时，我们可以采用归并排序。下面解析如何用归并排序实现外排序。

1.一开始，大量的数据存储在磁盘上的一个文件当中，我们将其分割成能储存进内存的大小，假设代码中的待排序的数据量是100个，那么我们每次从中读取10个数据到内存中，进行内排序，然后再将排序结果创建并写到第一个文件中，然后再继续读取接下来的10个数据，写到第二个文件中，最终会生成10个各自有序的小文件（1,2…10）
2.然后我们再对这10个小文件进行归并排序（利用文件的输入输出函数，从两个文件中各读取一个数据，然后进行比较，将较小的数据写入到一个新文件中去，然后再读取，再比较，再写入），最后就归并成了一个有序文件了。

//将file1文件和file2文件中的数据归并到mfile文件中
void _MergeFile(const char* file1, const char* file2, const char* mfile)
{
	FILE* fout1 = fopen(file1, "r");//打开file1文件
	if (fout1 == NULL)
	{
		printf("打开文件夹\n");
		exit(-1);
	}

	FILE* fout2 = fopen(file2, "r");//打开file2文件
	if (fout2 == NULL)
	{
		printf("打开文件夹失败\n");
		exit(-1);
	}

	FILE* fin = fopen(mfile, "w");//打开mfile文件
	if (fin == NULL)
	{
		printf("打开文件失败\n");
		exit(-1);
	}
	int num1, num2;
	int ret1 = fscanf(fout1, "%d\n", &num1);//读取file1文件中的数据
	int ret2 = fscanf(fout2, "%d\n", &num2);//读取file2文件中的数据

	while (ret1 != EOF && ret2 != EOF)
	{
		//将读取到的较小值写入到mfile文件中，继续从file1和file2中读取数据进行比较
		if (num1 < num2)
		{
			fprintf(fin, "%d\n", num1);
			ret1 = fscanf(fout1, "%d\n", &num1);//继续读取文件1的下一个数据
		}
		else
		{
			fprintf(fin, "%d\n", num2);
			ret2 = fscanf(fout2, "%d\n", &num2);
		}
	}
	//将file1文件中未读取完的数据写入文件mfile中
	while (ret1 != EOF)
	{
		fprintf(fin, "%d\n", num1);
		ret1 = fscanf(fout1, "%d\n", &num1);
	}
	while (ret2 != EOF)
	{
		fprintf(fin, "%d\n", num2);
		ret2 = fscanf(fout2, "%d\n", &num2);
	}
	fclose(fout1);
	fclose(fout2);
	fclose(fin);
}
//将文件中的数据进行排序
void MergeSortFile(const char* file)//文件名不允许被修改
{
	FILE* fout = fopen(file, "r");//以读的形式打开文件名为"Sort.txt"的文件
	if (fout == NULL)
	{
		printf("打开文件失败\n");
		exit(-1);
	}
	//假设文件中待排序的数据有100个，我们将其分成10份，将每份读入内存中，
	//然后进行排序，内存排序之后再写入小文件中
	int n = 10;//一次读取10个数据进行内排序
	int a[10];//读取的数据放到数组中，准备进行内排序
	int i = 0;
	int num = 0;//读取的每个数据
	char subfile[20];//文件名
	int filei = 1;//存储第i组内排序后的数据的文件名

	memset(a, 0, sizeof(int)*n);//将数组a的空间置0
	while (fscanf(fout, "%d\n", &num) != EOF)
	{
		if (i < n - 1)//先读取前9个数据
		{
			a[i++] = num;
		}
		else
		{
			//读取第10个数据
			a[i] = num;
			QuickSort(a, 0, n - 1);//将这10个数据进行快速排序

			sprintf(subfile, "%d",filei++);//将储存第i组内排序后的数据的文件的文件名
			//例如，第一个内排序完的小文件，就被命名为1，问：subfile是一个字符数组，和文件名有何关系？
			FILE* fin = fopen(subfile, "w");//创建并打开文件名为subfile的文件
			//即，第一次循环，我们打开的是文件名为1的文件，这个文件里即将要存的是第一批内排序完的10个数据
			if (fin == NULL)
			{
				printf("打开文件失败\n");
				exit(-1);
			}
			//将内排序好的10个数据写入到subfile文件中
			for (int i = 0; i < n; i++)
			{
				fprintf(fin, "%d\n", a[i]);
			}
			//完成内排序的一个小文件
			fclose(fin);

			i = 0;
			memset(a, 0, sizeof(int)*n);//将数组内存置0，准备再次读取10个数据进行内排序
		}
	}
	//归并文件，实现整体有序
	char mfile[100] = "12";//归并后文件的文件名
	char file1[100] = "1";//待归并的第一个文件的文件名
	char file2[100] = "2";//待归并的第二个文件的文件名
	for (int i = 2; i < n; i++)
	{
		//将file1文件和file2文件中的数据归并到mfile文件中
		_MergeFile(file1, file2, mfile);

		strcpy(file1, mfile);//下一次待归并的文件file1，就是上一次归并好的文件
		//更新文件名
		sprintf(file2, "%d", i + 1);//i为3，就是下一次待归并的第二个文件
		sprintf(mfile, "%s%d", mfile, i + 1);//下一次归并完的文件名为"123"，第一次归并的文件名为"12"
	}

	fclose(fout);
}
//主函数
int main()
{
	MergeSortFile("Sort.txt");//Sort.txt是待排序文件的文件名，传过去的是：字符串首元素的地址，将文件名传给函数
	return 0;
}

2.9计数排序

计数排序，又叫非比较排序，又称为鸽巢原理，是对哈希直接定址法的变形应用。它是通过统计数组中元素出现的次数，再通过统计结果将序列回收到原来的序列中。基本思想如图：

上述的方法，为绝对映射。那么当数据量较大时，如1010 1016 1010 1018 3000这样的数据进行排序，难道我们要额外开辟3031个整型空间吗？这样的话，空间的利用率就不高了。所以若是使用计数排序，我们应该使用相对映射，简单来说，就是数组中的最小值就对应count数组中的0下标，最大值对应count数组最后一个下标。这样对于这个数据，我们就只需要开辟3031-1010+1个空间了。
注意：计数排序只适用于数据范围较集中的序列进行排序，如果待排序序列较分散，则会导致空间浪费，并且计数排序只适用于整型排序。

//计数排序
void CountSort(int* a, int n)
{
	int min = a[0];//记录数组中的最小值
	int max = a[0];//记录数组中的最大值
	for (int i = 0; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];
		if (a[i] > max)
			max = a[i];
	}
	int range = max - min + 1;//min和max之间的自然数个数（包括min和max本身）
	int* count = (int*)calloc(range, sizeof(int));//开辟可储存range个整型的内存空间，并将内存空间置0
	if (count == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	//统计相同元素出现次数（相对映射）
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}
	int i = 0;
	//根据统计结果将序列回收到原来的序列中
	for (int j = 0; j < range; j++)
	{
		while (count[j]--)
		{
			a[i++] = j + min;
		}
	}
	free(count);//释放空间
}

计数排序特性总结：
1.时间复杂度：O(N+range)。
2.空间复杂度：O(range)。
3.稳定性：稳定

3.排序算法时间空间复杂度即稳定性总结