-
Pinsker 不等式证明(Proof of Pinsker‘s Inequality)
防盗:https://blog.csdn.net/qq_21149391/article/details/126844824?spm=1001.2014.3001.5502
1. Statement:
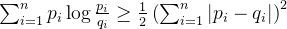
其中, 不等号左侧等价于
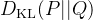 , 关于 KL散度可以看这篇介绍: KL Divergence 与 JS Divergence.
, 关于 KL散度可以看这篇介绍: KL Divergence 与 JS Divergence.不等号右侧等价于
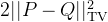 , 其中
, 其中 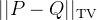 是分布PQ之间的Total Variation Distance, 记为 TV 距离, 关于 TV 距离可以看这篇的介绍: Total Variation Distance 总变差 - 知乎
是分布PQ之间的Total Variation Distance, 记为 TV 距离, 关于 TV 距离可以看这篇的介绍: Total Variation Distance 总变差 - 知乎需要注意的是不等式右侧的常数
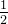 : 当 KL 散度中的 log 是以 e 为底时, 这个常数为
: 当 KL 散度中的 log 是以 e 为底时, 这个常数为 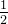 ; 当 KL 散度中的 log 是以 2 为底时, 这个常数为
; 当 KL 散度中的 log 是以 2 为底时, 这个常数为  , 所以我们在网上会看到不同形式的 Pinsker’s Inequality.
, 所以我们在网上会看到不同形式的 Pinsker’s Inequality.2. 证明:
首先给出2.1的结论, 然后使用这个结论进行证明
2.1 KL散度的链式法则(Chain rule for KL divergence)
如果
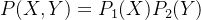 ,
, 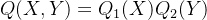 , 那么有
, 那么有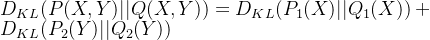
.
2.2 证明
Pinsker 定理等价于:
P, Q 是定义在 universe U 上的两个分布, 那么
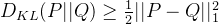
证明:
1) a special case
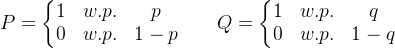
假设
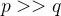 , 令
, 令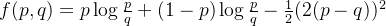
当
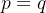 时,
时, 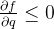 , 且
, 且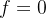 , 所以当
, 所以当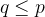 , 有
, 有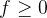
2) a general case
令
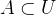 , 且
, 且 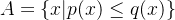 , 且:
, 且: 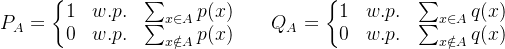
那么:
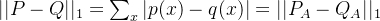
---- (1).
定义一个随机变量 Z, 且 Z 满足:
有:
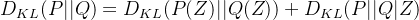
因为:
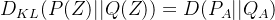
且
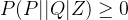
结合(1)和special case有:
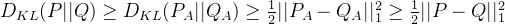
-
相关阅读:
Go语言进阶,并发通道机制搭建一个可注册昵称的聊天室
R语言中实现马尔可夫链蒙特卡罗MCMC模型
Vue(模板语法1)
【纠错】遗传算法求解VRP计算车辆容量限制的代码有bug
【运维小知识】(一)——centos系统安装(小白入门级)
Java生成SSL证书
【数据恢复篇】浅谈FTK Imager数据恢复功能
线上Timeout waiting for connection from pool问题分析和解决方案
C++ 实现运算符重载
ABAP 导入Excel表示例程序
- 原文地址:https://blog.csdn.net/qq_21149391/article/details/126844824