-
【CSAPP】计算机系统知识点笔记(新国立NUS课程,中文版)
文章目录
- 1. 数值系统 `Number System`
- 1.1 数据表示方式 `Data Representation`
- 1.2 十进制数值系统 `Decimal (base 10) `
- 1.3 其他进制的数值系统 `Other Number Systems`
- 1.4 R进制转为十进制 `Base-R to Decimal Conversion`
- 1.5 十进制转为二进制 `Decimal to Binary Conversion`
- 1.6 十进制和其他进制间的转换 `Conversion Between Decimal and Other Bases`
- 1.7 在不同进制之间的转换方法 `Conversion Between Bases`
- 1.8 二进制转换为八进制/十六进制 `Binary to Octal/Hexadecimal Conversion`
- 1.9 ASCII 码
- 1.10 负数表示方式
- 1.11 实数表示方式
- 2. MIPS I 基础
- 3. MIPS II 进阶
- 4. MIPS III 指令格式
- 5. 数据路径设计 `DataPath Design`
- 5.1 建立一个处理器:数据路径和控制 `Building a Processor: Datapath & Control`
- 5.2 MIPS处理器的实现 `MIPS Processor: Implementation`
- 5.3 基础指令处理循环 `Instruction Execution Cycle (Basic)`
- 5.4 MIPS指令执行 `MIPS Instruction Execution`
- 5.5 构造一个MIPS处理器 `Build a MIPS Processor`
- 5.6 完整的数据路径 `The Complete Datapath`
- 6. 处理器控制 `Processor Control`
- 7. 流水线 Pipelining
- 8. Caches
本笔记只是以下课程的讲义【翻译版】!持续更新中。。
原课程:National University of Singapore, IT5002 Computer Systems and Apllication, Prof. Colin Tan
可视化网站: 指令操作可视化网站1. 数值系统
Number System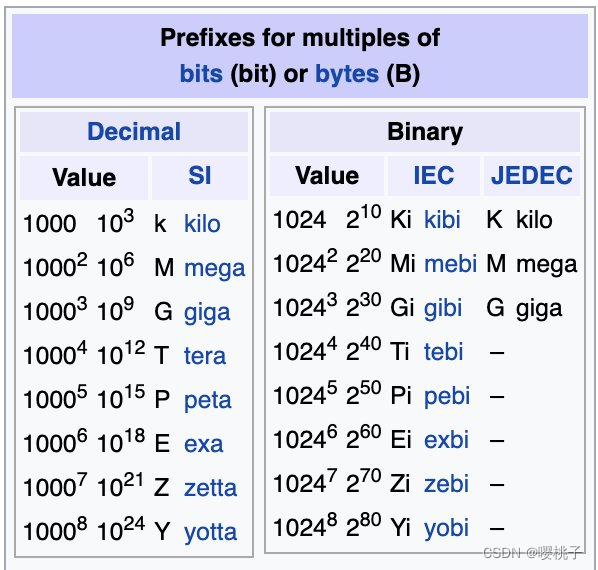
1.1 数据表示方式
Data RepresentationC语言里基本的数据类型:
int, float, double, char
(变体:short, long)数据是由一串比特数组成的(0/1)。
同一串二进制数,数据类型不同,代表着不同含义:
01000110:作为int,他是70;作为char,他是’F’单位
- 比特
bit:[b]inary dig[it]s - 字节
Byte:8 bits - 点
Nibble:4 bits(不怎么用) - 字
Word:多个bytes(可以是1 bytes, 2 bytes,4 bytes,etc. ),取决于所在计算机的架构方式
N bits可以表示最多 2 n 2^n 2n个数字 ,例如,2bits可以表示最多4个数字(00 01 10 11).
所以,如果需要表示M个数字,至少需要 ⌈ l o g 2 M ⌉ \lceil log_2M \rceil ⌈log2M⌉个bits。 例如,32个数字需要5位比特来表示,1000个数字需要10位比特来表示1.2 十进制数值系统
Decimal (base 10)十进制数值系统是一个加权位置数值系统
weighted-positional number system,他的基底是10(base / radix)。
符号Sysbols/digits: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} 0,1,2,3,4,5,6,7,8,9
每个位置上都有对应的权重: w e i g h t = 1 0 n weight = 10^{n} weight=10n
例如:
( 7594.36 ) 1 0 = ( 7 × 1 0 3 ) + ( 5 × 1 0 2 ) + ( 9 × 1 0 1 ) + ( 4 × 1 0 0 ) + ( 3 × 1 0 − 1 ) + ( 6 × 1 0 − 2 ) (7594.36)_10 = (7 × 10^3) + (5 × 10^2) + (9 × 10^1) + (4 × 10^0) + (3 × 10^{-1}) + (6 × 10^{-2}) (7594.36)10=(7×103)+(5×102)+(9×101)+(4×100)+(3×10−1)+(6×10−2)权重,10的k次幂,k =
n , n − 1 , . . . , 0 , 小数点 − 1 , − 2 , . . . , − m n, n-1, ..., 0, 小数点 -1, -2, ..., -m n,n−1,...,0,小数点−1,−2,...,−m
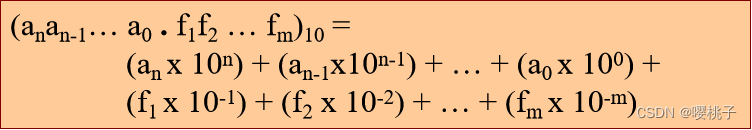
1.3 其他进制的数值系统
Other Number Systems在一些编程语言里,我们会使用特殊的标记来表明某个数字的基数:
- 在C语言里
- 八进制前面会加个0( 032 − > ( 32 ) 8 032 -> (32)_8 032−>(32)8)
- 十六进制前面会加上0x ( 0 x 32 − > ( 32 ) 16 0x32 -> (32)_{16} 0x32−>(32)16)
- 在QTSpim(一种MIPS模拟器)里
- 十六进制前面会加上0x ( 0 x 32 − > ( 32 ) 16 0x32 -> (32)_{16} 0x32−>(32)16)
- 在Verilog里
8'b11110000表示一个八位二进制数111100008'hF0表示一个八位二进制数,其值为十六进制下的F08'd240表示一个八位二进制数,其值为十进制下的240
1.4 R进制转为十进制
Base-R to Decimal Conversion直接每一位乘以对应位置的权重 i ∗ R n i * R^n i∗Rn

1.5 十进制转为二进制
Decimal to Binary Conversion- 对于整数:使用辗转相除法不断除以2,逆序取余数
- 对于小数:使用辗转相乘法不断乘以2,正序取整数
例如:
(1)整数
方法一:
要将整数转换为二进制,连续除以 2 直到商为 0。余数形成答案,第一个余数作为最低有效位 (LSB),最后一个余数作为最高有效位 (MSB) -》从下往上读余数。43
43=(101011)B 43/2=21======余1 21/2=10======余1 10/2=5=======余0 5/2=2========余1 2/2=1========余0 1/2=0========余1 从下往上读余数- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
255
255=(11111111)B 255/2=127=====余1 127/2=63======余1 63/2=31=======余1 31/2=15=======余1 15/2=7========余1 7/2=3=========余1 3/2=1=========余1 1/2=0=========余1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
方法二:
255 = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 第 7 6 5 4 3 2 1 0 位为1 = 11111111- 1
- 2
- 3
(2)小数
要将小数转换为二进制,重复乘以 2,直到小数积为 0(或直到所需的小数位数)。 进位数字或进位产生答案,第一个进位作为 MSB,最后一个作为 LSB -》 从上往下读取出来的整数部分。如:0.625=(0.101)B
0.625*2=1.25======取出整数部分1 0.25*2=0.5========取出整数部分0 0.5*2=1==========取出整数部分1- 1
- 2
- 3
再如:0.7=(0.1 0110 0110…)B
0.7*2=1.4========取出整数部分1 0.4*2=0.8========取出整数部分0 0.8*2=1.6========取出整数部分1 0.6*2=1.2========取出整数部分1 0.2*2=0.4========取出整数部分0 0.4*2=0.8========取出整数部分0 0.8*2=1.6========取出整数部分1 0.6*2=1.2========取出整数部分1 0.2*2=0.4========取出整数部分0- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
1.6 十进制和其他进制间的转换
Conversion Between Decimal and Other Bases类比1.5中十进制转换为二进制的方式:
- 对于整数:使用辗转相除法不断除以2,逆序取余数
- 对于小数:使用辗转相乘法不断乘以2,正序取整数
我们可以推导到十进制转换为R进制的方式为:
- 对于整数:使用辗转相除法不断除以R,逆序取余数
- 对于小数:使用辗转相乘法不断乘以R,正序取整数
1.7 在不同进制之间的转换方法
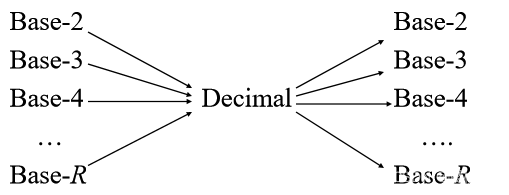
Conversion Between Basesm进制转换为n进制的通用方法:先将m进制转换为十进制(每位乘以权重,求和),再将该十进制数转换为n进制(辗转相除/乘)
1.8 二进制转换为八进制/十六进制
Binary to Octal/Hexadecimal Conversion2/8/16进制之间的相互转换有捷径:
二进制转八进制:每三位为一组换算 (10 111 011 001 . 101 110)_2 -> (2731.56)_8 2 7 3 1 . 5 6 八进制转二进制:每一位转成三位二进制数 (2731.56)_8 -> (10 111 011 001 . 101 110)_2 二进制转十六进制:每四位为一组换算 (101 1101 1001 . 1011 1000)_2 -> (5D9.B8)_16 5 D 9 B 8 十六进制转二进制:每一位转成四位二进制数 (5D9.B8)_16 -> (101 1101 1001 . 1011 1000)_2- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
1.9 ASCII 码
ASCII 码和 Unicode 用于表示字符(‘a’、‘C’、‘?’、‘\0’等)
ASCII- 美国标准信息交换码
American Standard Code for Information Interchange - 7 位(共128个, 0-127),外加 1 个奇偶校验位(奇校验或偶校验)
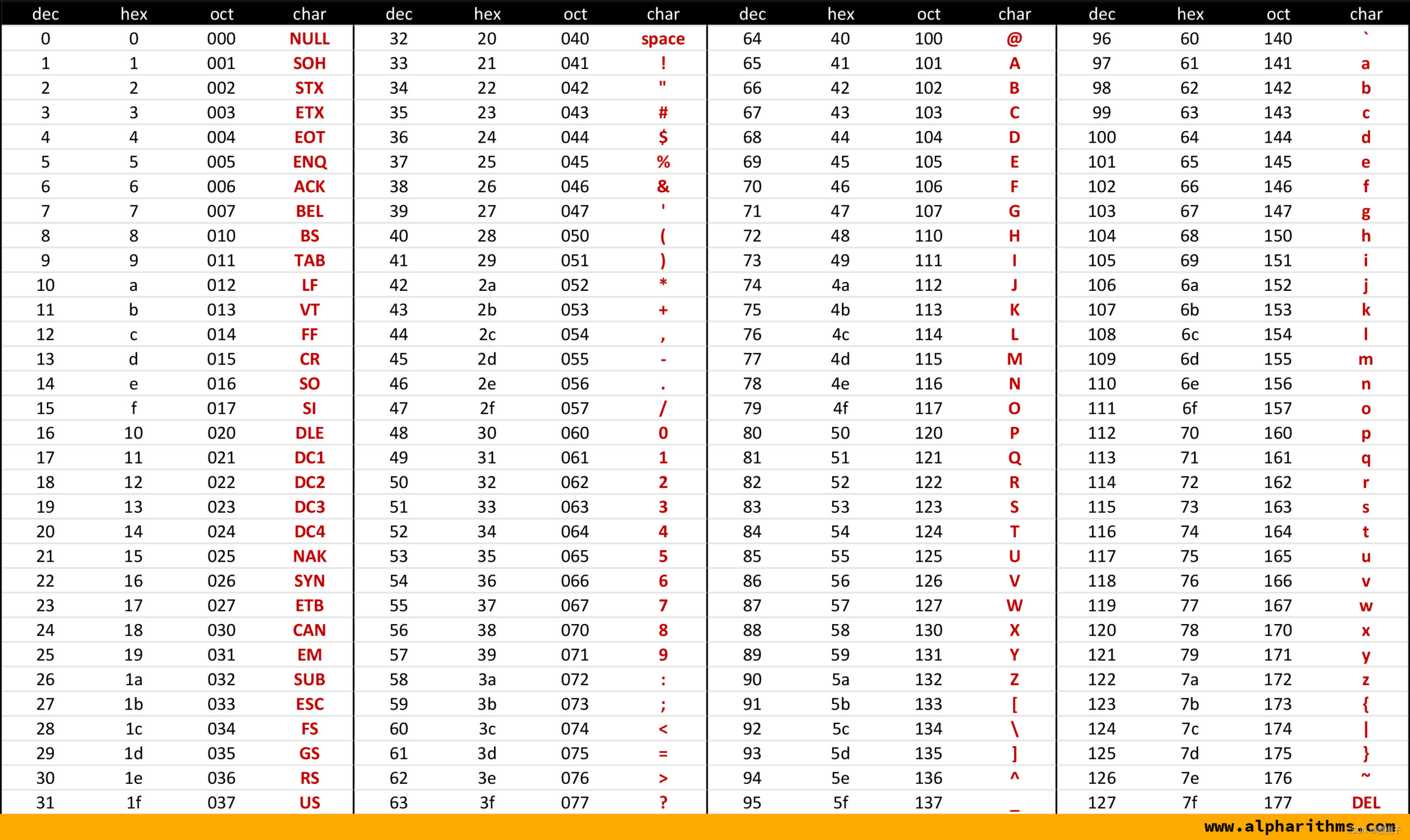
所以整数0-127和字符在C语言里是可以互相转换的。
int num = 65; char ch = 'F'; printf("num (in %%d) = %d\n", num); printf("num (in %%c) = %c\n", num); printf("\n"); printf("ch (in %%c) = %c\n", ch); printf("ch (in %%d) = %d\n", ch);- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
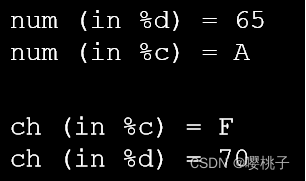
例题
int i, n = 2147483640; for (i=1; i<=10; i++) { n = n + 1; } printf("n = %d\n", n);- 1
- 2
- 3
- 4
- 5
问以上代码的输出是什么?->
-2147483646
因为C语言里int的范围是-2147483648~+2147483647
当超过2147483647时,再往上加,符号位会变为1,此时会变成负数,即-2147483648,继续加2,得到-2147483646附:其他数据类型范围参考
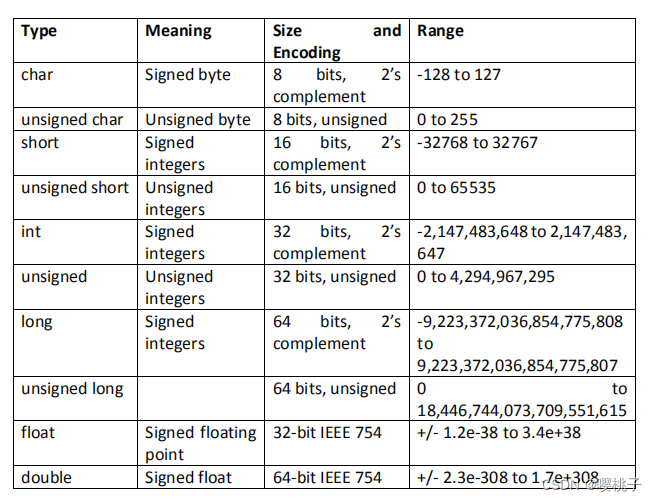
1.10 负数表示方式
- 无符号数:只有非负数值
- 有符号数:包括所有数值(正数/负数)
- 目前有三种有符号数的表示方式:
Sign-and-Magnitude- 第一类补数方式
1s Complement - 第二类补数方式
2s Complement
(1) 符号+大小
Sign and Magnitude符号由符号位上的数字表示,符号位上为1表示负数,0表示正数。
例如,1比特的符号+7比特的数值
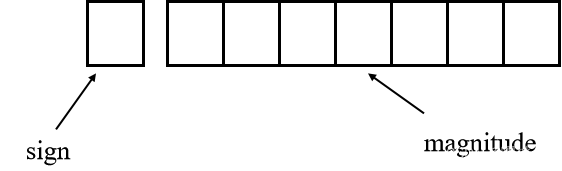
00110100 -> (+110100)_2 = (+52)_10 10010011 -> (-10011)_2 = (-19)_10- 1
- 2
- 最大的值: 01111111 = + 12 7 10 0111 1111 = +127_{10} 01111111=+12710
- 最小的值: 11111111 = − 12 7 10 1111 1111 = -127_{10} 11111111=−12710
- 零: 00000000 = + 0 10 0000 0000 = +0_{10} 00000000=+010 或 10000000 = − 0 10 1000 0000 = -0_{10} 10000000=−010
因此,8比特组成的数字的范围: − 12 7 10 t o + 12 7 10 -127_{10} to +127_{10} −12710to+12710
对于 n 位sign-and-magnitude表示,可以表示的值的范围是多少? − ( 2 n − 1 − 1 ) 10 到 + ( 2 n − 1 ) 10 -(2^{n-1}-1)_{10} 到 +(2^{n-1})_{10} −(2n−1−1)10到+(2n−1)10
如果要把一个数字进行正负转换,只需要转换符号位。
例如:0010 0001 (33) -> 1010 0001 (-33) 1000 0101 (-5) -> 0000 0101 (5)- 1
- 2
(2)第一类补数方式
1s Complement给定一个可以表示为 n 位二进制数的数字 x,它的否定值可以使用 1s 补码表示获得:
− x = 2 n − x − 1 -x = 2^n - x - 1 −x=2n−x−1例如,将8比特数 0000 1100(12)转换为-12:
− 00001100 = 2 8 − 12 − 1 = 243 = 11110011 ( 1 ′ s ) −00001100=28−12−1=243=11110011(1′s) −00001100=28−12−1=243=11110011(1′s)使用第一类补数方式,对数值取反的方法:反转所有比特
- 最大值: 0111 1111 = +127
- 最小值:1000 0000 = -127
- 零: 0000 0000 = +0 或 1111 1111 = -0
- 8比特可表示的范围: -127 to +127
- n比特可表示的范围: − ( 2 n − 1 − 1 ) 到 2 n − 1 − 1 -(2^{n-1} - 1) 到 2^{n-1} -1 −(2n−1−1)到2n−1−1
最高位比特
most significant bit(MSB)仍然表示符号(0为正,1为负)例子
(14)_10 = (0000 1110)_2 = (0000 1110)_1s -(14)_10 = -(0000 1110)_2 = (1111 0001)_1s -(80)_10 = -(0101 0000)_2 = (1010 1111)_1s- 1
- 2
- 3
(3)第二类补数方式
2s Complement给定一个可以表示为 n 位二进制数的数字 x,它的取反值可以使用 2s 补码表示获得:
− x = 2 n − x -x = 2^n - x −x=2n−x例如,8-bit数 0000 1100(12)在第二类补数方式里是这样表示的:
− 00001100 = 2 8 − 12 = 244 = 11110100 ( 2 ′ s ) −00001100=28−12=244=11110100(2′s) −00001100=28−12=244=11110100(2′s)使用第一类补数方式,对数值取反的方法:反转所有比特后+1
- 最大值: 0111 1111 = +127
- 最小值: 1000 0000 = -128
- 零: 0000 0000 = +0
- 8比特可表示的范围:-128 到 +127
- n比特可表示的范围:
−
2
n
−
1
到
2
n
−
1
−
1
-2^{n-1} 到 2^{n-1}-1
−2n−1到2n−1−1
最高位比特most significant bit(MSB)仍然表示符号(0为正,1为负)
例子
+(14)_10 = (0000 1110)_2 = (0000 1110)_2s -(14)_10 = -(0000 1110)_2 = (1111 0010)_2s -(80)_10 = -(0101 0000)_2 = (1011 0000)_2s- 1
- 2
- 3
(4)比较
Comparisons
(5)小数的补数
Complement on Fractions我们可以在小数上扩展补码的概念。
0101.01 -> 1010.10 (1s) 111000.101 -> 000111.010 (1s) 0101.01 -> 1010.11 (2s)- 1
- 2
- 3
(6) 第二类补数方式的加减法
2s Complement Addition/Subtraction加法 A+B
- 每一位二进制数相加
- 忽略符号位的进位
- 检查溢出。 如果 符号位的“carry in(进位)”和“carry out”不同,或者结果与 A 和 B 的符号相反,则会发生溢出。
减法 A-B = A + (-B)
- 计算B的2s补数
- 将其和A相加
溢出问题
有符号数的范围是固定的。
如果加/减的结果超出这个范围,就会发生溢出。可以很容易地检测到溢出:正数加正数变成负数,负数加负数变成正数。
例如:在4-bit 2s-complement系统下,
- 可表示数值范围: -8 to +7
0101 + 0110 = 1011 -> 5 + 6 = -5 ⇒ 溢出了 1001 + 1101 = 10110 (忽略首位进位) = 0110 -> -7 + -3 = 6 ⇒ 溢出了- 1
- 2

(7) 第一类补数方式的加减法
1s Complement Addition/Subtraction加法 A+B
- 对两个数进行二进制加法。
- 如果 MSB 有进位,则结果加 1。
- 检查溢出。 如果结果与 A 和 B 的符号相反,说明发生溢出。
减法 A-B = A + (-B)
- 计算B的1s补数
- 将其和A相加

(8)超额表示
Excess Representation除了sign-and-magnitude和补码方案,超额表示是另一种方案。
它允许值的范围通过简单的转换(加法/减法)在正值和负值之间均匀分布。
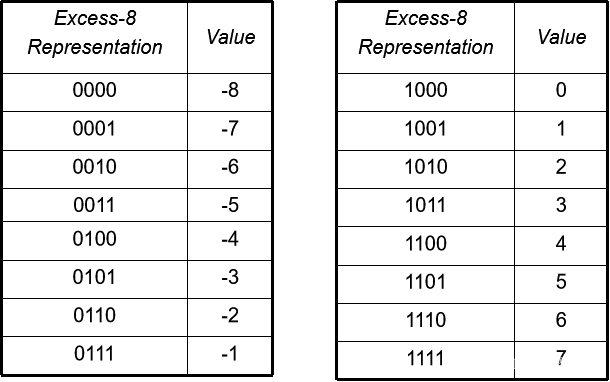
示例: 3 位数字上的 Excess-4 表示。 见表。
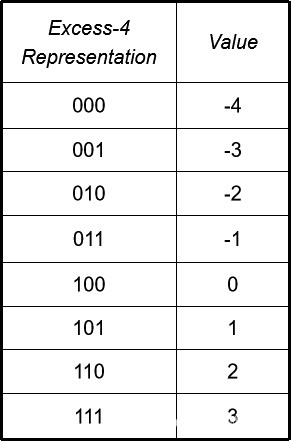
对于 4 位数字,我们可以使用excess-7 或excess-8。 Excess-8 如下所示。
1.11 实数表示方式
很多应用不仅包含整数计算,还包含实数的计算。
那么在计算机系统里如何表示实数呢?
因为比特的数量有限,实数通常会表示为一个大致的值。(1) 定点表示
Fixed-point Representation在定点表示方式中,给整数/小数部分的比特位数量是固定的。
例如,给定一个8-bit的表示,其中6bit是整数部分,2bit是小数部分。
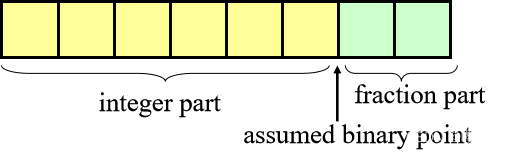
如果我们使用2s complement,我们可以表示数字如下:
011010.11(2s) = 26.75(10)
111110.11 (2s) = -000001.01(2) = -1.25(10)(2)浮点表示
Floating-Point Representation定点表示方式有一个有限的范围。而浮点表示方式允许我们表示非常大/非常小的数字。例如:0.23 * 10^23
浮点表示方式中有3个组成部分:符号
sign、指数exponent、小数mantissa(fraction)

基数为2。
包括两种形式:- 单精度
Single-precision, 32bits:1-bit 符号位,8-bit 带127偏差的指数位(excess-127),23-bit的小数位。 - 双精度
Double-precision, 64bits:1-bit符号位,11-bit 带1023偏差的指数位(excess-1023),52-bit的小数位。
小数会被规范化为整数部分只有一个1,
例如:
110.1 -> normalised -> 1.101 * 2^2 -> 只有后面的101会被存在小数区域。
0.00101101 -> normalised -> 1.01101 * 2^-3 -> 只有后面的01101会被存在小数区域。例子
-6.5在IEEE 754 单精度浮点格式中是如何表示的?
-6.5 = -110.1 = -1.101 * 2^2- Exponent = 2 + 127 = 129 = 10000001
- mantissa = 101
- sign = 1
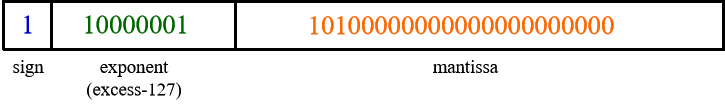
将其写为16进制表示:
1 10000001 10100000000000000000000 = C0D00000
作为不同的数据类型,表示的数也不一样:

2. MIPS I 基础
维基百科定义:
MIPS(Microprocessor without Interlocked Pipeline Stages),是一种采取精简指令集(RISC)的指令集架构(ISA)。2.1 指令集架构
Instruction Set Architecture, ISA2.1.1 定义
- ISA是硬件和低等级软件之间的抽象接口。
- 软件:需要被翻译成指令集
- 硬件:实现指令集的操作
2.1.2 概念
- ISA
- 对于程序员:包含了所有怎么让机器指令正确工作的内容。
- 对于计算机 系统设计人员:可以把精力放在关注程序的功能上,而非硬件如何实现上。
- 这种抽象让不同成本和性能的硬件能运行相同的软件
- 例子:Intel x86/IA-32 ISA指令集架构已经应用在不同的处理器上(从1985年的80386到2005年的Pentium 4)。
- 其他的公司,如AMD和Transmeta也应用了IA-32 ISA。
- 用IA-32 ISA编译的程序可以运行在任意的这些硬件上。
2.2 机器指令和编译语言区别
- 机器指令
- 指令为二进制形式
如:1000110010100000是一条让计算机将两个数字相加的指令。 - 对于程序员来说是非常困难且繁琐的。
- 指令为二进制形式
- 编译语言
- 机器指令的符号化表示,可读性高。
如:add A, B等同于1000110010100000 - 编译器的功能:把编译语言翻译成机器指令
- 编译语言能提供“伪指令”(作为一种语法糖
syntactic sugar) - 在分析性能的时候,需要考虑的是(硬件层面)真实发生的指令
- 机器指令的符号化表示,可读性高。
2.3 处理流程
Walkthrough示例(C语言 -> 编译语言)
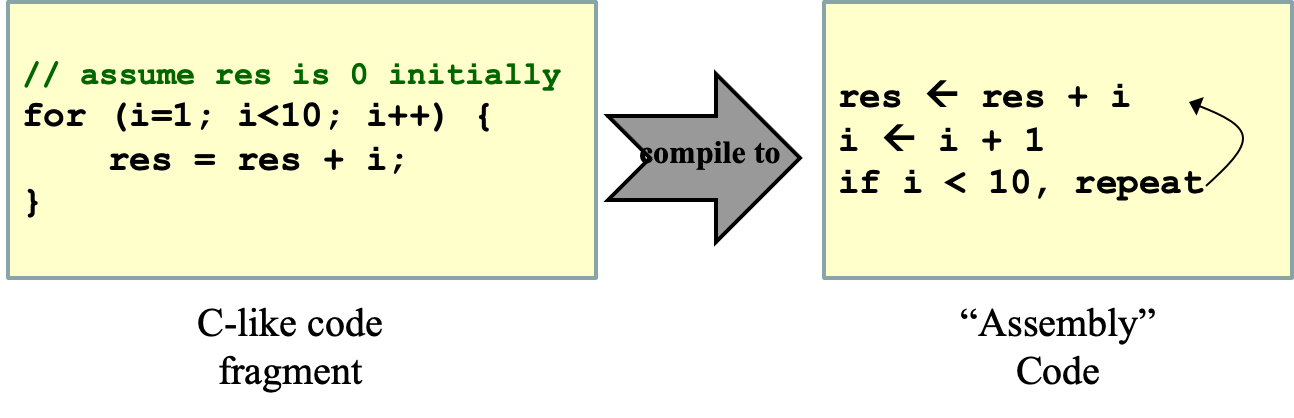
重要组件
在计算机里的两大重要组成部分:处理器和内存
Processor and Memory
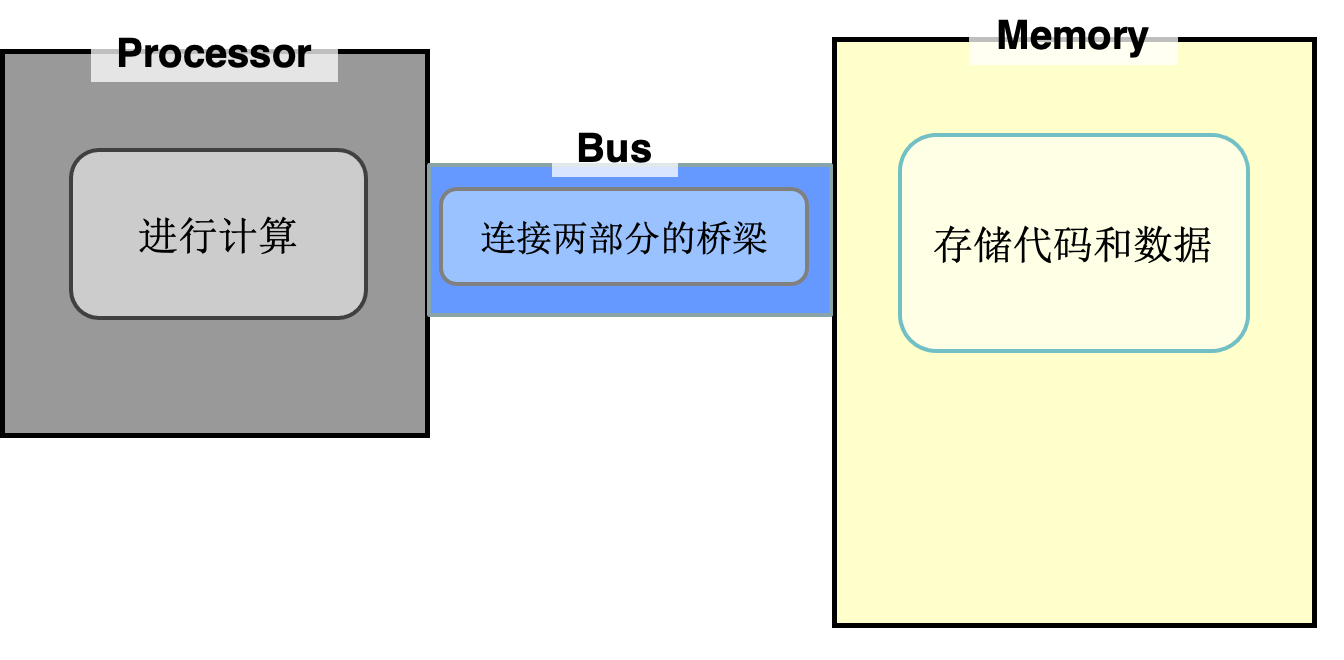
指令操作
代码和数据保存在内存当中,在运行时装入处理器。
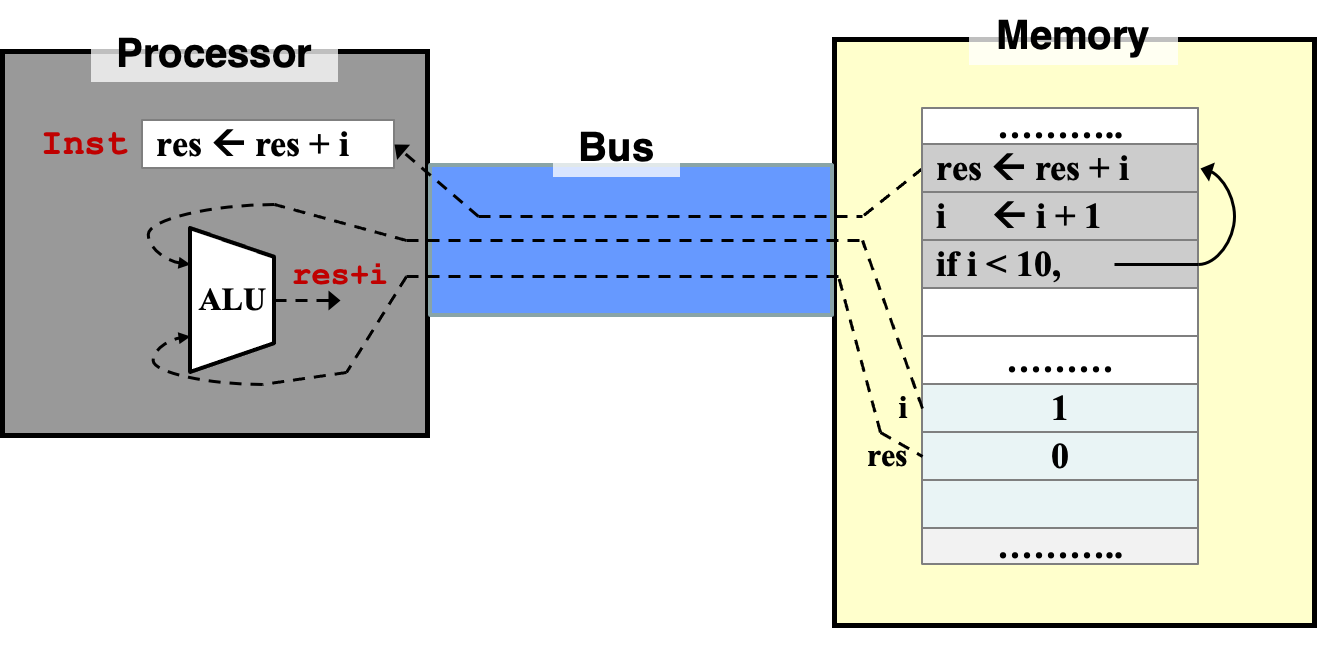
访问内存
访问内存是很慢的,为了避免频繁地访问内存,在处理器中提供了一种用于暂时存储数据的结构,叫做寄存器
register
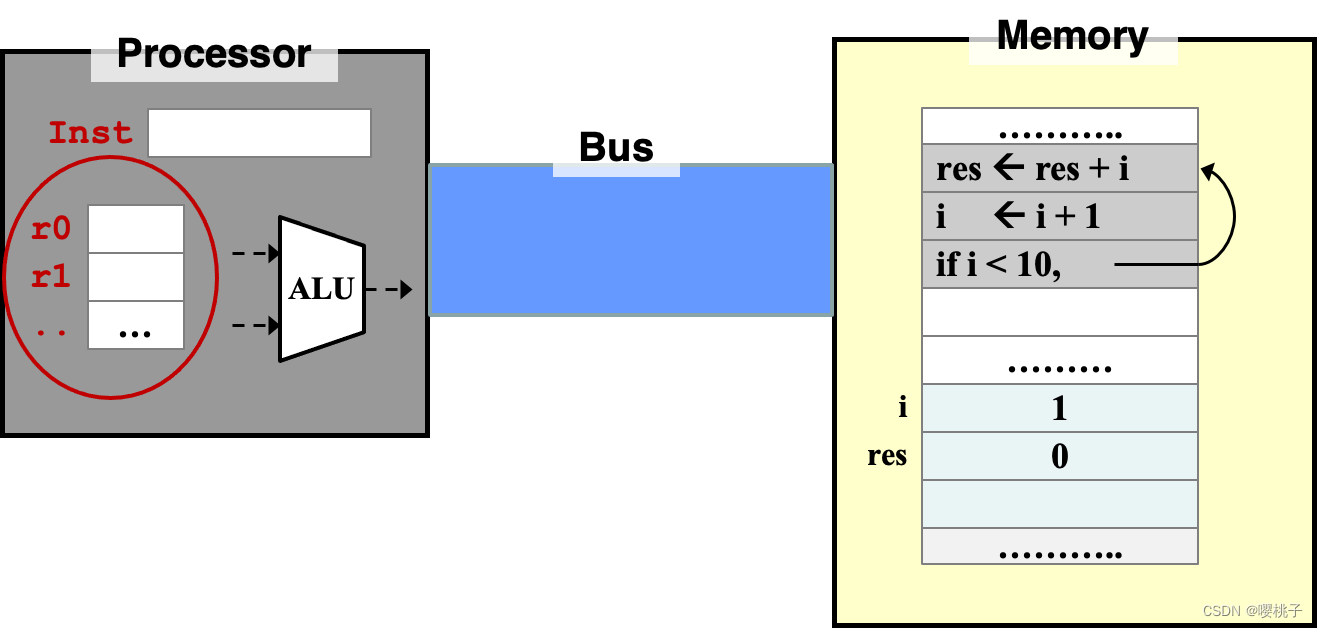
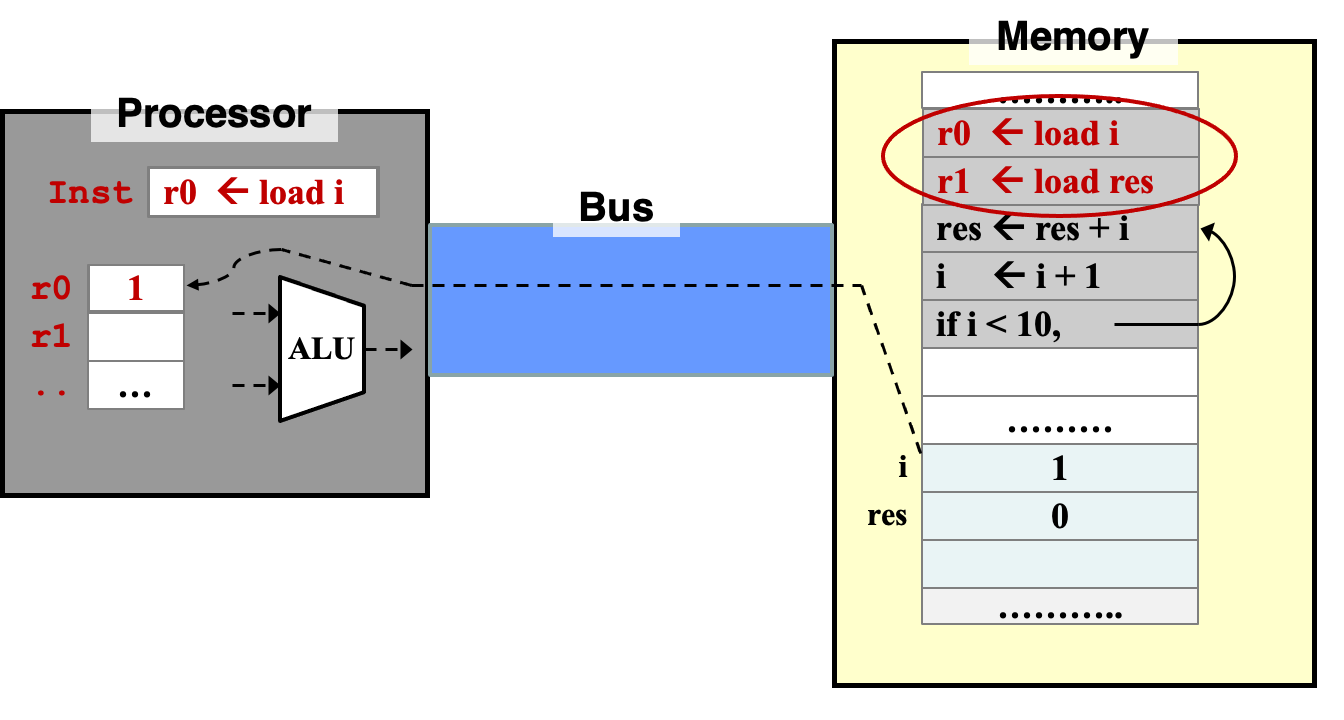
- 我们需要用指令将数据从内存移入寄存器 / 从寄存器移出到内存。
- 从内存移入寄存器:
load - 从寄存器移出到内存:
store
- 从内存移入寄存器:
- 算数运算
Reg2Reg Arithmetic operation可以直接在寄存器上操作,这样速度可以更快。
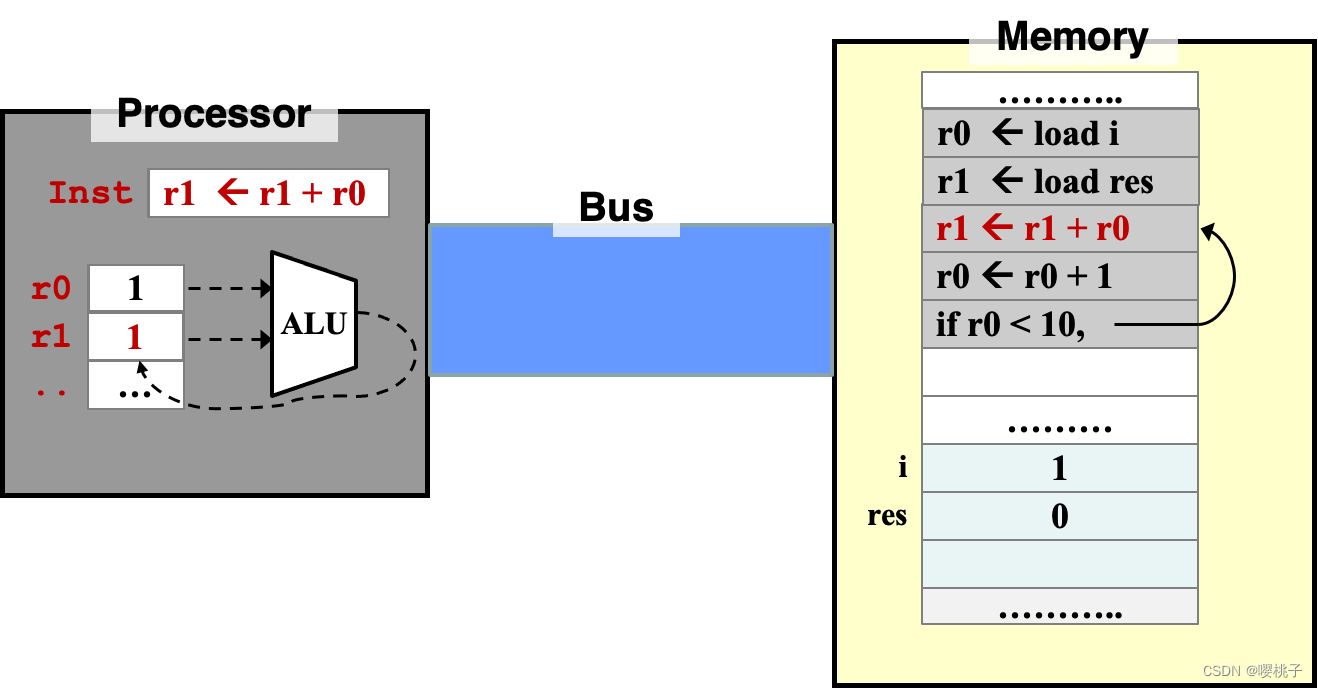
- 算数运算可以用一个常量值(而不是寄存器中的变量)来进行运算
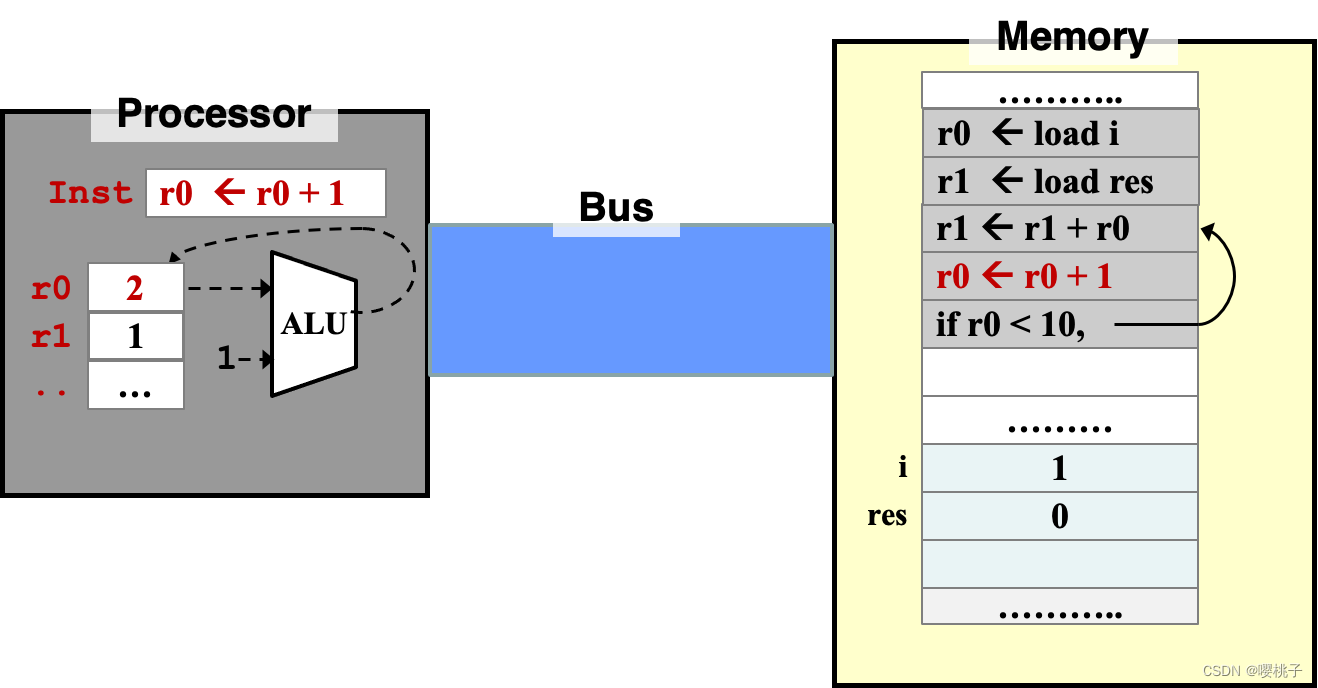
指令执行顺序
- 默认情况下,指令按顺序执行。
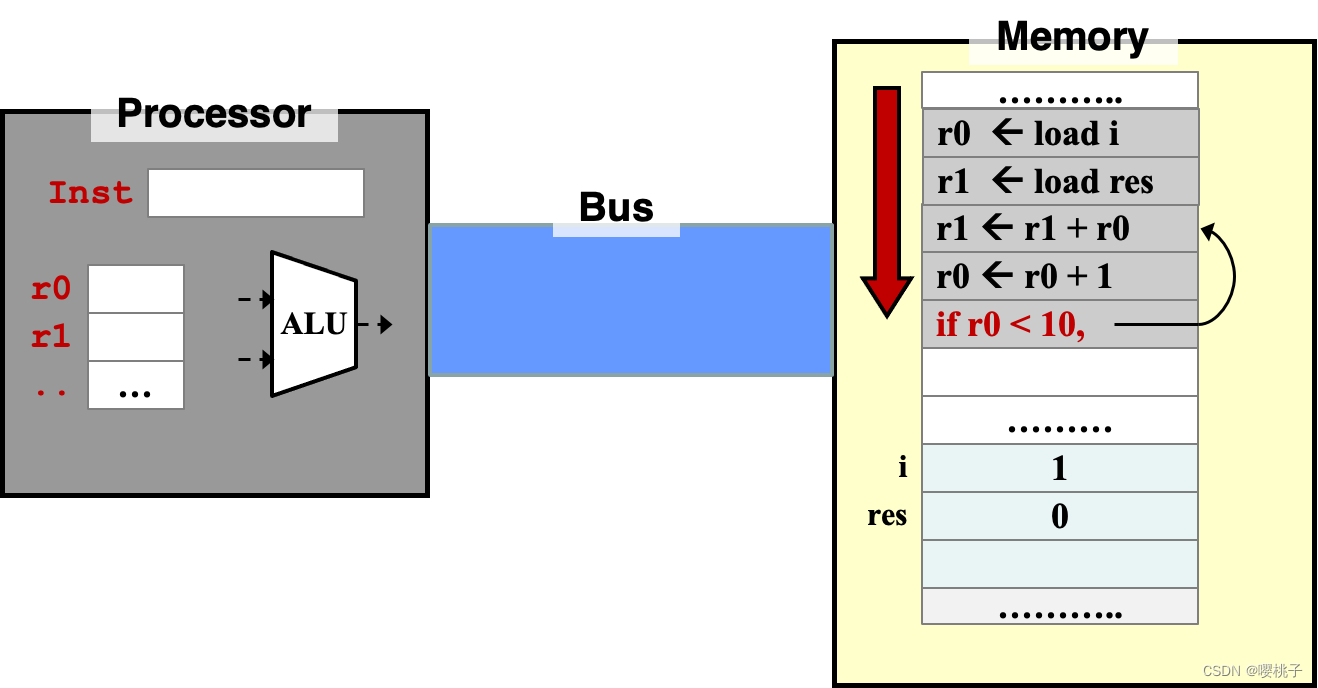
- 循环
repetition (loop)、选择Selection(if-else)需要用指令来切换控制流control flow- 循环:
- 当条件满足时,程序会从声明的位置处开始重复执行;
- 直到遇到下一个控制流指令,程序是继续按顺序往下执行的;
- 直到无法满足条件判断指令
condition fails,跳出该段程序。
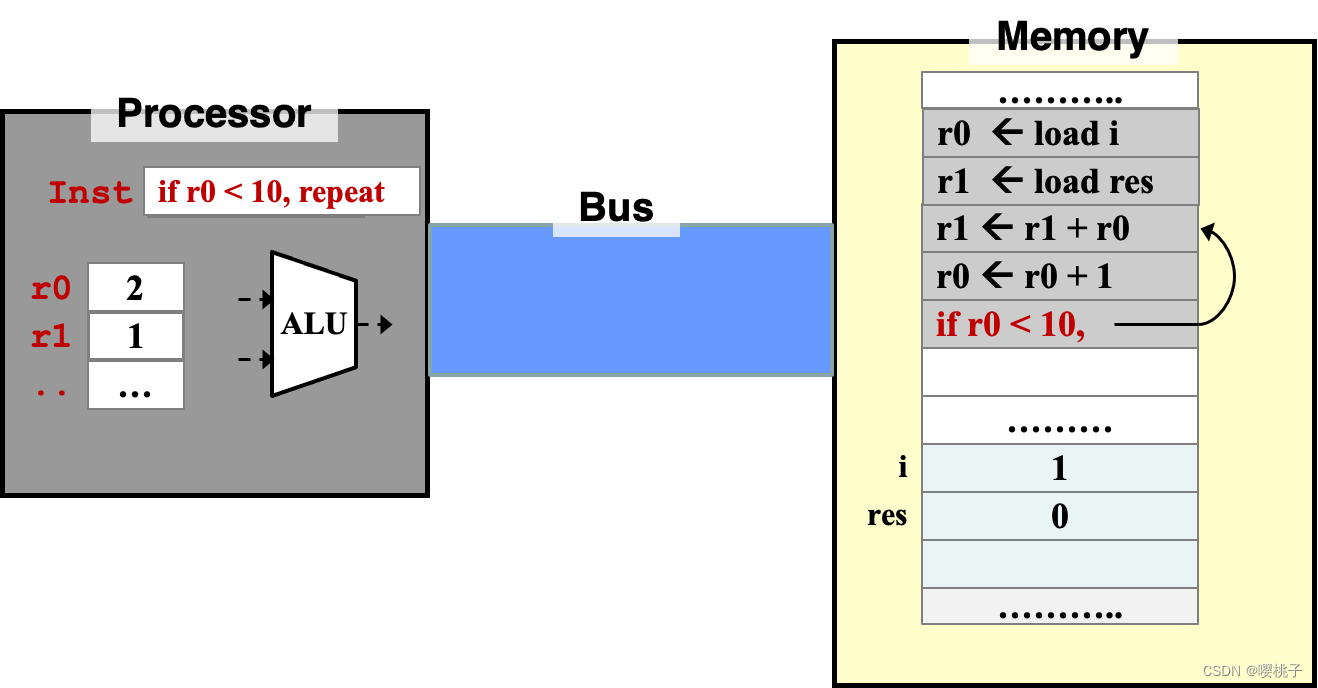
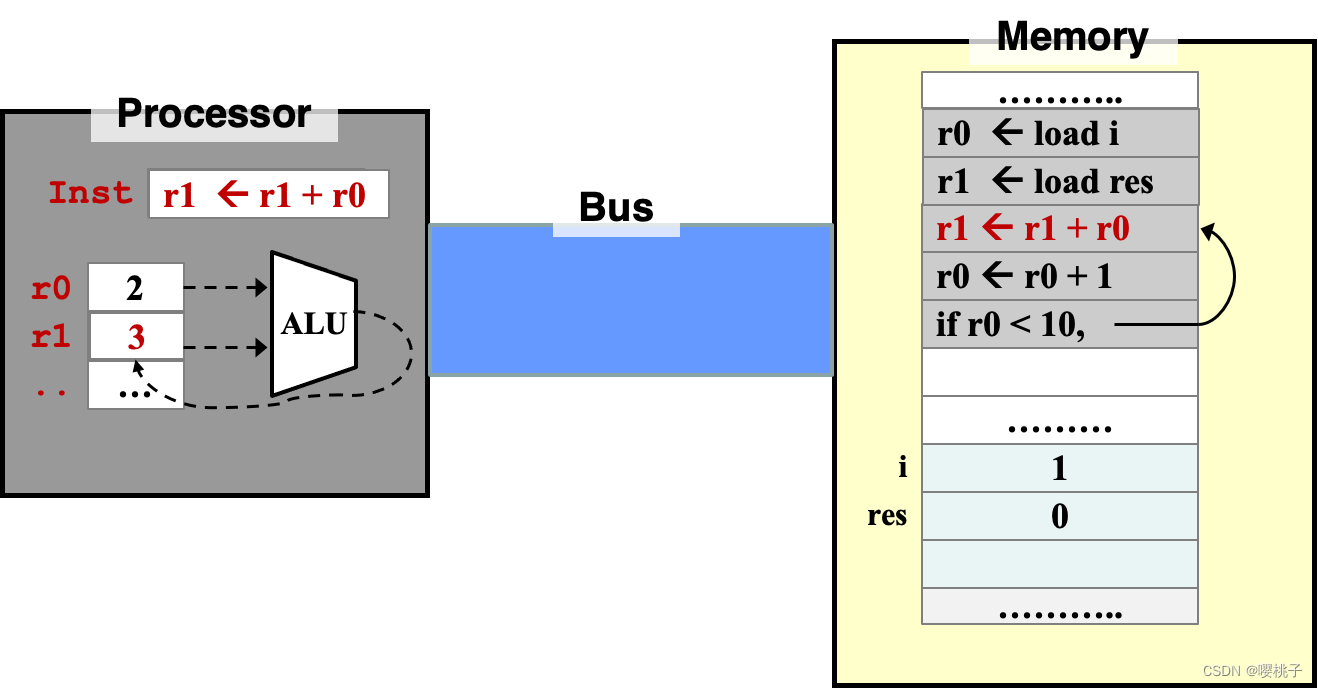
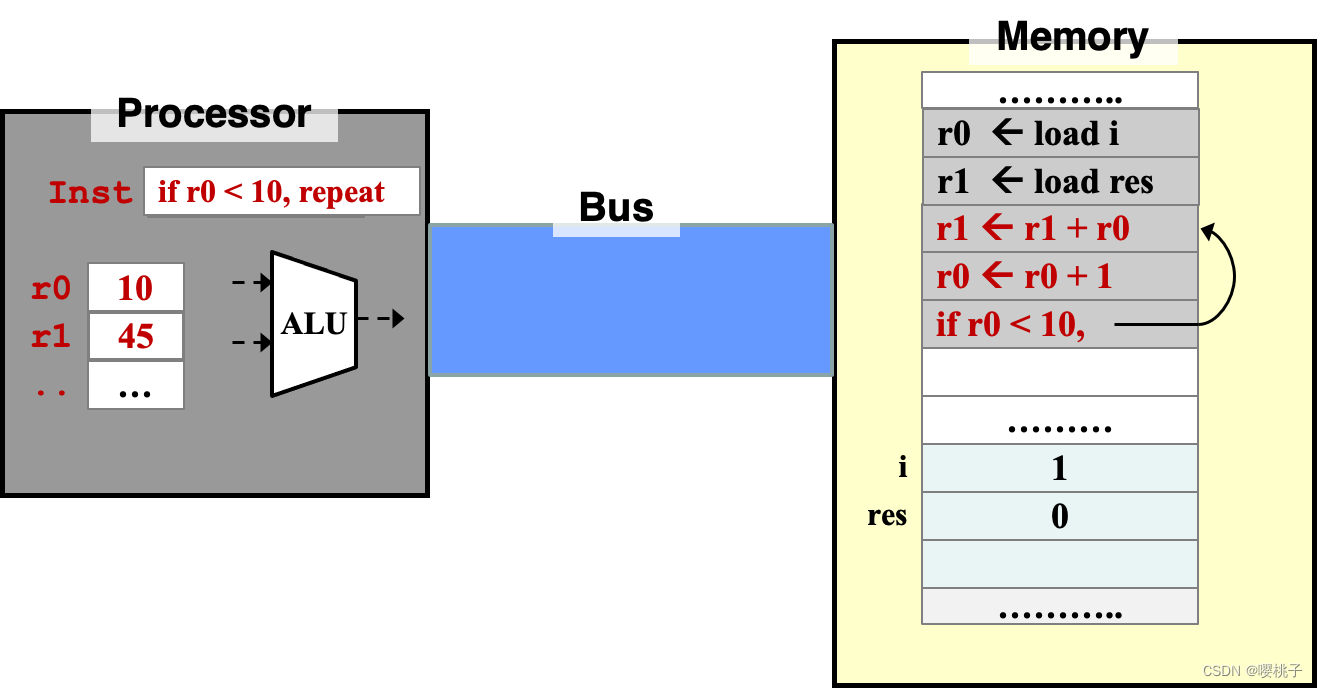
- 循环:
内存指令
Memory Instruction计算过程完成后,可以将寄存器的内容放回内存。
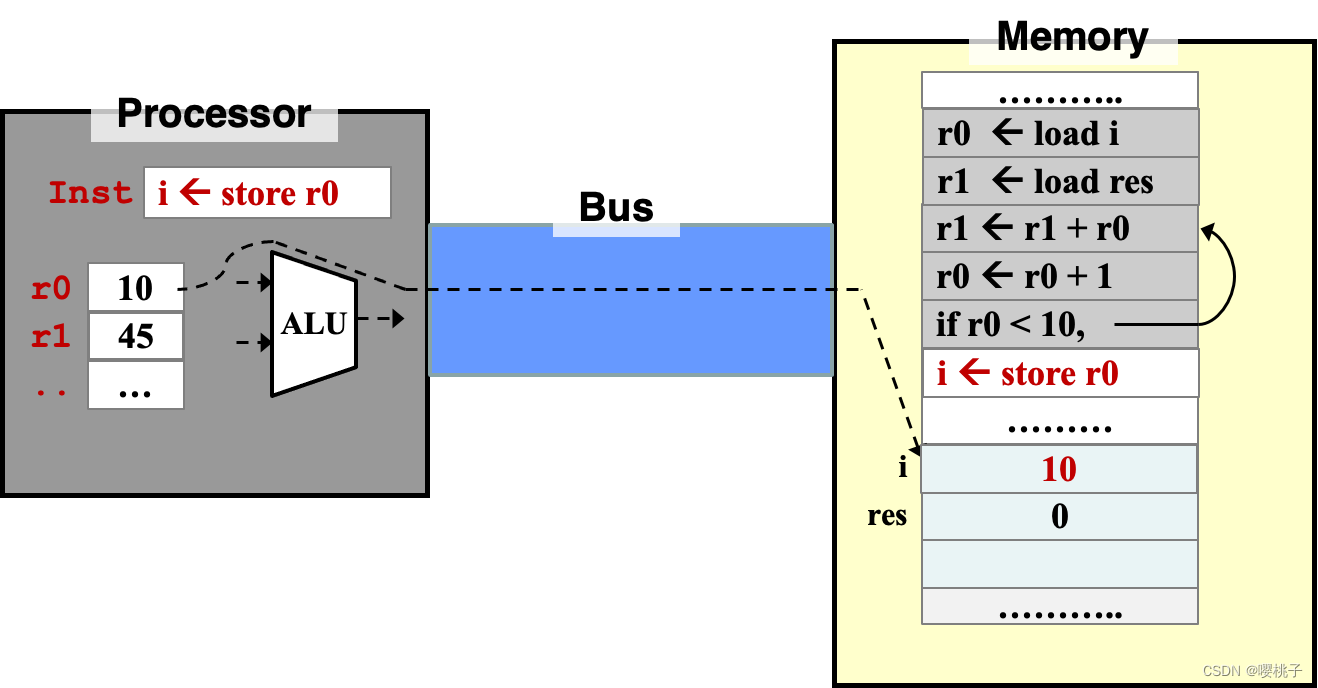
总结
Summary- 存储于内存的概念
stored-memory concept:指令和数据都存储在内存当中。 - 读取-存储的模型
load-store model:在执行过程中,减少对内存的操作,更多依赖于寄存器来暂时存储数据。 - 编译指令的主要类型:
- 内存指令
Memory:将数据在内存和寄存器之间转移 - 计算指令
Calculation:算术运算等 - 控制流指令
Control flow:改变执行的顺序
- 内存指令
2.4 寄存器
Registers- 位于在处理器中更快的“内存”:为了更快地处理数据,数据会从内存传输到寄存器里
- 有限的数量
- 一般来说处理器中有
16-32个寄存器 - 编译器负责将程序变量和寄存器变量相关联
- 一般来说处理器中有
- 寄存器
没有数据类型,不像程序变量一样,机器指令/编译指令假设存储在寄存器的数据是类型正确的。
在MIPS编译语言中,有32个寄存器。
- 可以是被数字引用
($0, $1, ..., $31) - 也可以被名称引用
($a0, $t1)
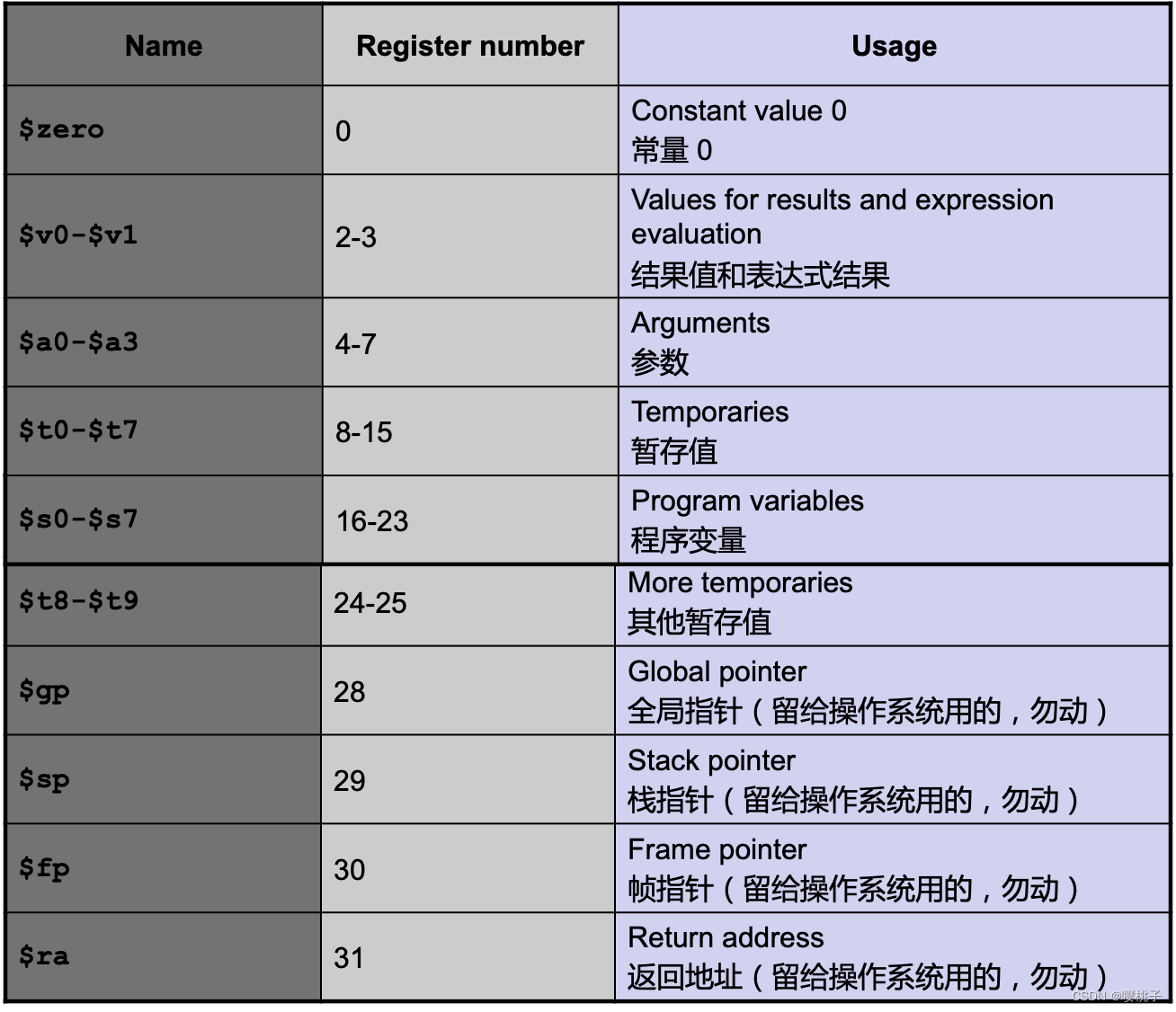
另外, $at (register 1)是留给编译器用的。$k0 - $k1 (register 26-27)是留给操作系统用的。
2.5 MIPS编译语言
- 每个指令用一个简单命令来执行。(通常在高级语言 C/C++/Java…中有对应)
- 每一行编译代码只包含一个指令。
- 注解符号:
#,任何在每一行#后面的都会被编译器忽略
2.5.1 基础语法结构
多数MIPS的算术/逻辑运算都有三个操作数:
2个来源位置和1个目标位置。

2.5.2 算术运算:加法

我们假设a、b、c的数值已经分别装入了寄存器$s0、$s1、$s2(变量映射variable mapping)。(这里没展示内存操作指令。)- ⚠️ 重要概念:MIPS的算术运算主要是 寄存器到寄存器的
register-to-register。
2.5.3 算术运算:减法

$s1 / $s2的位置是很重要的,前减后。2.5.4 复合表达式
Complex Expression
单个MIPS指令最多只能有两个源操作数,因此,需要将复合表达式拆分为多个MIPS指令。

中间数可以用暂存寄存器Temporary registers($t0, $t1)来存储。示例:
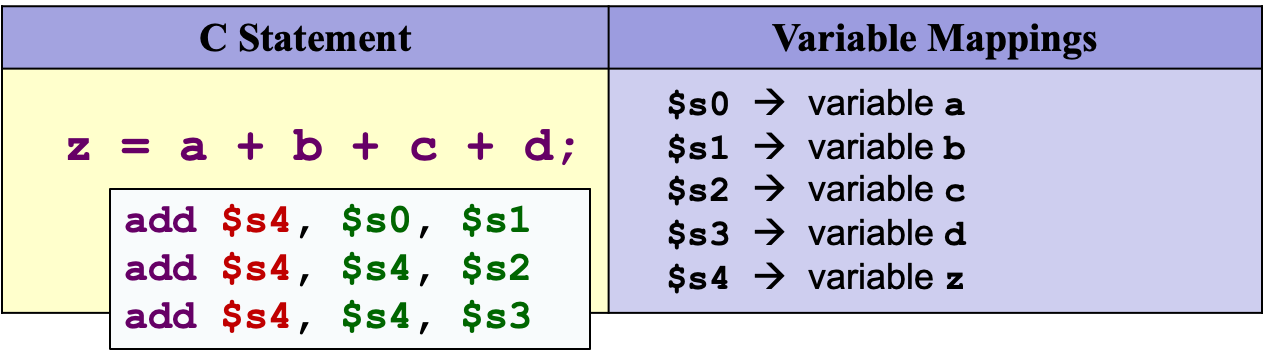
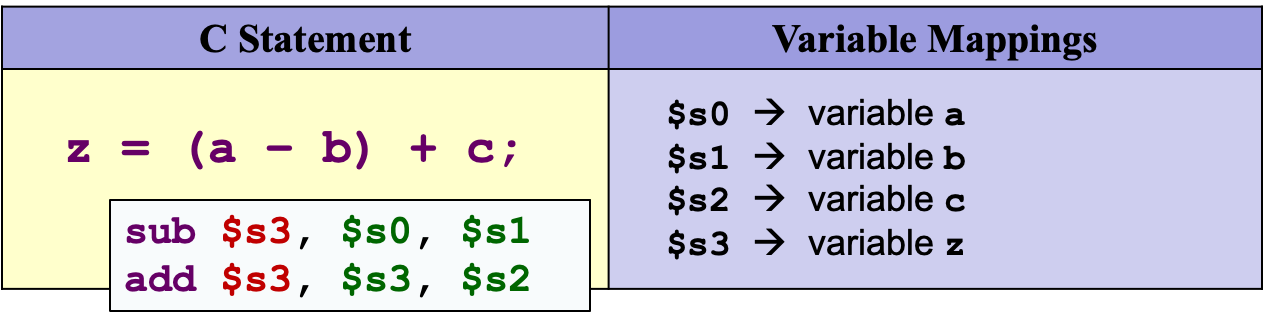
2.5.5 常数操作数
Constant / Immediate Operands
Immediate value是数值常量,经常用于各类操作。MIPS专门为他们提供了一系列操作operations。addi指令:Add Immediate- 语法和
add指令差不多,但是第二个源操作数是一个常量(而不是寄存器变量) - 常量的范围是
[
−
2
15
,
2
15
−
1
]
[-2^{15}, 2^{15}-1]
[−215,215−1] (使用16-bit 第二类补数系统
16-bit 2s complement number system) - 没有
subi指令,因为可以直接用addi加上一个负数。Why?因为芯片是很贵的,有资源限制,指令越少越好。
- 语法和
2.5.6 寄存器零 (
$0 or $zero)- 数字 0 经常在代码中出现,因此提供了一个包含数值0的寄存器零 (
$0 or $zero) 。
例如图示用于赋值操作。

由于这种赋值操作非常常见,MIPS定义了一种伪指令
move。
⚠️注意:这只是为了表示起来比较方便,最后还是要转成上面那种指令的。

2.5.7 逻辑运算
Overview
算术运算将寄存器的内容(32个比特)看作一个整体的量(有符号/无符号的整数);
逻辑运算将寄存器的内容看作分散的32个比特,这样就可以在一个字word里对每个bits/bytes做一些位运算
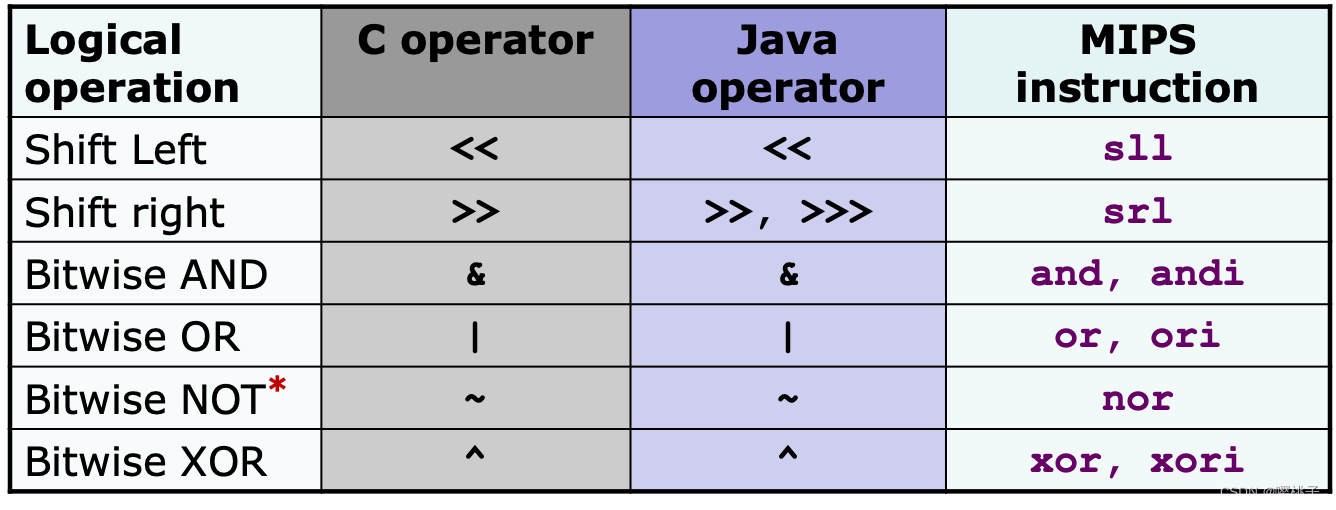
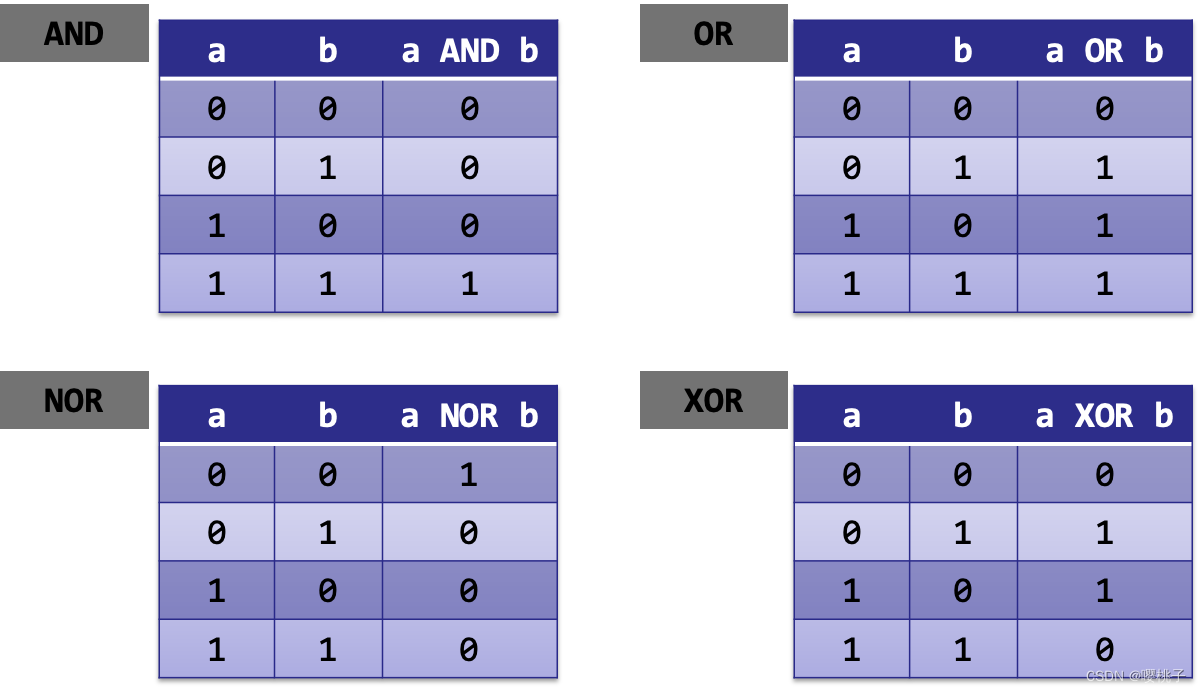
*实际上not指令是不存在的,有些特殊的技巧可以达到取反的效果,后面说。- 0代表false,1代表true。
AND:全是1才是1OR:有1就是1NOR:全是0才是1XOR:exclusive or,异或,不一样才是1
2.5.7.1 移位运算
Shiftingsll (shift left logical):将一个字word中的所有比特向左移动n位,后面补0。
例如,将
$s0左移4位。

srl (shift right logical):将一个字word中的所有比特向右移动n位,前面补0。- 对于比特的左/右移动n位,相当于在数学计算中乘以/除以 2 n 2^n 2n
- 位运算比乘除法快很多
一个好的编译器会将乘除法转换成位运算指令。

2.5.7.1 按位x运算
按位与运算
Bitwise ANDand:按位与运算Bitwise AND,对应位置上都是1,结果才是1,否则为0。
例子:and $t0, $t1, $t2

and可以用作掩码操作masking operation- 在需要忽略的位置,掩码对应位置设为0,则结果对应位置转为0。
- 在需要的位置,掩码对应位置设为1,则结果对应位置与原来保持一致。
例如:我们只对寄存器
$t1的最后12位感兴趣,将结果存在$t0,掩码mask应该是:

按位或运算
Bitwise ORor:按位或运算Bitwise OR,两个字word对应位置其中一个为1结果位置就是1。or指令有一个常数版本ori指令。
这个指令可以用来将部分比特强制转化为1。
例如:ori $t0, $t1, 0xFFF
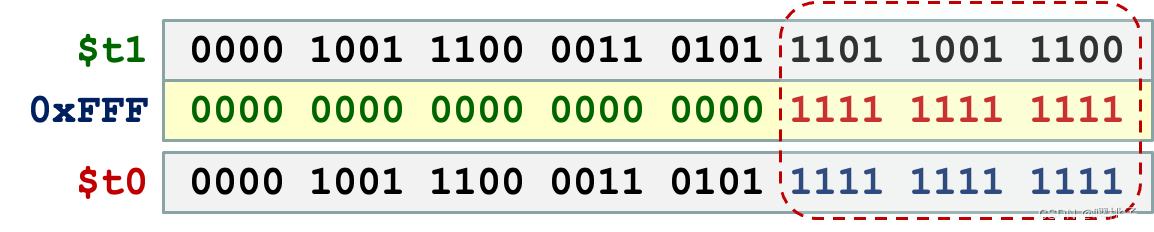
按位或非运算
Bitwise NOR
- 在MIPS中没有
NOT指令(就是0变1,1变0),但提供了一个NOR指令(全是0,结果才是1)。
因此,NOT的效果可以通过nor $t0, $t0, $zero得到。(当某位上是0时,和0 nor,两个都是0,结果为1;当某位上是1时,和0 nor,有一个不是0,结果为0;由此达到0变1,1变0的效果) - 为什么不提供
NOT指令?设计原则:让指令集尽可能小。
按位异或运算
Bitwise XOR
- 如何使用
XOR得到NOT的等效结果?(a XOR 1 -> NOT a)
让$t2的比特位上全为1,执行xor $t0, $t0, $t2。(XOR:不同才是1,当某位上是0时,和1不同,得到1;当某位上是1时,与1相同,得到0) - 为什么在MIPS里,没有
NORI,却有XORI?【待补充】
Case Study:大常数
Large Constant维基百科:CPU 字长的定义就是通用寄存器的宽度,64位CPU是指CPU内部的通用寄存器的宽度为64位元
怎么将一个32位的常数放进寄存器里?如
10101010 10101010 11110000 11110000
Note: 操作常量的范围是 [ − 2 15 , 2 15 − 1 ] [-2^{15}, 2^{15}-1] [−215,215−1] (使用16-bit 第二类补数系统16-bit 2s complement number system)- 用
lui (load upper immediate)指令设置 上16位:lui $t0, 0xAAAA #10101010 10101010
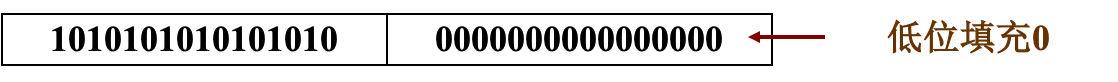
- 用
ori (or immediate)设置低位比特:ori $t0, $t0, 0xF0F0 #11110000 11110000

MIPS基础运算指令总结
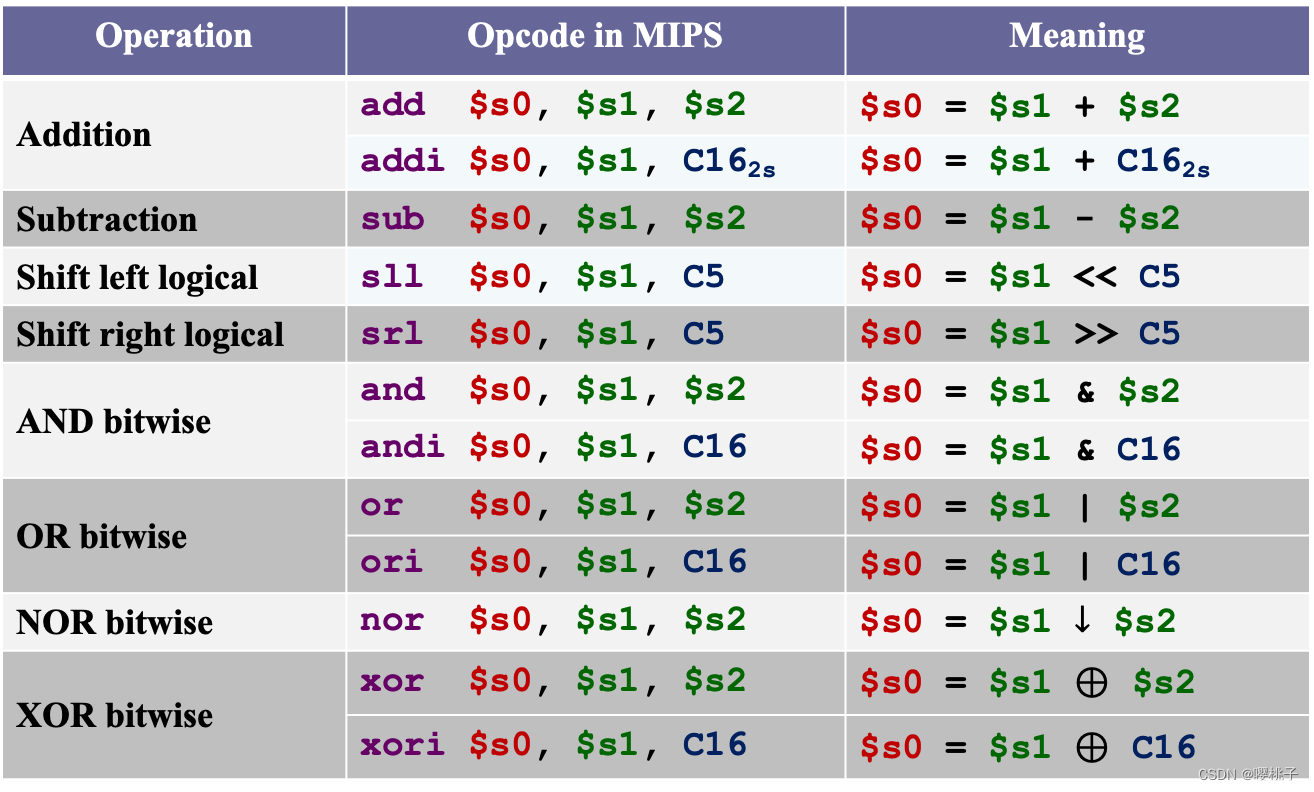
其中,- C5范围是 [ 0 , 2 5 − 1 ] [0, 2^5 - 1] [0,25−1]
- C16范围是 [ − 2 15 , 2 15 − 1 ] [-2^{15}, 2^{15}-1] [−215,215−1],是一个十六位的比特串。
3. MIPS II 进阶
3.1 内存组织
Memory Organisation (General)- 主存储器可以看作是一个巨大的、一维的存储单元数组。
- 每个存储单元都有一个地址
address,就是数组的索引。- 给定一个k比特的地址,说明地址空间有 2 k 2^k 2k
如图,每个存储单元包含了一个字节Byte(8个比特bits)。【字节寻址方式】
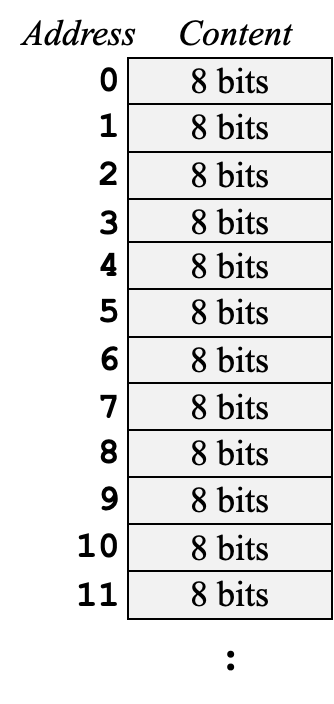
3.1.1 传输单元
Transfer Unit- 根据一个内存地址,我们可以访问到:
- 一个字节(采用字节寻址方式
Byte addressable的机器) - 或一个字(采用字寻址
Word addressable方式的机器)
- 一个字节(采用字节寻址方式
字 WORD:- 通常是 2 n 2^n 2n bytes。(多少位的机器,n就是多少,比如64位机器说的就是他的基本传输单元(字长)是 2 64 2^{64} 264比特)
- word是处理器和内存之间的基本传输单元。
- 通常和该机器上的
寄存器的大小 / 整数的大小 / 指令大小是一样的
维基百科
word: 对于某种特定的计算机设计而言,字(英语:word)是用于表示其自然的数据单位的术语。在这个特定电脑中,字是其用来一次性处理事务的一个固定长度的位(bit)组。一个字的位数(即字长)是电脑系统结构中的一个重要特性。
字长度在计算机结构和操作的多个方面均有体现。电脑中大多数寄存器的大小是一个字长。电脑处理的典型数值也可能是以字长为单位。CPU和内存之间的数据传送单位也通常是一个字长。还有在内存中用于指明一个存储位置的地址也经常是以字长为单位的。3.1.2 字的排列
Word Alignment如果word的起始字节地址 是word中字节数的倍数,则word在内存中对齐。(所以找下一个字就地址+4)
例子:如果一个字包含4个字节:
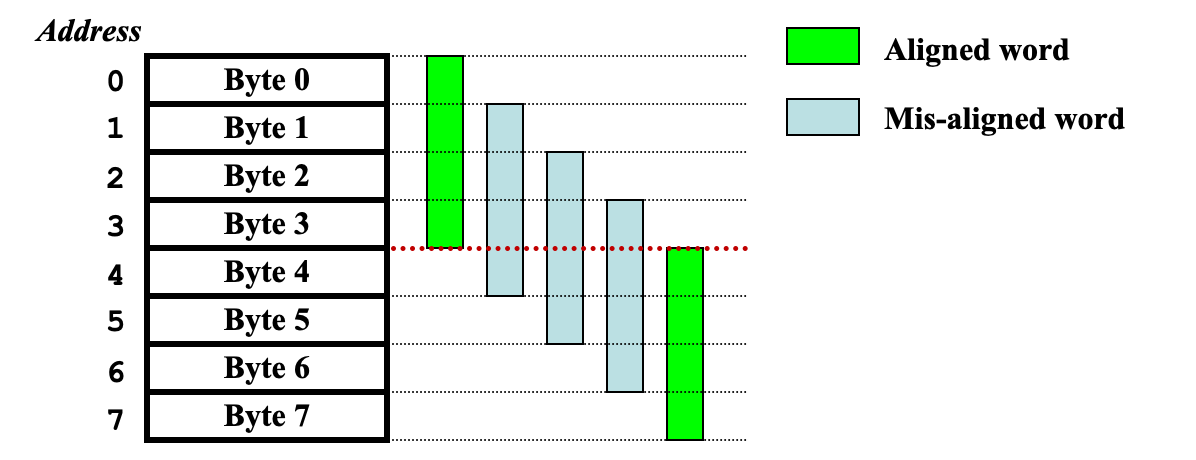
我们怎么快速判断一个给定的内存地址是不是word-aligned的?
看看起始位置能不能被word中字节数整除。3.2 MIPS内存指令
Memory Instructions- MIPS是一种读取-存储
load-store寄存器架构。- 共有32个寄存器,每个长32-bit(4 bytes)
- 每个word包含32 bits (4 bytes)
- 内存地址长32 bits(Why?这样他们就能刚好存进寄存器了)

3.2.1 读取 字word
Load Word例:
lw $t0, 4($s0)步骤:
- 内存地址 =
$s0+ 4 = 8000 + 4 = 8004 - 将内存中起始地址为8004的一个word(4字节,
Mem[8004], 8004-8007)读取到$t0
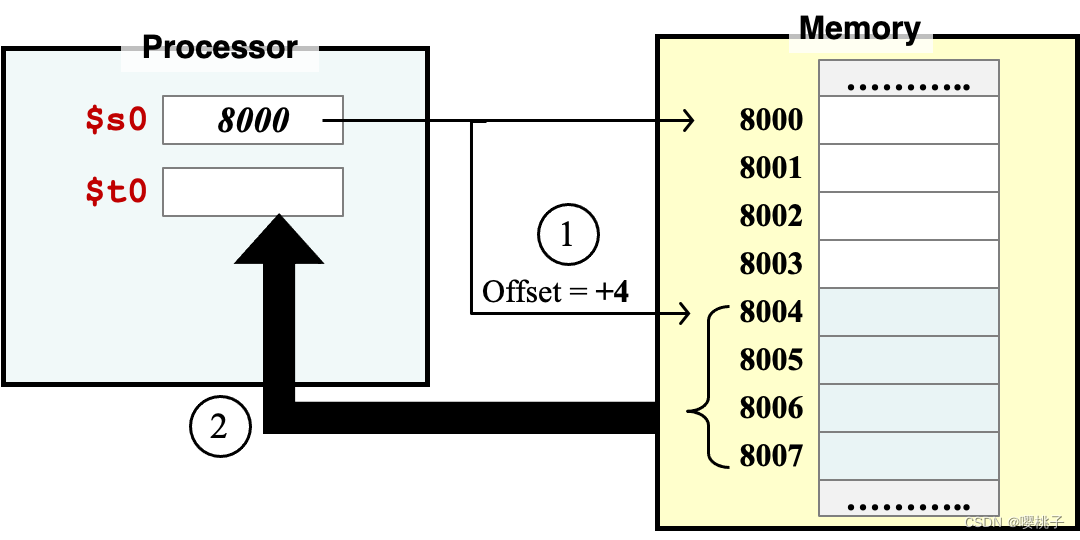
3.2.2 存储 字word
store word例:
sw $t0, 12($s0)步骤:
- 内存地址 =
$s0+ 12 = 8000 + 12 = 8012 - 将
$t0的内容存储到 起始地址为8012的一个word里(Mem[8012], 8012-8015)
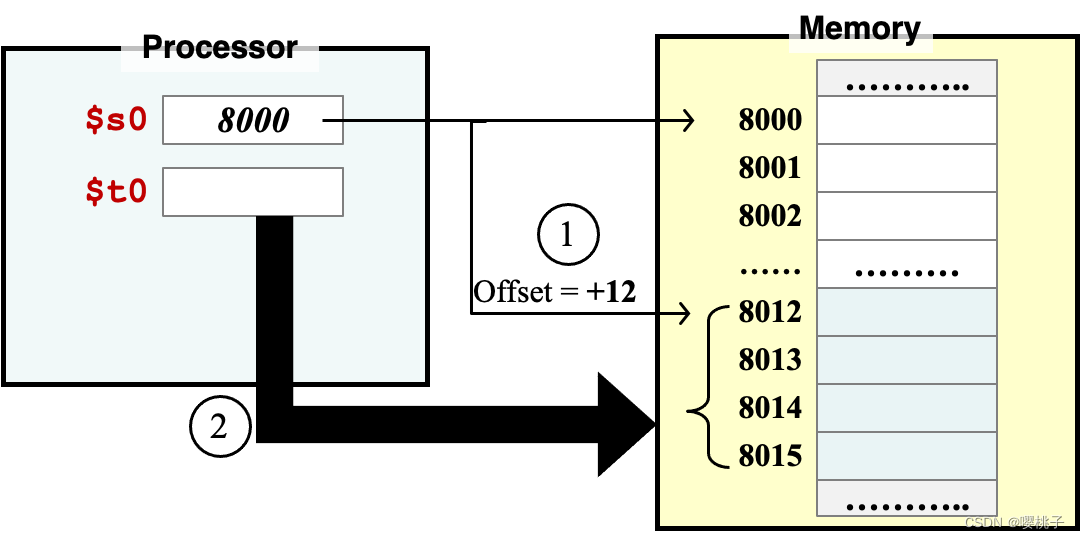
3.2.3 读取和存储指令
load and store instructions只有
load和store指令可以访问内存中的数据。例:每个数组元素占据一个word(4 bytes)。
$s3包含了数组A的起始地址(A[0]的地址)h被映射为$s2
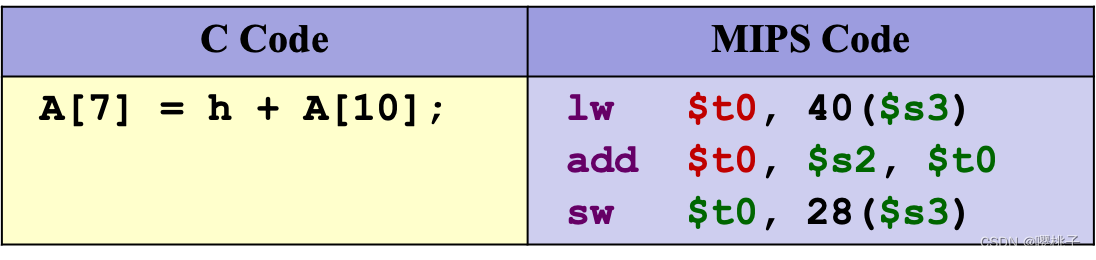
(40 = 4 * 10, 28 = 4 * 7)
3.2.4 其他内存指令
除了
lw和sw外,还有:lb: load byte,读取字节sb: store byte,存储字节
他们的格式都差不多(这里偏移量
offset也不用乘以4了):lb $t1, 12($s3)sb $t2, 13($s3)
注意:
MIPS不允许用lw/sw存取非对齐字unaligned word,如果一定要存取非对齐字,可以使用伪指令ulw/usw (unaligned load word / unaligned store word)。- 其他内存指令
lh / sh:存取半个字load/store halfwordlwl / lwr / swl / swr:存取在左右边的字load/store word left/right
3.2.5 示例:数组
Array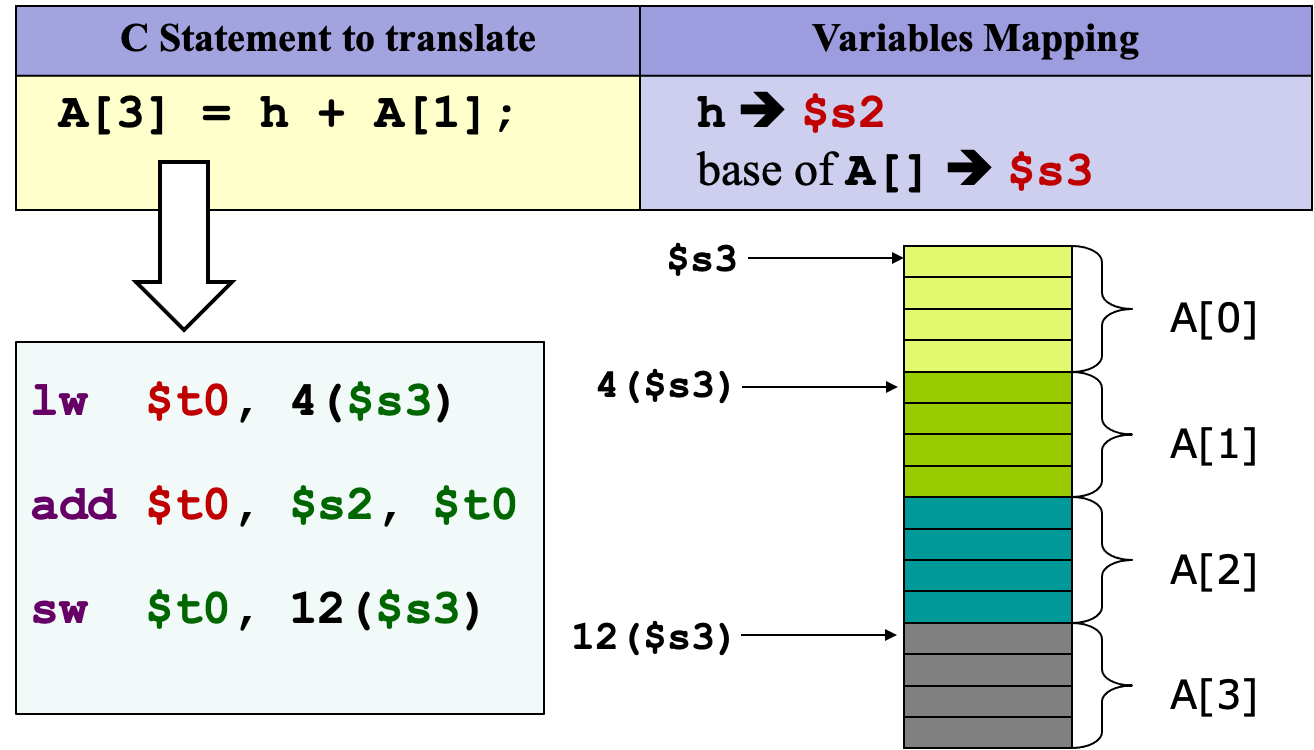
3.2.6 常见问题
地址 vs 数值
⚠️ 注意:寄存器没有数据类型!
- 一个寄存器可以保存任意的32-bit数字
- 这个数字没有明确的数据类型,会根据使用它的指令来解释
例如:
add $t2, $t1, $t0:$t1, $t0应该是数值lw $t2, 0($t0):$t0则应该是地址
字节Byte vs 字Word
⚠️ 注意:在以字节寻址的机器,连续的字地址序列不是相差1的。
通常会犯的错误:认为下一个字的地址可以通过寄存器中存放的地址 + 1得到,实际上应该是寄存器中存放的地址 + 字长对于
lw和sw:基础地址 + 偏移量base address + offset必须是4的倍数。3.2.7 示例:交换元素
Swapping Elements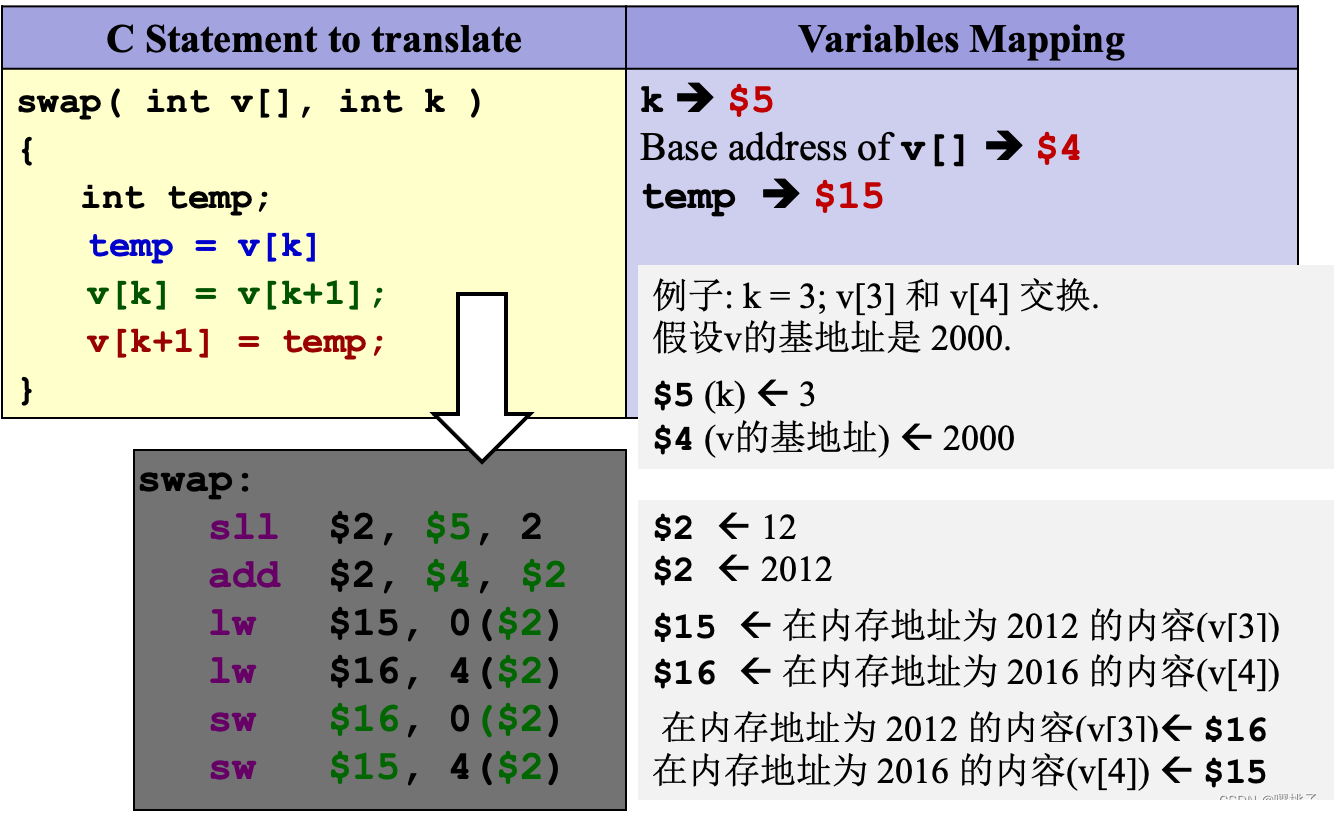
(注:这是个简化版本,不是完整的指令)3.3 做决策
Make decisions- 通常执行一个计算任务,我们需要:做决策、迭代
- 在高级语言中,使用
if / goto语句 - MIPS中的决策指令类似于带goto的if语句。
- goto一般不太好用在高级语言里, 但是却在编译语言中是必须的。
- 在高级语言中,使用
- 决策指令
- 切换程序的控制流
control flow - 改变下一条被执行的指令
- 切换程序的控制流
- MIPS中的两种决策语句
- 条件分支语句
bne $t0, $t1, labelbeq $t0, $t1, label
- 非条件跳转语句 jump
j label
⚠️label是编译语言中的“锚点anchor”,用于标识目标位置,label不是 一种指令。
- 条件分支语句
3.3.1 条件分支语句:相等/不等
Conditional Branch: beq and bne当某个条件满足时,处理器才会进入某一分支。
-
beq $r1, $r2, L1:当r1 r2相等时,跳转到label为L1的指令 (if (a == b) goto L1)
beq: brach if equal -
bne $r1, $r2, L1:当r1 r2不相等时,跳转到label为L1的指令 (if (a != b) goto L1)
bne: brach if not equal
3.3.2 无条件跳转
Jump: j处理器始终会进入该分支。
j L1:无条件进入label为L1的指令 (goto L1)- 等同于 ⇒
beq $s0, $s0, L1
3.3.3 条件判断语句
IF statement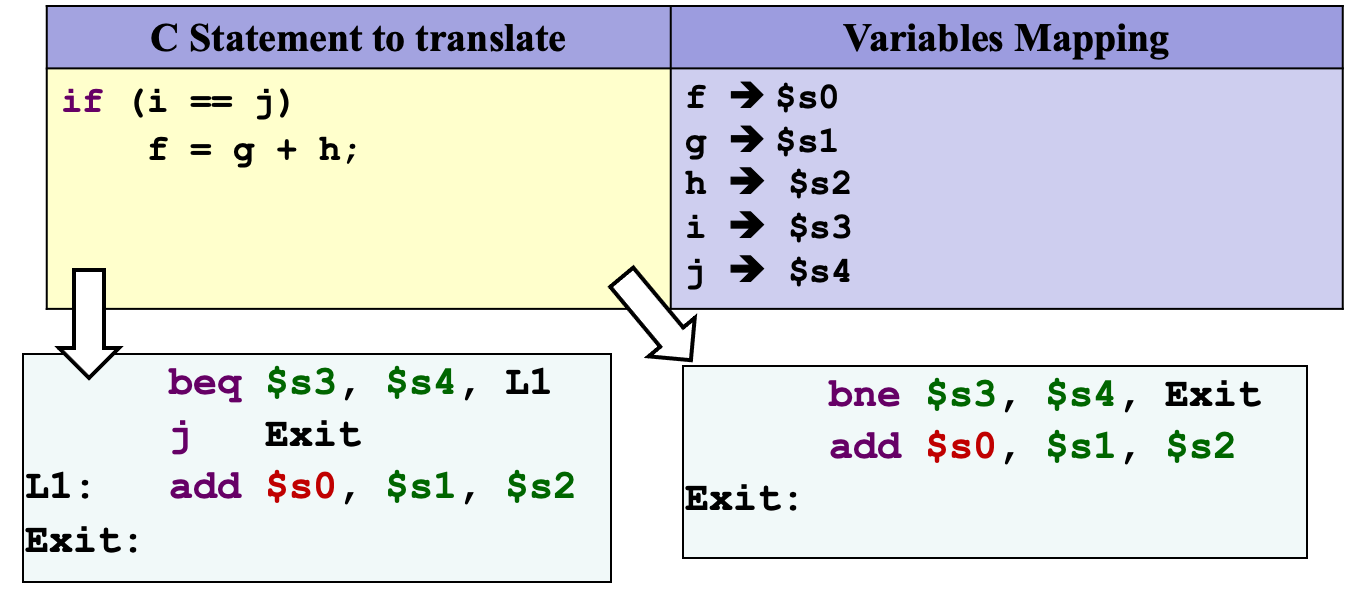
这两种等效的方式,右边效率更高。
⇒ 因此引申出一个通常的技巧:将条件倒过来,用更短的代码执行。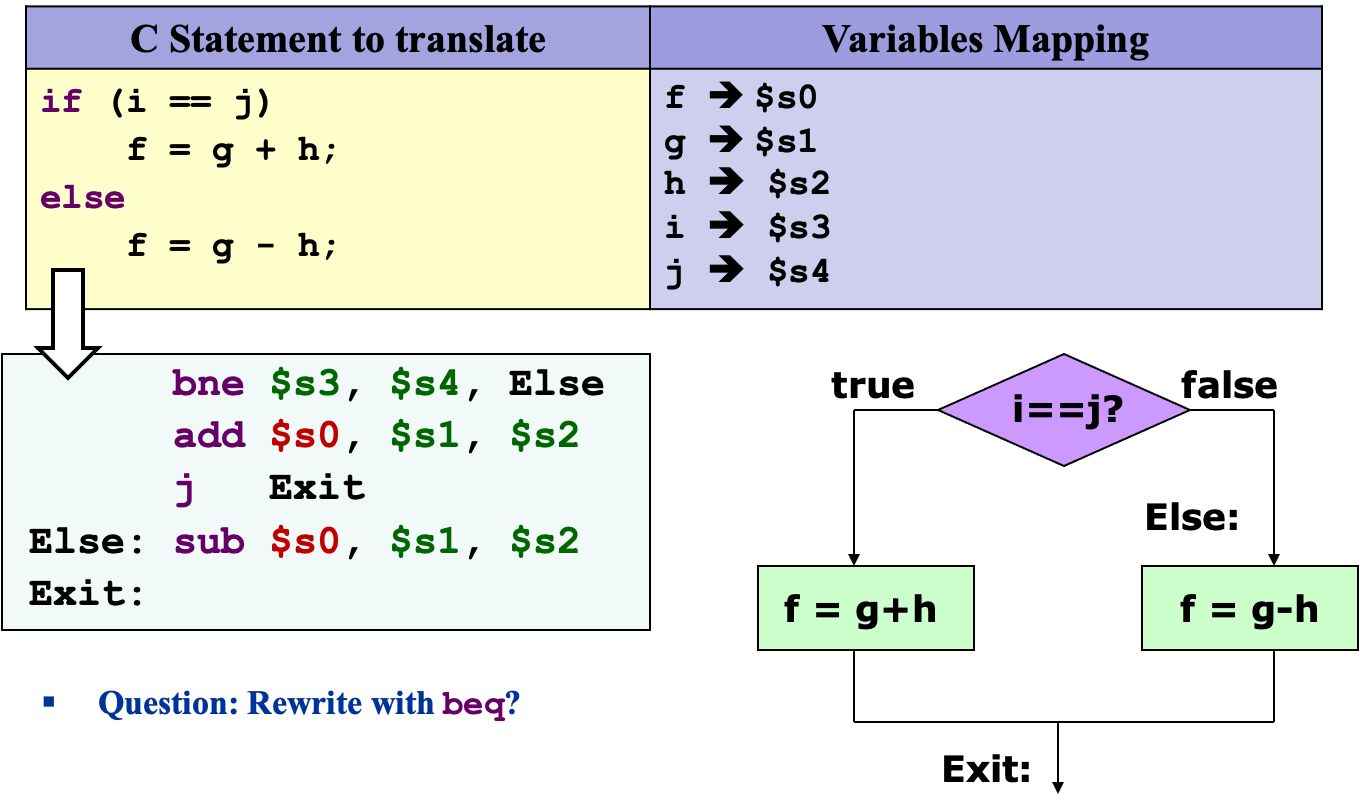
用beq重写beq $s3, $s4, Else sub $s0, $s1, $s2 j Exit Else: add $s0, $s1, $s2 Exit:- 1
- 2
- 3
- 4
- 5
练习
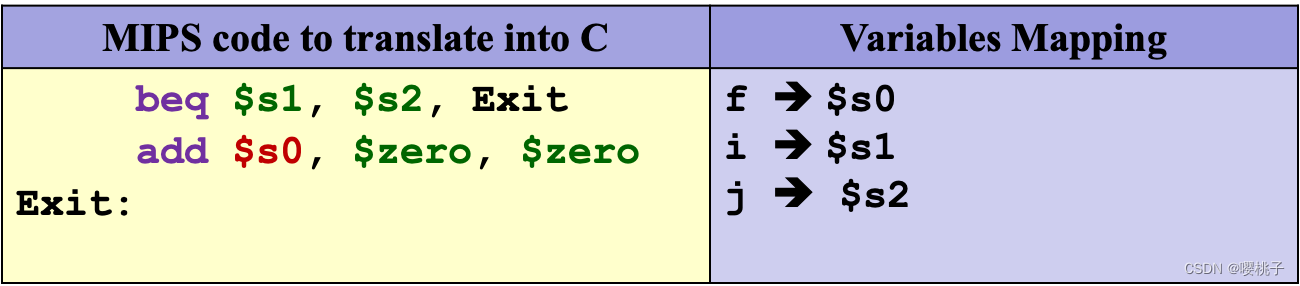
问以上编译代码的原始高级语言语句是什么?if(i == j) { f = 0; }- 1
- 2
- 3
3.4 循环
Loops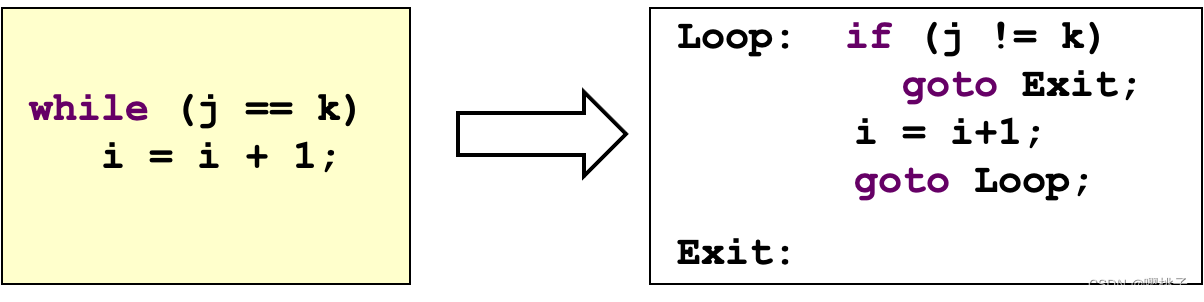
任何形式的循环都能在编译语言里用条件分支和跳转语句表示出来。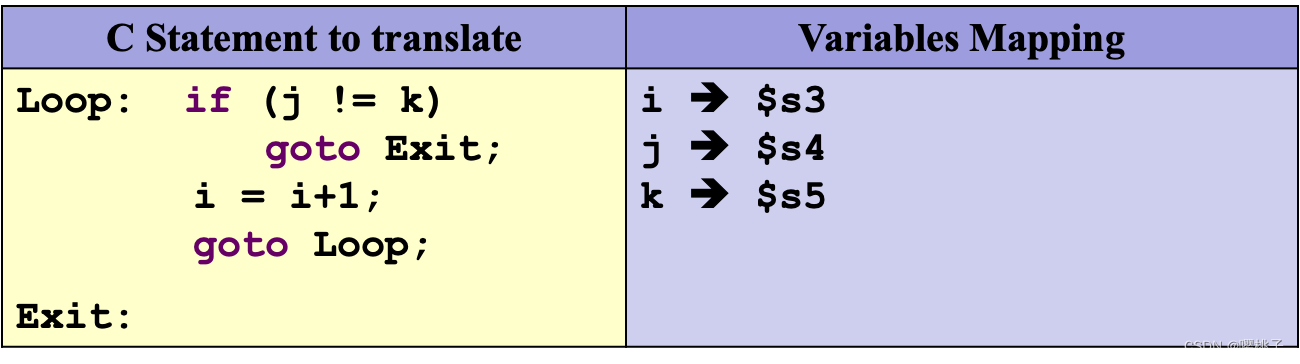
问:对应的MIPS代码是什么?Loop: bne $s4, $s5, Exit add $s3, $s3, 1 j Loop Exit:- 1
- 2
- 3
- 4
练习

写出以上循环语句的MIPS指令add $s0, $zero, $zero addi $s1, $zero, 10 Loop: beq $s0, $s1, Exit addi $s2, $s2, 5 addi $s0, $s0, 1 j Loop Exit:- 1
- 2
- 3
- 4
- 5
- 6
- 7
不等式
我们有了beq和bne,有没有“如果小于,进入分支”(brach-if-less-than,blt)呢?
实际上是没有blt的,需要使用slt(set on less than)或者slti来构造。
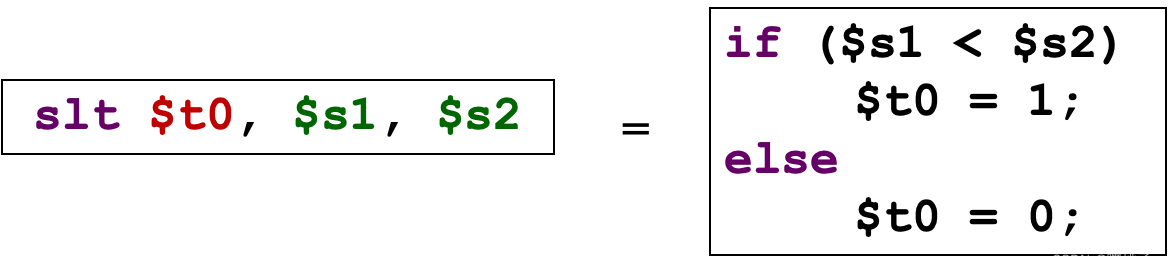
构造一个blt $s1, $s2, L的指令:
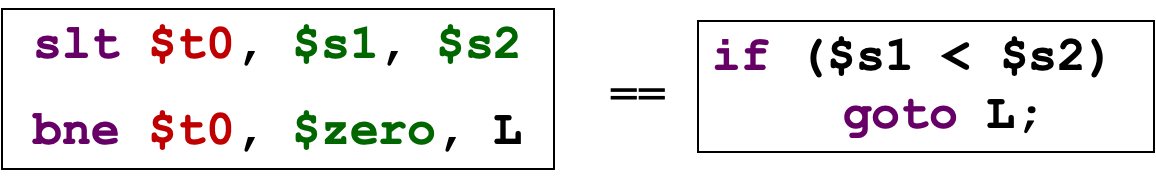
blt也是一个伪指令,编译器会把它转化为两行等式代码。3.5 数组和循环
Array and Loop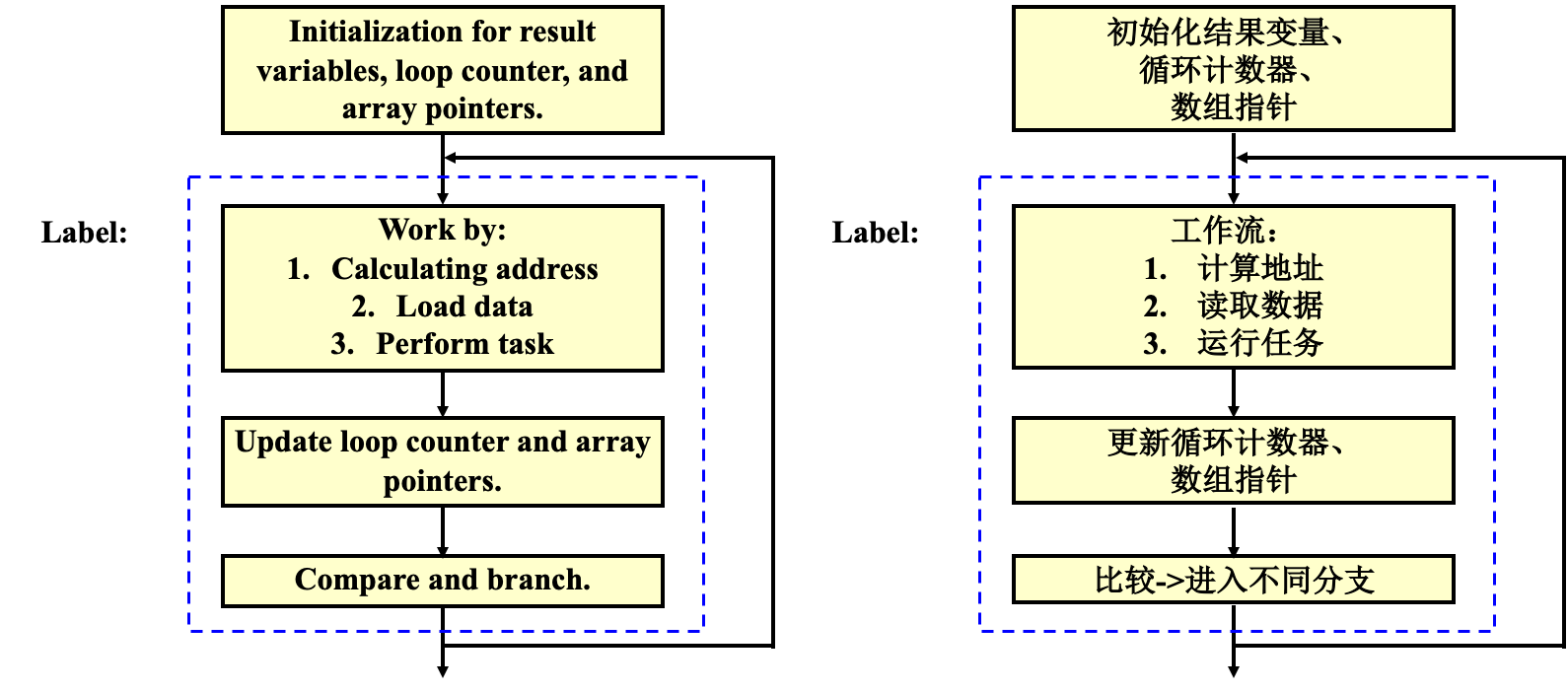
问题:如何计算数组A中0的个数?
- A是一个有40个元素的、以word为单位的数组。
- A[]的地址 ->
$t0,结果存储在$t8
// 简单的C语言代码 result = 0; i = 0; while (i < 40) { if (A[i] == 0) result++; i++; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Address of A[] -> $t0
Result -> $t8
i -> $t1编译 方法一:
addi $t8, $zero, 0 # 初始化结果变量 addi $t1, $zero, 0 # 初始化数组指针 addi $t2, $zero, 40 # 确定数组终止位置 Loop: bge $t1, $t2, end # 如果当前数组指针大于数组终止位置,跳出循环 sll $t3, $t1, 2 # i * 4 (指针向下移动四位) add $t4, $t0, $t3 # &A[i] 计算基地址加上偏移量后目标值的位置 lw $t5, 0($t4) # $t3 <- A[i] 读取地址指针在t4位置上数组的值,赋给t3 bne $t5, $zero, skip # 如果A[i] != 0,跳过 addi $t8, $t8, 1 # 如果A[i] == 0,结果++ skip: addi $t1, $t1, 1 # i++ j loop # 下一轮循环 end:- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
Address of A[] -> $t0
Result -> $t8
i -> $t1
编译 方法二:用指针addi $s8, $zero, 0 # 初始化结果变量 addi $t1, $t0, 0 # i + 基地址:当前元素的地址 addi $t2, $t0, 160 # $t2 <- 基地址 + 160 (&A[40]) loop: bge $t1, $t2, end # 如果当前数组指针大于数组终止位置,跳出循环 lw $t3, 0($t1) # $t3 <- A[i] 将A[i]数值读取至t3 bne $t3, $zero, skip # if(A[i] != 0) 跳过 addi $t8, $t8, 1 # result++ skip: addi $t1, $t1, 4 # 转移到下一个元素(A[i]地址+4 -> A[i+1]的地址) j loop end:- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
练习 #1
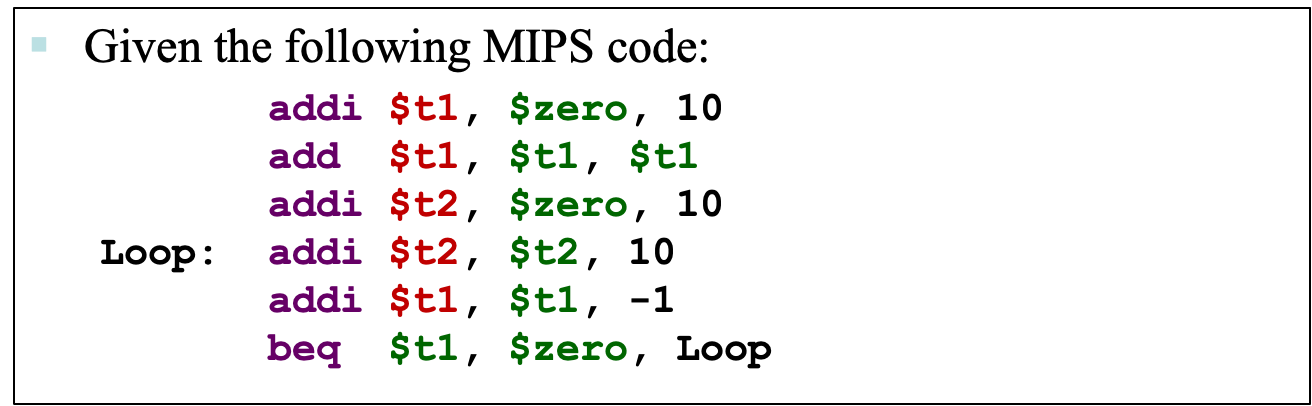
翻译一下(不是规范的C代码):
t1 = 10; t1 = t1 + t1 = 20; t2 = 0 + 10 = 10; do{ t2 = t2 + 10; // 10 + 10 = 20 t1 = t1 - 1; } while(t1 == 0); // 此时t1==9,不用下一轮- 1
- 2
- 3
- 4
- 5
- 6
- 7
1. 有多少指令被执行了? 6行。
2.$t2的最终结果是多少? 20。练习 #2
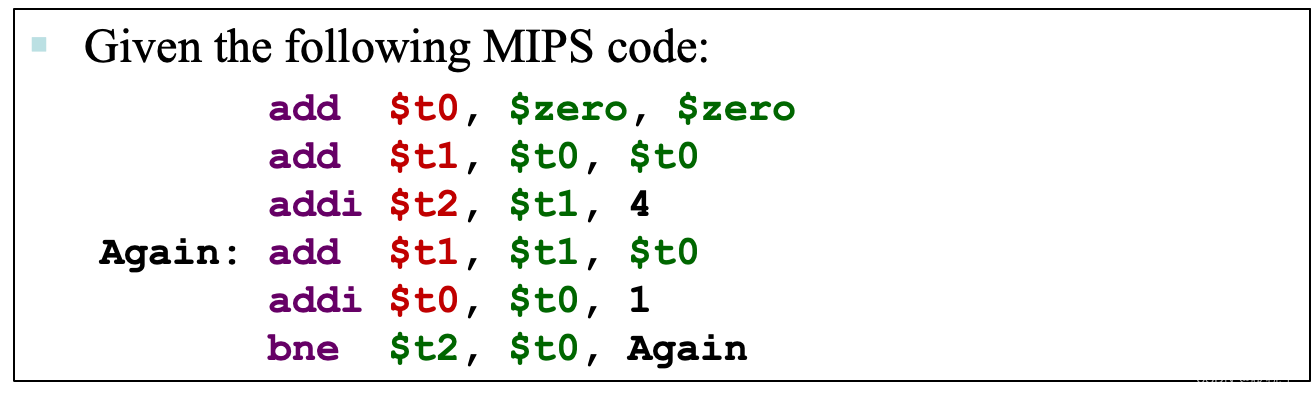
翻译一下(不是规范的C代码):
t0 = 0 + 0 = 0; t1 = t0 + t0 = 0 + 0 = 0; t2 = t1 + 4 = 0 + 4 = 4; do{ t1 = t1 + t0; // t1 = 0 -> 0 + 1 -> 1 + 2 -> 3 + 3 -> 6 + 4 t0++; // t0 = 1 -> 2 -> 3 -> 4(这三行走多少遍就看t0什么时候加到t2(4) -》走4次结束) } while(t2 != t0) // 4 != 1 ->- 1
- 2
- 3
- 4
- 5
- 6
- 7
1. 有多少指令被执行了? 3 + 4 * 3 = 15
2.$t1的最终结果是多少? 10练习 #3
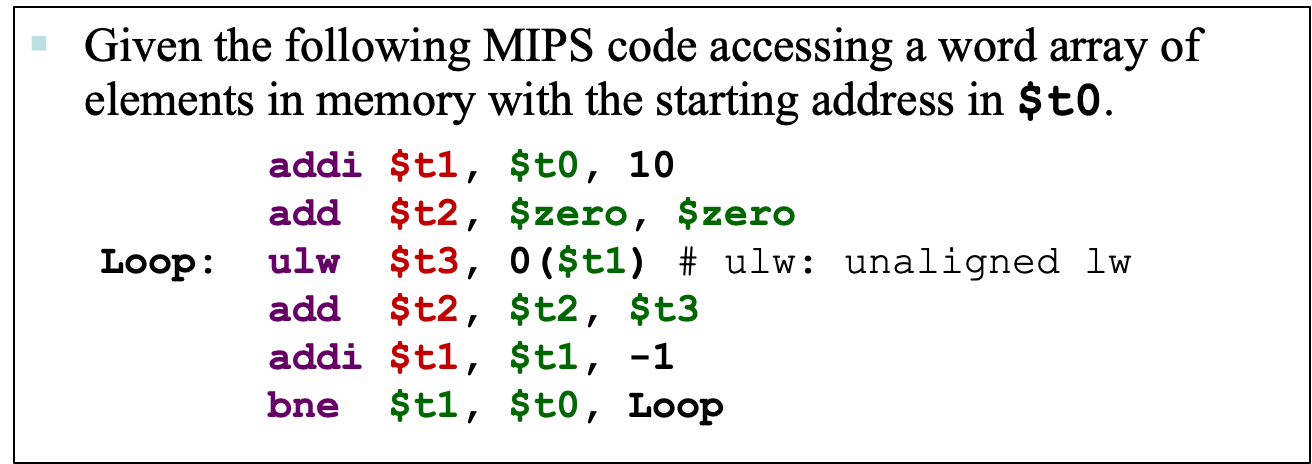
翻译一下(不是规范的C代码):
t0:word数组的初始地址t1 = t0 + 10 // 初始地址下移10个字节 t2 = 0 do { t3 = A[]初始地址下移10个字节的地址里存的值 t2 += t3 // t2加上上面这个值 t1--; // 地址指针上移一位 } while(t1 != t0) // 当地址指针到数组头地址前,继续循环- 1
- 2
- 3
- 4
- 5
- 6
- 7
1. bne指令会执行多少次? 从9到0,10次。
2. 有多少次bne跳进了 label loop分支? 9次。10次中除了最后一次相等了,其他都会跳回去。
3. 有多少指令被执行了? 2 + 4 * 10 = 42
4. 有多少单一的字节被读取了read from memory? 13。每次读4个,读到t0的时候会读多3个其他的。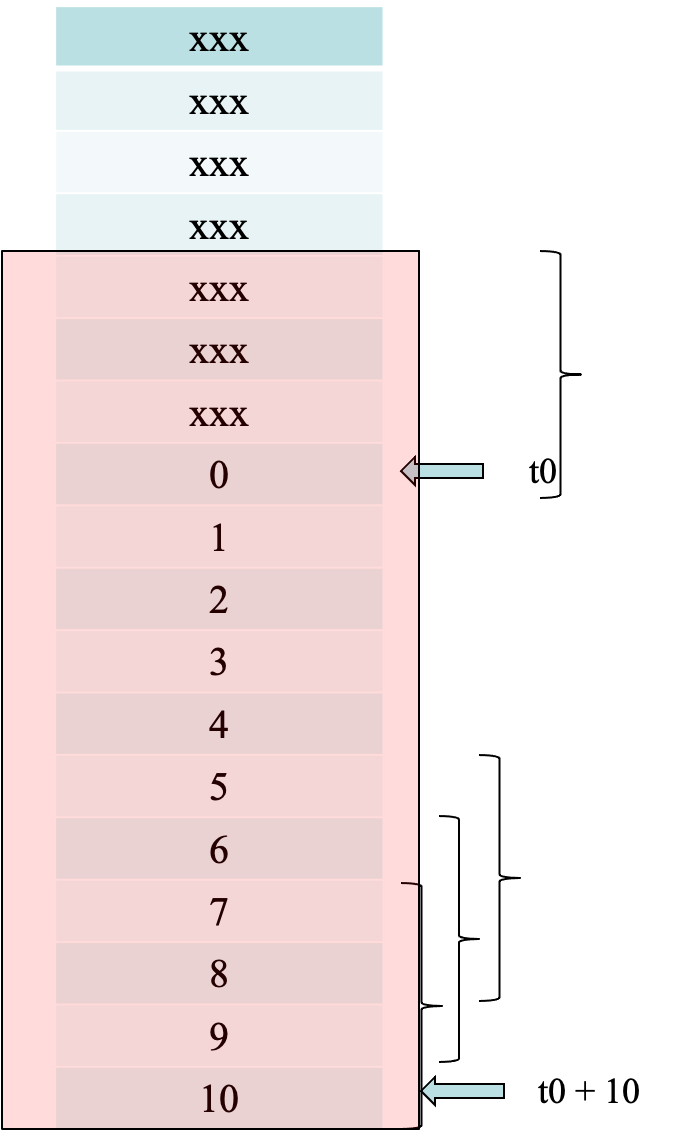
4. MIPS III 指令格式
4.1 Overview
- 编译指令在执行实际操作时会被翻译为机器指令。接下来将分析如何将MIPS编译指令转化为二进制形式。
- 解释为什么指令中常数最多16bits,位移一次最多5bits。
4.2 MIPS编码
MIPS Encoding- 每个MIPS指令为32 bits定长。一个操作的所有信息都需要在这32bits里表达。
- 其他的挑战:为了降低处理器设计的复杂程度,指令编码应该尽可能的普通,也就是包含尽可能少的格式,越少不一样的越好。
4.3 MIPS 指令区分
MIPS Instruction Classification指令通过操作数区分:

4.4 MIPS 寄存器 (同2.4)

4.5 R-Format

这类指令的二进制格式为(数值表示当前区块被分配了多少个二进制位):
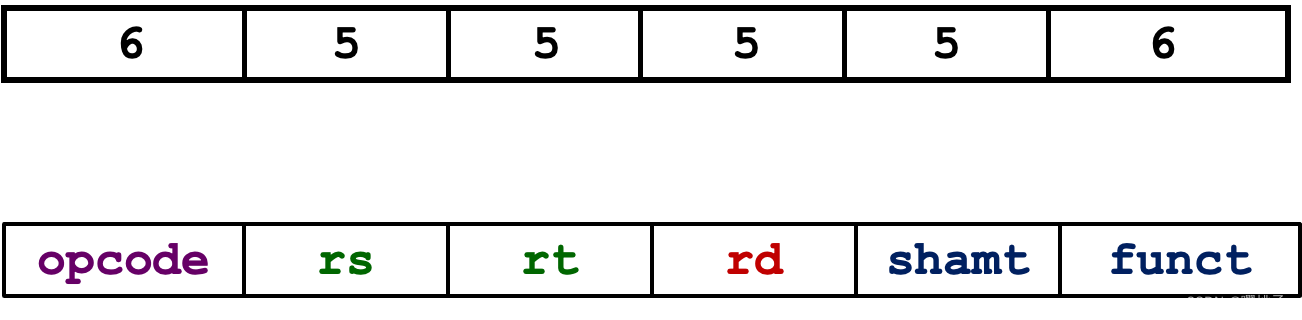
每一块都是一个独立的5或6比特的无符号整数 。- 5 bits的区块可以表示任意0-31的整数
- 6 bits的区块可以表示任意0-63的整数
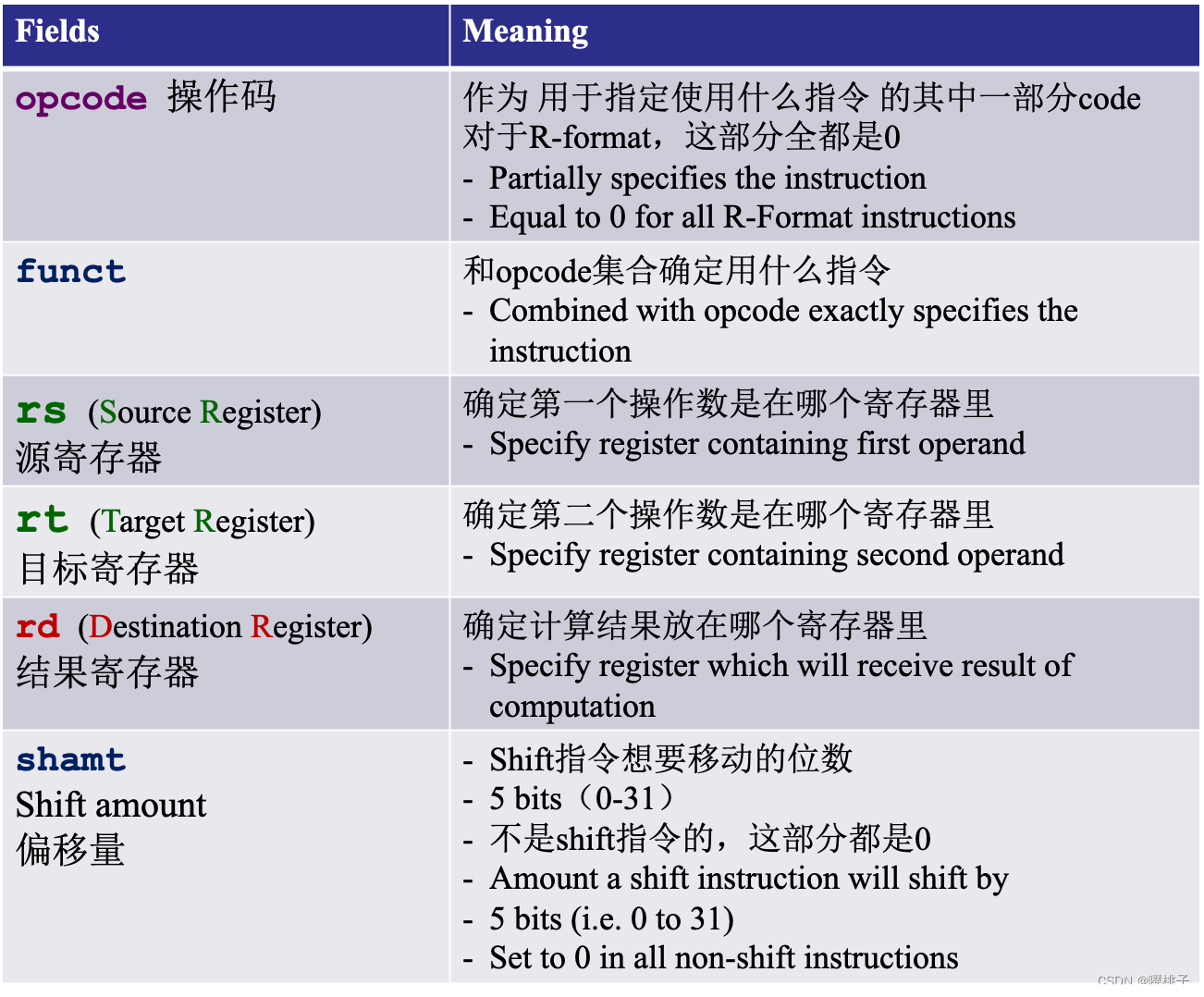
例子 #1
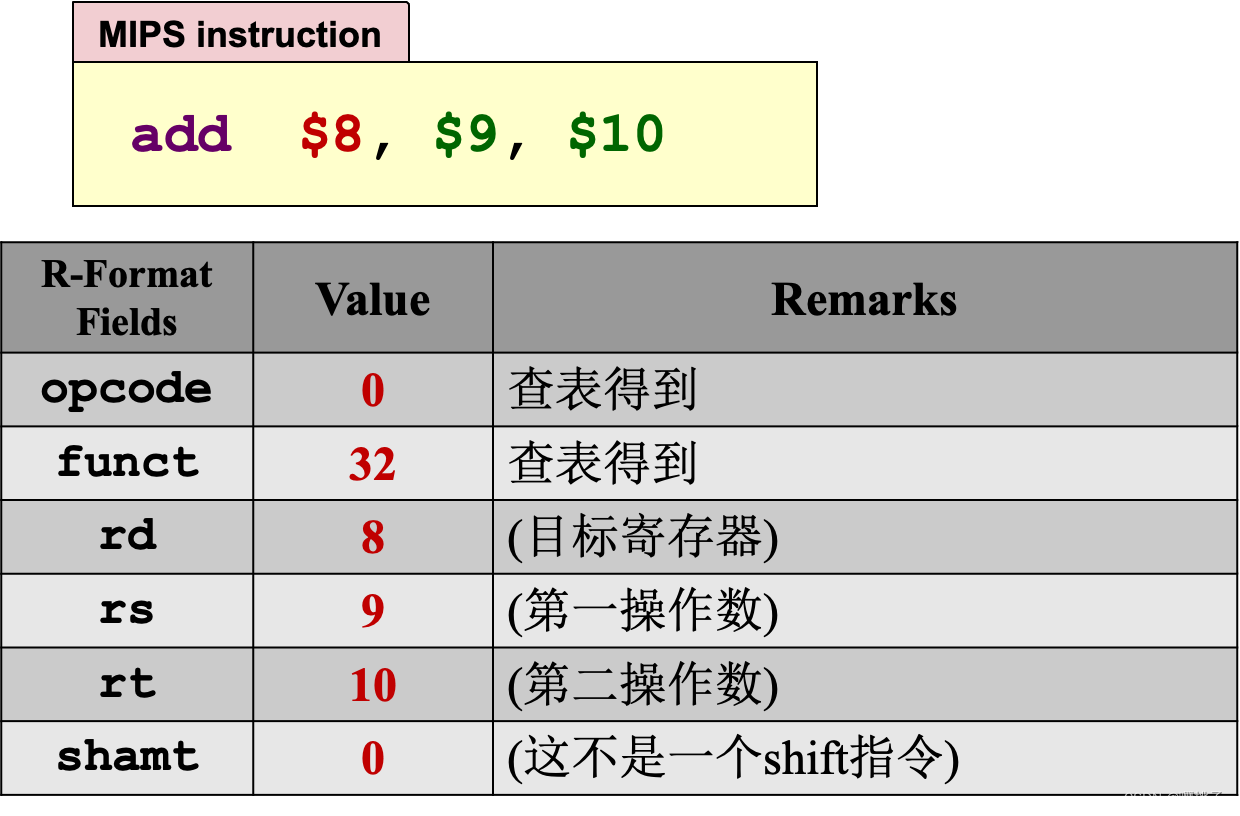
-
先用十进制表示

-
转换成二进制表示

-
把他们按四位一划分,再用16进制表示

例子 #2

-
先用十进制表示

-
转换成二进制表示

-
把他们按四位一划分,再用16进制表示

例子 #3

- 先用十进制表示
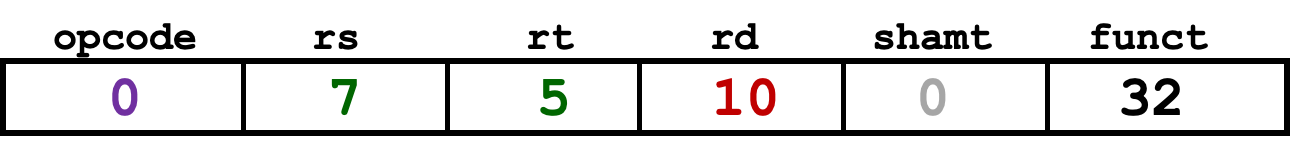
- 转换成二进制表示
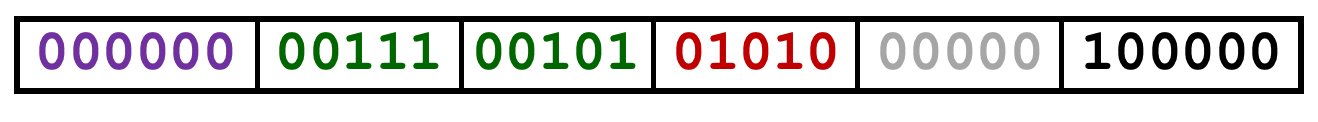
- 把他们按四位一划分,再用16进制表示
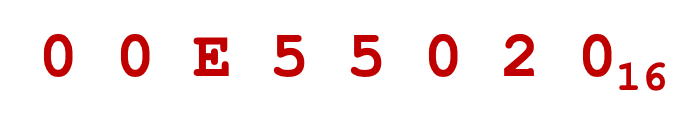
4.6 I-Format
4.6.1 基础结构
- 有常量的指令如何设计?
- 5-bit的位移区域
shamt只能表示0-31 - 常量可能比这个大得多
- 例如,lw,sw指令需要更大的偏移量offset
- 5-bit的位移区域
- 折中做法:定义一个新的格式,只有一部分和R-format一样。
- 如果指令中有常数,最多使用2个寄存器。

这类指令的二进制格式为(数值表示当前区块被分配了多少个二进制位):
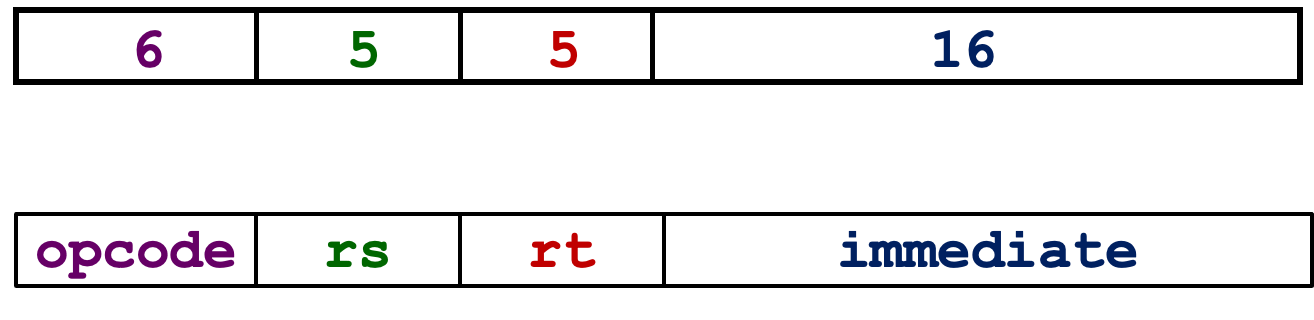
opcode、rs、rt和在r-format的位置是一样的。opcode:由于没有funct的位置,这里的opcode单独确定一个指令。rs:确定源寄存器rt:确定接收结果的寄存器(r-format里面是用rd接收)immediate:- 这是一个
有符号的整数,16bits ->表示最多 2 1 6 2^16 216个不同的数字。 - 足够大去表示:
lw / sw中的偏移量- 大多数在
addi / subi / slti指令中的数值
- 这是一个
例子 #1

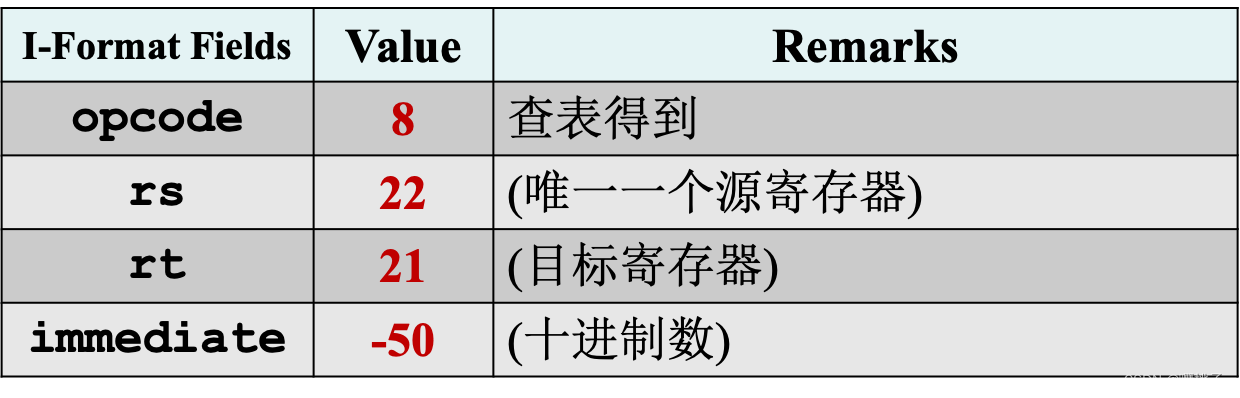
-
先用十进制表示
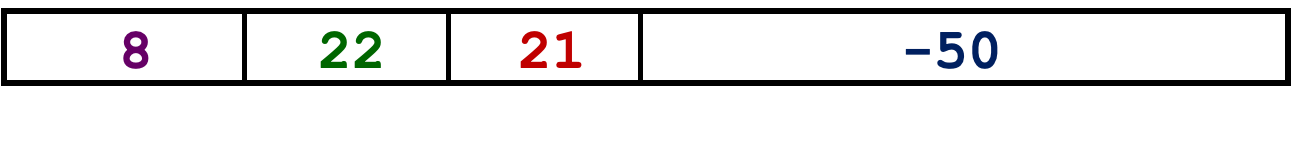
-
转换成二进制表示
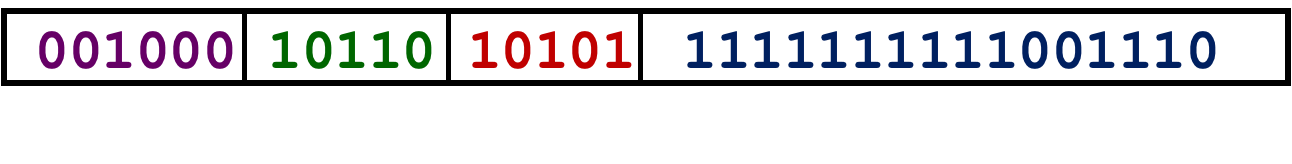
-
把他们按四位一划分,再用16进制表示

例子 #2

-
先用十进制表示

-
转换成二进制表示

-
把他们按四位一划分,再用16进制表示

4.6.2 指令地址
- 指令是存放在内存中的,所以他们也有地址。
- 控制流指令会使用到这些地址 (
beq / bne / j)
- 控制流指令会使用到这些地址 (
- 因为指令是32-bit长的,指令地址也是word-aligned的。
程序计数器
Program Counter (PC):一个用于记录在处理器中执行的指令地址的特殊寄存器。4.6.3 分支:程序计数器相对寻址
PC-Relative Addressing
-
opcode:指定beq或bne -
rs 、 rt:确定要参与比较的寄存器 -
immediate:内存的地址有32bits,immediate只有16bits,不够表示整个目标地址(绝对地址)。-
条件分支语句 if-else / while / for,通常循环的内容都比较少,最多50行指令。(注意jump不是分支语句)
-
总结:分支通常和程序计数器的位置差不太多。
-
解决方法:根据相对于PC的偏移量,确定目标地址
目标地址 = PC + immediate(immediate是一个有符号 2s complement整数)- 分支可以放在距离PC
±
2
15
\pm 2^{15}
±215字节的位置,对于大多数循环,这就够用了。

-
-
分支计算

- 注意点
immediate表示要跳多少个words,这个是和需要跳掉的指令数一样的immediate可正可负- 根据硬件的设计,应该将immediate和(PC+4)相加,而不是和PC相加。
- 注意点
例子 #1


immediate是要对当前PC加/减多少个指令数(从当前指令结束地址开始,进入分支)。- 例子中 immediate = 3
End = (PC + 4) + (immediate * 4)
所以,
- 先用十进制表示

- 再用二进制位表示

例子 #2

此时的immediate为-4。(因为第四条已经走完了,要往回走四个指令才到第一条指令头)4.7 J-Format
- 对于分支,我们使用了相对PC寻址方式,因为我们的分支不会离得太远。
- 对于jump,我们却可能跳到内存中的任何一个地方。
- 理想情况下,我们应该可以跳到32-bit内存地址的任何一个位置上。但我们实际上不能这么做(因为一条指令只有32位,全给地址了,就没法放opcode了)。


- 理想情况下,我们应该可以跳到32-bit内存地址的任何一个位置上。但我们实际上不能这么做(因为一条指令只有32位,全给地址了,就没法放opcode了)。
- 保持六位的opcode不变,保持和r-format和i-format一致。
- 其他的26位全部放目标地址
- 但这仍然只有26位?
- 就像分支branch一样,jump同样只能跳转到word-aligned的地址,所以最后两位永远是00,所以可以假设最后两位是00,后面找的时候再补上。-> 相当于现在有28位了,还剩下4位。
- MIPS选择从
PC+4中获得这四位比特位。 ⇒ 这意味着我们其实不能访问内存中的任何位置,但这在大多数情况下都足够了。 - 综上,跳转的最大范围是多少呢?256MB的范围。
- 1 M B = 2 20 1MB = 2^{20} 1MB=220
- 2 28 = 2 8 ∗ 2 20 = 256 M B 2^{28} = 2^8 * 2^{20} = 256MB 228=28∗220=256MB
- 如果需要跳到超过256MB范围的地方怎么办?使用
jr指令,jump-to- register,跳到某个寄存器,目标地址会用整个寄存器来保存。
- 但这仍然只有26位?

例子
如果在i-format的语句中,想要跳转到超过16bits地址的位置怎么办?如
beq $s0, $s1, L1,其中L1超过了PC可以支持的范围。
参考StackOverflow答案如果 I-format 命令的 16 位对于 L1 来说还不够,您可以使用 J-format,因为它有 26 位用于您的地址(只需围绕它构建您的 if)。
如果这还不够,您应该使用以下命令将地址保存到寄存器中:la $t0, L1然后使用以下命令跳转到该寄存器:jr $t0如果您首先将其安全地保存到寄存器中,那么您将拥有完整的 32 位地址。4.8 寻址方式
- 寄存器寻址
Register addressing:操作数是寄存器。

- 常数寻址
Immediate addressing:操作数是一个位于指令内的常量。

- 基址寻址(位移寻址)
base addressing (displacement addressing):操作数在【一个寄存器 + 指令里的一个常数】所映射的内存地址里。(如lw和sw)

- 程序计数器相对寻址
PC-relative addressing:【PC + 指令里的一个常数】(如beq和bne)

- 伪直接寻址
Pseudo-direct addressing:【PC的前四位】+【指令里的26位地址】+【00】

总结
每条MIPS指令由32位比特组成

- branch和load/store都是i-format的指令
- branch使用PC- relative寻址
- load/store使用基地址寻址
- branch和jump
- branch使用PC- relative寻址
- jumps使用伪直接寻址
pseudo-direct addressing
- Shift
- Shift位移使用r-format指令,但是其他的常数指令(addi、andi、ori)使用i-format

5. 数据路径设计
DataPath Design5.1 建立一个处理器:数据路径和控制
Building a Processor: Datapath & Control处理器中两个核心组成部分:
- 数据流
Datapath- 处理数据的部件集合
- 进行算术、逻辑、内存运算
- 控制流
Control- 根据程序指令,告诉数据流/内存/IO设备他们应该做什么
5.2 MIPS处理器的实现
MIPS Processor: Implementation核心MIPS ISA子集的最简单实现应该包括:
- 算术运算和逻辑运算: add, sub, and, or, addi, andi, ori, slt
- 数据传输指令:lw, sw
- 分支:beq, bne
(位运算指令 sll/srl等和J-type指令这里不做讨论)
5.3 基础指令处理循环
Instruction Execution Cycle (Basic)
- 获取指令
Fetch instructions- 从内存中获取指令
- 地址在程序计数器寄存器(PC register)中找到
- 解码操作
Decode operation- 找出应该做什么操作
- 获取操作数
Operand Fetch- 获取操作所需的操作数
- 执行操作
Execute- 执行要求的操作
- 存储结果
Result Write- 将操作的结果存储起来
5.4 MIPS指令执行
MIPS Instruction Execution下面展示了三种MIPS代表性的指令的实施步骤(获取和解码的步骤没有展示,假设已按标准流程处理):

opr = operand
ofst = offset
MemAddr = Memory Address另一种设计:
- 合并
解码和获取操作数的过程(解码在MIPS中比较简单) - 将
执行过程分成ALU(计算Calculation)和内存读取Memory Access

维基百科
ALU: 在计算中,算术逻辑单元( ALU ) 是一种组合 数字电路,它对整数二进制数执行算术和按位运算。5.5 构造一个MIPS处理器
Build a MIPS Processor我们要做的事:
- 找出每个步骤的要求和过程
- 抽象出一个高阶的流程图,再对每一块元素细致展开
- 基于基础的设计,看看是否不同的指令都能被正确处理(可以根据需要修改)
5.5.1 指令获取阶段
Fetch Stage要求
Requirements指令获取阶段
- 使用程序计数器PC从内存中获取指令
- PC是处理器里的一种特殊的寄存器
- 要找下一个指令地址时,PC+=4
- 我们是怎么知道下一个指令时在PC+4的位置的?
- 注意branch/jump指令执行时是例外的
输出到下一阶段(解码
Decode)
- 指令会被执行
图中的各部分解释:-
指令内存
Instruction Memory- 用于存储指令
- 是一个时序电路
Sequential circuit(后面会解释) - 有一个存储信息的内部状态
- 假设已有时钟信号
Clock signal(图中没展示)
- 是一个时序电路
- 根据地址提供指令
- 输入给定的指令地址,内存输出在这个地址中的内容
- 抽象的概念化图示如下

- 用于存储指令
-
加法运算器
Adder

- 执行两数相加的组合逻辑
- 输入:两个32-bit数
A B - 输出:两数之和
A + B
- 输入:两个32-bit数
- 执行两数相加的组合逻辑
-
时钟的概念
- 看起来我们好像是在同一时间读取、更新程序计数器PC的。这样其实不能正确地工作。
- 实际上,我们是在前半段“时钟周期
clock period”读取程序计数器PC,然后在“下一个时钟的上升沿next rising clock edge”将其更新为PC+4(图中红色箭头)。(也就是没有看到上升信号之前,都不能把PC+4后的结果更新上去)

阅读资料:深入浅出计算机组成原理学习笔记
Clocking视频解读: Crash Course Computer Science - episode 7
Crash Course Computer Science - episode 85.5.2 解码阶段
Decode Stage- 指令解码阶段
- 从指令域中获取数据
-
- 读取
opcode,确定指令类型和域的长度
- 读取
-
- 从所需的寄存器读取数据【可以是两个寄存器(add)、一个寄存器(addi)或零个寄存器(j)】
-
- 从指令域中获取数据
- 从前一个阶段
Fetch得到输入,指令将会被执行 - 输出到下一个阶段
ALU,对操作数进行对应的操作。

组成元素:- 寄存器集合
Register File- 是有32个寄存器的集合
- 每个都有32-bit宽,可以通过确定寄存器数来读写;
- 一条指令最多读两个寄存器
- 一条指令最多写一个寄存器
RegWrite是一个控制信号- 它可以声明对一个寄存器的写入操作
- 1 (True) = Write,0(False)= No Write

- 是有32个寄存器的集合
R-format 指令

I-format 指令
如果按r-format的处理方式,读入的数据1/2应该是rs/rt的位置,而i-format的处理方式中,读入的数据应该是rs和immediate。
因此,如果不改变读取的索引,就会读错数据。

选择目标位置(要写入的寄存器是从哪几位看出来的)

多路复用器
Multiplexer- 功能:从多条输入线路中选择一条
- 输入:n条相同宽度的线路
- 控制信号:m个比特,其中 n = 2 m n = 2^m n=2m
- 输出:如果
control = i,选择第i个输入线路
维基百科
在电子技术(特别是数字电路)中,多路复用器(multiplexer / mux),也称为数据选择器(Data Selector),是一种可以从多个模拟或数字输入信号中选择一个信号进行输出的器件。
一个有 2 n 2^n 2n 输入端的数据选择器有 n 个可选择的输入-输出线路,可以通过控制端来选择其中一个信号被选择作为输出。
数据选择器主要用于增加一定量的时间和带宽内的可以通过网络发送的数据量。
选择数据2(immediate value)
这里的符号扩展
Sign Extend是什么意思?
因为要与之相加的数据1是32位的,而immediate value只有16位,因此要将其扩展为32位。
那么怎么才不会改变原有数据的信息呢?⇒ 扩展的比特等于该数字的符号位。
例如:-50 ⇒ ···· ···· ···· ···· 1110 0111 1010 0011 (符号位为第一个比特,即1) 扩展为32比特 1111 1111 1111 1111 1110 0111 1010 0011 +17 ⇒ ···· ···· ···· ···· 0000 0000 0000 1001 (符号位为第一个比特,即0) 扩展为32比特 0000 0000 0000 0000 0000 0000 0000 1001- 1
- 2
- 3
- 4
- 5
加了多路复用器之后,我们就可以让他来决定,读取的是
第二操作数(寄存器)(r-format)还是扩展为32比特的常量数immediate(i-format)。

读取字指令
Load Word Instruction第一个多路复用器选择rt作为写入的寄存器,第二个多路复用器选择扩展为32位的常量数和第一操作数(
$22,原始寄存器)做运算。

分支指令
Branch Instruction- 读入寄存器9和0。
- 因为这是一个i-format的指令,第一个多路复用器会选择
0读取写寄存器。但是我们不会在分支指令里执行写操作,所以这里没什么关系。 - 在第二个多路复用器中,对于一般的i-format指令,我们会选择
拓展为32位的常量数immediate输出,但在beq里,我们需要去比较$9和$0寄存器里的数(也就是read data 1 & 2),因此不能选择immediate,要选择read data2输出。 - 那没被第二个多路复用器选择的
3去哪了呢?⇒ 发给程序计数器PC了(在execute阶段会详细解读)。

5.5.3 ALU阶段
ALU Stage要求
Requirements- ALU阶段
- ALU:
Arithmetic-Logic Unit,算术逻辑单元 - 这个阶段也称为执行阶段
Execution stage - 执行多数以下指令的实际操作:
- 算术运算(add,sub),位运算(sll),逻辑运算(and,or)
- 内存操作(lw,sw):地址运算
- 分支操作(bne,beq):执行寄存器比较、目标地址计算
- ALU:
- 从上一阶段(Decode)获得输入:操作和操作数
- 输出到下一阶段(内存):计算的结果

ALU 是用于算术和逻辑运算的组合单元,它输入两个32-bit的数字,通过4-bit 的控制器来确定特定的运算,最后输出算术/逻辑运算的结果(有一个1-bit的信号来说明结果是不是0)。
非分支运算
non-branch instruction
在下面这个例子中,
- 我们假设9号寄存器(rs)里放着数字10,10号寄存器(rt)里放着数字12,那么读取寄存器1和2就会分别读入10、12;
- read data1为10,read data2为12;
- read data 2还要被多路复用器选择(此时ALUSrc置为0,选择12,而不是immediate value),最后输出12到ALU;
- ALU控制器置为
0010(根据上表可查得),将10和12相加,输出22 (ALU result) 和不为零(isZero?)。
ALUControl用的是opcode+func field。

分支运算
branch instruction分支运算比执行两数相加难得多。
例如,beq $9, $0, 3- 分支输出的结果:
- 使用ALU来比较寄存器的内容
- 使用1-bit的
isZero信号来表示两者是否相等(如果相等,isZero=1,否则为0)
- 分支目标地址
- 引入额外的逻辑来计算地址
- 需要程序计数器PC(从fetch stage获得)和偏移量OFFSET(从decode stage获得)
例子:

分支阶段运算步骤:- 从rs、rt读取到应该去
$9 $0两个寄存器取数,取到的数字为read data1和read data2。其中,read data1直接读入ALU,read data2还需要经过第二个复用器确认。第一个复用器确定当前不需要写入数据,将寄存器写标识RegWrite置为0。 - 由于此时为分支运算,ALUSrc被设为0,因此,不读入符号扩展后的immediate value,读入read data2。
- read data1和read data2在ALU中进行减运算sub(ALUControl指令为
0110),如果相减结果为0,说明两者相等,isZero置为1,否则置为0。 - 接下来是分支的地址运算,从immediate部分读取16-bit的数据,通过符号扩展为32-bit,经过左移两位的位运算
left shift 2-bit,得到4倍的immediate(4 * immediate),也即当前指令到达目标地址的word位移*4(乘以四换成byte),此时再加上当前指令的下一条指令地址(PC+4)的绝对地址,就得到目标地址的绝对地址了。⇒ 也就是说,目标地址的绝对地址为(PC+4) + immediate * 4。 - 但是我们有条件成立(跳转到目标地址)和条件不成立(继续执行下一条指令)两种情况,所以还需要第三个复用器来判断。令此时的
PCSrc等于isZero的值 (⚠️注意PCSrc不是和isZero直接连起来的,只是在beq指令下他们相等,否则执行bne的时候就会出错了) ,
(1)如果isZero == 1,两者相等,条件成立 ⇒ PCSrc == 1 ,复用器选择immediate*4和PC+4相加的结果,跳转到目标地址((PC+4) + immediate * 4);
(2)如果isZero== 0,两者不等,条件不成立 ⇒ PCSrc == 0 ,复用器选择PC+4,跳转到下一条指令。
5.5.4 内存阶段
Memory Stage- 内存访问阶段:
- 只有读取load和存储store指令需要执行这个阶段
- 使用ALU stage计算的内存地址
- 从内存中读取数据,或写入数据到内存
- 其他的指令保持idle
- 从ALU stage得到的结果会直接跳过,然后到写入寄存器阶段
Register Write
- 从ALU stage得到的结果会直接跳过,然后到写入寄存器阶段
- 只有读取load和存储store指令需要执行这个阶段
- 从前一个阶段(ALU stage)输入:计算得到的内存地址结果
- 输出到下一个阶段(
Register Write):结果会被存储起来。

- 我们从ALU stage读取到一个32-bit的地址数据,一个32-bit的写入数据。
- 如果此时
MemWrite = 1, MemRead = 0,此时会将write date写入到目标地址 - 如果此时
MemWrite = 0, MemRead = 1,此时会从目标地址读取数据
- 如果此时
读取
load instruction例子,
lw $21, -50($22)

步骤:
假设22号寄存器里存着数字98,21号寄存器里存着数字15。- rs为22,从22号寄存器read register1中读取数据read data1,rt为21,此时RegDst置为0,将write register设为21号寄存器。
- immediate value为16bit的-50,经过符号扩展为32bit的-50,此时ALUSrc=1,第二个复用器选择-50(而不是read data2,即21号寄存器里存的数字15)。
- 将22号寄存器中的数字98和-50放入ALU,相加得到48,将48作为目的地址,此时
MemWrite = 0, MemRead = 1,执行内存读取,将48读到写寄存器$21(write register $21)。
写入
write instruction
步骤:
假设22号寄存器里存着数字98,21号寄存器里存着数字15。我们要把21号寄存器的内容存到-50+[$22] = 48的内存地址中。- rs是22,rt是21。$22作为read register1,$21作为read register2(虽然没啥用,但是由于这些操作都是在实际的电路上进行的,所以你只能选择后面不要某条路传来的数据,不能阻止它传进来)和write register,此时没有需要写入寄存器的操作所以
RegWrite = 0。read data1为read register1里的数据98,read data2 为 read register2里的数据15, read data2传到数据内存中的write data。 - 此时第二个复用器中
ALUSrc = 1,选择符号拓展后的32-bit immediate value -50 - 将-50和98传入ALU,相加得到48,作为目的地址。
- 此时
MemWrite = 1, MemRead = 0,执行写入内存的操作,将数字15写入内存地址48。
非内存指令
Non-Memory Instruction
步骤:
假设9号寄存器里存着数字12,10号寄存器里存着数字27。- rs为9,rt为10,rd为8。read register 1为9号寄存器,读入read data1 为9号寄存器里存着的数字12,read register 2为10号寄存器,读入read data2 为10号寄存器里存着的数字27。rd为8,第一个复用器中
RegDst = 1,即选择rd作为写入的寄存器write register。 - 第二个寄存器在符号扩展后的32-bit 前16位数字 和 read data2中,选择read data 2(
ALUSrc = 0) - 将read data1和read data2传入ALU,得到一个地址(但不会用到),此时
MemWrite = 0, MemRead = 0,不做任何操作。 - 另外将结果传到第三个复用器,第三个复用器会选择是否将内存中的数据读入寄存器,此时
MemReg = 0,不读入,而是选择ALU计算的结果。【注意,这个复用器MUX是倒过来放的,其他MUX都是上面是0下面是1,它是上面为1下面为0。】
5.5.5 寄存器写入阶段
Register Write Stage- 寄存器写入阶段
- 多数指令会将结果写入一个寄存器
- 比如算术运算、逻辑运算、位移运算、读取、设为更小set-less-than
- 需要一个目标寄存器和计算的结果
- 不需要写入寄存器的有:写入、分支、跳转
- 没有什么需要写入寄存器的结果
- 这些指令在这个阶段就啥也不做
- 多数指令会将结果写入一个寄存器
- 从前一阶段(memory stage)得到的输入:从memory或ALU得到的计算结果

- 结果写入寄存器阶段没有额外的元件
- 就是将正确的结果放到寄存器里
- 写入哪个寄存器是由decode stage决定的
Routing

步骤:
假设9号寄存器里存着的数字是10,10号寄存器里存着的数字是12。- rs为9,rt为10,rd为8。read register1为9,read register2为10, read data1为10,read data2为12;第一个复用器选择rd(8号)为写入寄存器write register。
- 第二个复用器
ALUSrc = 0,选择read data2传给ALU,与read data1进行加法运算。得到结果10+12=22。 - 此时
MemWrite = 0, MemRead = 0,不对数据内存做任何操作,将一个未知的数据传给第三个复用器,22也传给第三个复用器。 - 此时第三个复用器
MemToReg = 0,不将数据从内存写入寄存器,而是选择22,传给write data,写入write register。
5.6 完整的数据路径
The Complete Datapath
6. 处理器控制
Processor Control6.1 识别一些控制信号
Identidied Control Signals
6.2 生成控制信号
Generating Control Signals: Idea控制信号是根据要执行的指令生成的:
-
opcode -> 指令格式
-
例子:R-format指令 ⇒
RegDst = 1(使用Inst[15:11]) -
R-type指令有一些其他的信息:6-bit的
funct域(function code,Inst[5:0]) -
Idea:设计一个组合电路
combinational circuit来根据opcode (也有可能有function code)生成这些信号——这需要一个控制单元- 组合电路:输入会立即影响输出
- 时序电路:输入不会立即影响输出,而是会在特定的节点输出
6.3 控制单元
The Control Unit
控制单元就是用来控制这些“选择”的。实现控制单元的方法:
- 注意要实现的指令子集:操作码和功能码(如果适用)
- 遍历每个信号:根据指令操作码和/或功能码观察信号是如何产生的
- 构造真值表
- 使用逻辑门设计控制单元
6.4 控制信号
Control Signals回顾一下之前的一些MIPS指令集:

1 - 控制信号:
RegDst要写入哪个寄存器
- False (0):Write register = Inst[ 20 : 16 ]
- True (1):Write register = Inst [15: 11]

控制信号:
RegWrite是否写入寄存器
- False(0): no register write
- True(1): new value will be writtern

控制信号:
ALUSrc- False (0): Operand2 = Register Read Data 2:读取到的数据2
- True (1): Operand2 = SignExt(Inst[15:0]) :选择符号扩展后的32bit常数

控制信号:
MemRead- False(0) : 不进行内存读取操作
- True(1):使用地址读取内存数据

控制信号:
MemWrite- False(0) : 不进行内存写入操作
- True(1):将数据写入内存中的对应地址

控制信号:
MemToReg- True(1):register write data = memory read data 选择内存读出来的数据
- False(0):register write data = ALU result 选择ALU计算出来的结果
注意这里的MUX是倒过来放的。

控制信号:
PCSrc- “isZero?” 来自 ALU 的信号为我们提供了实际的分支结果(采用/未采用)
- False(0) :Next PC = PC + 4
- True(1):Next PC = SignExt(Inst[15:0]) << 2 + (PC + 4) = immediate * 4 + (PC + 4)

小结
现在还有ALUControl信号没讨论,下一节会说到。
现在得到的结论有:- 现在讨论的这几个信号可以通过opcode直接获得(function code还没有用到)
- controller的主要的几个部分可以指根据opcode来构建

6.5 ALUControl信号
ALUControl Signal我们进一步观察 ALU:
- ALU是一个组合电路:可以执行多项算术运算操作
- MIPS指令由一系列数字制定function

一个简单的、只考虑一个bit的MIPS ALU可以这样实现:
需要4个控制bits: Ainvert:当此值为1时,对A取反Binvert:当此值为1时,对B取反Operation:2个bit,选择三个结果的其中之一






了解了一位bit的ALU如何设计,我们将其抽象成一个黑箱,再去看看四位bit的ALU如何设计?把四个1-bit ALU串起来:
例1: A + B

例二:A - B

理解了4-bit ALU如何设计后,将其推广至32-bit也是一个道理。
层层解剖如何设计一个ALUControl信号
好了,现在我们可以开始设计
ALUControl信号了,设计它需要【6-bit 的 opcode区域和6-bit 的 function code区域】。- 暴力的思路是:我们可以直接用opcode和function code,也就是说,我们要用一个12个变量的表达式(6+6=12bits)。
- 多层级解析的方法是:
- 只是用输入的一部分,从而减少可能的方案数量,同时得到完整的输出;
- 简化设计流程,减少主要的controller的大小,从本质上提高电路的效率。
【1. 中间信号:
ALUop】首先我们有个简单的想法:
1. 使用opcode来生成一个2-bit的ALUop信号,用于表示指令属于哪一种类型(内存/分支/r-type)

2. 使用ALUop信号和function code域(这个只有r-type要用到)来生成4-bit的ALUControl信号。
【2. 生成
ALUControl信号】lw/sw:对于内存指令,我们不需要关注function code。我们需要将rs中的值和immediate相加得到地址,因此ALU的操作是add,ALUcontrol的信号则应该为0010(见右下的表)。beq:对于分支指令beq,我们也不需要关注function code。我们需要将两寄存器中的值相减,以比较二者是否相等,因此ALU的操作是subtract,ALUcontrol的信号则应该为0110。R-type:对于r-type类型的指令,他想要做什么操作,就可以对应查MIPS指令表得到对应的操作控制信号。比如想要相加,ALUcontrol的信号则应该为0010。

【3. 设计
ALU Control Unit】- input: 6-bit
functfield and 2-bitALUop - output: 4-bit ALUcontrol
我们要寻找一种最简单的表达式,来通过input确定唯一的output。(表中的X表示我们不用关心这里的值是什么)

ALUControl_i表示第i位的ALUControl信号如何表示(注意,i是从右到左的 ⇒ 图中顺序是3 2 1 0),a'表示对该数取反,a · b表示a and b,a + b表示a or b。ALUControl_3 = 0 ALUControl_2 = ALUop_0 + (ALUop_1 · F1)= ALUop_0 || (ALUop_1 && F1) ALUControl_1 = (ALUop_1' · F2)' = ALUop_1' or F2' = -ALUop_1 or -F2 = 第一位op取反 or 第二位F取反 ALUControl_0 = (ALUop_1 · (F0 + F3)) = ALUop_1 && (F0 || F3) = ALUop_1为1 同时F0 F3其中一个为1- 1
- 2
- 3
- 4
从而,我们得到简单的组合逻辑:

举例:sub

【4. 设计Controller】
我们现在分析完了所有单独的信号和他们应该有的值,那么现在可以来设计controller了。
通常电路设计的步骤是:
- 填写
truth table
- input:opcode
- output: 各种控制信号 - 找到每一个信号的简化的表示

Output




Inputs

设计电路
生成一个信号,当这个指令是xxx时,信号为1 ⇒ 使用inverter(01反转器, 图中的圆圈)
电路设计如下:





6.6 指令执行
Instruction Execution指令执行=
- 从一个或多个存储元件(寄存器/内存)中读取内容
- 根据一些组合逻辑完成计算
- 将结果写到一个或多个存储元件中(寄存器/内存)
这些执行过程都在一个时钟周期内:

单一时钟周期的缺点
假设延迟可忽略不计,计算周期时间,可以得到(单位:ns):
【内存操作2ns,ALU/adders 2ns,读取寄存器文件1ns】

如果我们将一整个过程的时长作为时钟周期,我们至少要将周期设为8ns(因为根据“水桶原则”,我们要考虑的是这里面的最短板,也就是用时最长的那个),这就会让每个指令的周期时间很长。
解决方法一:多周期
我们将执行的步骤划分为多个小块,每块的周期都设为2ns:
- 取指令
- 指令解码和寄存器读取
- ALU 运算
- 内存读/写
- 寄存器写入
那么,各指令的时长将变为:

看起来总的时间好像变长了,这就需要用到我们进一步的解决方案。解决方法二:流水线 Pipelining
也就是我们可以同时进行(不同指令的)这几个步骤(1. 取指令 2. 指令解码和寄存器读取 3. ALU 运算 4. 内存读/写 5. 寄存器写入)
详见下一章节。
7. 流水线 Pipelining
引例:洗衣服
分段工作:一个完整的任务完成再下一个。

流水线:每个“资源”被使用完毕后可以被下一个任务所使用。

7.1 Introduction
- 流水线没法解决单个任务的延迟的
latency,但可以提升整体工作的吞吐量 - 使用不同资源的多个任务可以同时进行
- 可能存在的延迟
delays:- pipeline速率会被最慢的那个阶段限制住
- 会为依赖项
dependency停顿
7.2 MIPS Pipeline Stages
- 五个执行阶段
IF, Instruction Fetch:指令获取ID, Instruction Decode and Register Read:指令解码、读取寄存器EX, Execute an operation or calculate an address:执行一个操作或计算一个地址MEM, Access an operand in data memory:访问数据内存中的一个操作数WB, Write back the result into a register:将结果写回寄存器
- Idea
- 每个执行阶段包括一个时钟周期
- 一般的数据流是从一个阶段到下一个阶段
- 例外:程序计数器的更新和写回寄存器(数据流方向相反)

流水线式的执行过程
Pinelined Execution多个指令同时在管道中。

7.3 数据流
MIPS Pineline: Datapath-
单一周期
Single-cycle- 在时钟周期的结尾,更新所有的状态元件(PC、寄存器文件register file、数据内存data memory)
-
流水线式
Pinelined- 流水线的每个阶段是一个时钟周期
- 每一个阶段需要的数据需要被单独存储
-
下一条指令要用到的数据,存储在程序员可以看到的状态元件里(PC、寄存器文件register file、数据内存data memory)
-
同一条指令在下一个pipeline阶段要用到的数据,存储在额外的寄存器例(流水线专用寄存器pinepline registers)
IF/ID:在IF ID之间的寄存器ID/EX:在ID EX之间的寄存器EX/MEM:在EX MEM之间的寄存器MEM/WB:在MEM WB之间的寄存器
图中有颜色的就是pipeline寄存器。

IF Stage

在时钟周期的结束阶段,IF/ID获取(存储):- 从指令内存中读取到的指令,PC+4
- PC+4:也连接到MUX的其中一个输入
ID Stage


EX Stage


MEM Stage


WB Stage


这里有个问题是,此时写回的寄存器号码已经更改了(因为后续的pipeline会覆盖前面的结果)。修正版数据流
Corrected Datapath- 观察“写入寄存器
write register”的号码- IF/ID pipeline寄存器提供的write register已经不是写回阶段要写入的寄存器了。
- 解决方法:
- 将“write register”的号码从 ID/EX阶段传到EX/MEM阶段再传到MEM/WB阶段。也就是说,让write register的号码单独跟随pipeline向下传直到WB阶段需要用到它。

7.4 流水线控制
Pipeline Control- 和单一周期数据流
single-cycle datapath一样的控制信号 - 区别:每个控制信号属于一个特定的pipeline阶段

Pineline Control:Grouping

Pipeline Control: Implementation



7.5 对比不同的实现方式

单一时钟周期处理器的性能
Cycle time :
- C T s e q = ∑ k = 1 N T k CT_{seq} = \sum^N_{k=1} T_k CTseq=∑k=1NTk
- Tk = stage k 需要用到的操作时间
- N = 阶段数
m个指令的执行时间:
- T i m e s e q = C y c l e s ∗ C y c l e T i m e = m ∗ C T s e q = m ∗ ∑ k = 1 N T k Time_{seq} = Cycles * CycleTime = m * CT_{seq} = m * \sum^N_{k=1} T_k Timeseq=Cycles∗CycleTime=m∗CTseq=m∗∑k=1NTk
举例:

CycleTime需要选最长的单个指令执行时间,在例子中就是8ns
执行100条指令所需时间:100 * 8ns = 800ns多个时钟周期处理器的性能
Cycle time :
- C T m u l t i = m a x ( T k ) CT_{multi} = max(T_k) CTmulti=max(Tk)
- m a x ( T k ) = N 个阶段中需要的最多时间 max(T_k) = N个阶段中需要的最多时间 max(Tk)=N个阶段中需要的最多时间
m个指令的执行时间:
- T i m e m u l t i = C y c l e s ∗ C y c l e T i m e = m ∗ A v e r a g e C P I ∗ C T m u l t i Time_{multi} = Cycles * CycleTime = m * Average CPI * CT_{multi} Timemulti=Cycles∗CycleTime=m∗AverageCPI∗CTmulti
- Average CPI: 每个指令需要不同数量的时钟周期去完成
举例,

CycleTime:选择其中最长的阶段时间 = 2ns
执行100条指令,给定average CPI 为4.6: 100 ∗ 4.6 ∗ 2 n s = 920 n s 100 * 4.6 * 2ns = 920ns 100∗4.6∗2ns=920nsPipeline处理器的性能
Cycle time :
-
C
T
p
i
p
e
l
i
n
e
=
m
a
x
(
T
k
)
+
T
d
CT_{pipeline} = max(T_k) + T_d
CTpipeline=max(Tk)+Td
- m a x ( T k ) max(T_k) max(Tk) = N个阶段中最长的阶段时间
-
T
d
T_d
Td = pipeline所需的时间
pipeline overhead
m个指令的执行周期数量:
m + N − 1 m + N - 1 m+N−1 (其中N-1是填满流水线最基本的“浪费”)m个指令的执行时间:
T i m e p i p e l i n e = C y c l e ∗ C T p i p e l i n e = ( m + N − 1 ) ∗ ( m a x ( T k ) + T d ) Time_{pipeline} = Cycle * CT_{pipeline} = (m + N - 1) * (max(T_k) + T_d) Timepipeline=Cycle∗CTpipeline=(m+N−1)∗(max(Tk)+Td)举例:

CycleTime:
假设pipeline register的延迟是0.5ns
longest stage time + overhead = 2 + 0.5 = 2.5 ns执行100条指令所需时间:
( 100 + 5 − 1 ) ∗ 2.5 n s = 260 n s (100 + 5 - 1) * 2.5ns = 260ns (100+5−1)∗2.5ns=260ns理想的性能提升比例 Pipeline Processor: Ideal Speedup
理想化的假设:
- 每个阶段需要同样的时间 : ∑ k = 1 N T k = N ∗ T k \sum_{k=1}^N T_k = N * T_k ∑k=1NTk=N∗Tk
- 没有pipeline overhead : T d = 0 T_d = 0 Td=0
- 待执行指令的数量m远远大于阶段数量N
【这些同样也表明了pipeline processor是在哪些阶段“损失”性能的】
S p e e d u p p i p e l i n e = T i m e s e q / T i m e p i p e l i n e = ( m ∗ ∑ k = 1 N T k ) / ( ( m + N − 1 ) ∗ ( m a x ( T k ) + T d ) ) = ( m ∗ N ∗ T k ) / ( m + N − 1 ) ∗ T k ≈ ( m ∗ N ∗ T k ) / ( m ∗ T k ) ≈ N Speeduppipeline=Timeseq/Timepipeline=(m∗N∑k=1Tk)/((m+N−1)∗(max(Tk)+Td))=(m∗N∗Tk)/(m+N−1)∗Tk≈(m∗N∗Tk)/(m∗Tk)≈N Speeduppipeline=Timeseq/Timepipeline=(m∗k=1∑NTk)/((m+N−1)∗(max(Tk)+Td))=(m∗N∗Tk)/(m+N−1)∗Tk≈(m∗N∗Tk)/(m∗Tk)≈N
总结:
Pipeline processor可以获得N倍的速度提升,其中N是pipeline阶段的数量。
8. Caches
寄存器位于处理器的数据路径中。 如果操作数在内存中,我们必须将它们加载到处理器(寄存器),对它们进行操作,然后将它们存储回内存。

- SRAM:低密度,高访问速度,更贵,多使用
flip-flops电路(触发器) - DRAM:高密度,低访问速度,没那么贵,主要用在主内存中

使用内存技术的层次结构:- CPU附近的小而快的内存
- 远离 CPU 的大而慢的内存
将经常和最近使用的数据保存在更小但更快的内存中,
仅当在更快的内存中找不到数据/指令时,再去更大更慢的内存中查。在很小的时间间隔内,程序只访问一小部分内存地址空间。

时间布局Temporal locality:如果一个项目被引用,它往往会很快再次被引用
空间布局Spatial locality:如果一个项目被引用,附近的项目将很快被引用
不同的布局为指令和数据。
不同的执行阶段可能使用不同的工作集。我们的目标是发现工作集并将其保存在最靠近 CPU 的内存中。如何让 较慢的 主内存显得更快?
缓存——靠近 CPU 的小而快的 SRAM
硬件管理:对程序员透明如何使 较小的 主内存看起来比实际更大?
虚拟内存
操作系统管理:对程序员透明8.2 内存访问时间的术语
Memory Access Time- 命中
Hit:数据在缓存中。- 命中率
Hit rate:命中的内存访问比例 - 命中时间:访问缓存的时间
- 命中率
- 未命中
Miss:数据不在缓存中。- 未命中率 = 1 – 命中率
- 未命中惩罚:替换缓存块的时间+命中时间
- 命中时间 < 未命中惩罚
公式
平均访问时间 = 命中率 x 命中时间 + (1-命中率) x 未命中惩罚
例子:假设我们的片上 SRAM(高速缓存)的访问时间为 0.8 ns,但我们可以获得的最快的 DRAM(主存储器)的访问时间为 10ns。 我们需要多高的命中率才能维持 1ns 的平均访问时间?
Let h be the desired hit rate.
1 = 0.8h + (1 – h) * (10 + 0.8) = 0.8h + 10.8 – 10.8h
10h = 9.8 -> h = 0.98
Hence we need a hit rate of 98%.8.3 内存到缓存映射
Memory to Cache Mapping缓存块/行:内存和缓存之间的传输单位
块大小通常是一个或多个word
例如:16 字节的块 约等于 4 字块;32 字节的块 约等于 8 字块为什么块大小 大于 字大小?



观察:
2N 字节块在 2N 字节边界处对齐
2N 字节块内的字地址具有相同的 (32-N) 最高有效位 (MSB)。
位 [31:N] -> 块号
位 [N-1:0] -> 块内的字节偏移量 -
相关阅读:
lombok 引入
TensorFlow 的基本概念和使用场景
腾讯云/阿里云国际站免费账号:腾讯云国际站如何对象存储cos设置防盗链
easyHttp -- 轻量级的 HTTP 客户端工具包
冷冻电镜聚类中心(2D Class)粒子图像的解析
信用卡评测系列——阳光惠生活APP深化服务客户品牌理念,焕新升级7.0版
EI/知网检索高录用国际学术会议推荐
Vue3二维码生成(简洁明了)
【软考软件评测师】第十七章 计算机组成与体系结构(总线技术)
音视频会议需要哪些设备配置
- 原文地址:https://blog.csdn.net/CherryChenieth/article/details/126676007
