🚀 优质资源分享 🚀

论文信息

论文标题：PairNorm: Tackling Oversmoothing in GNNs论文作者：Lingxiao Zhao, Leman Akoglu论文来源：2020,ICLR论文地址：download 论文代码：download

1 Introduction

GNNs 的表现随着层数的增加而有所下降，一定程度上归结于 over-smoothing 问题，重复图卷积操作会使得节点表示最终变得不可区分。为缓解过平滑问题提出了 PairNorm， 一种归一化方法。

比较可惜的时，该论文在使用了 2022 年的 “Mask” 策略，可惜了实验做的不咋好。为什么失败，见文末。太可惜了…

2 Understanding oversmoothing

Definition

˜Asym=˜D−1/2˜A˜D−1/2A_sym=D−1/2A_D−1/2\tilde{\mathbf{A}}_{\mathrm{sym}}=\tilde{\mathbf{D}}^{-1 / 2} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-1 / 2}

˜Arw=˜D−1˜AA_rw=D−1A~\tilde{\mathbf{A}}_{\mathrm{rw}}=\tilde{\mathbf{D}}^{-1} \tilde{\mathbf{A}}

2.1 The oversmoothing problem

2.1.1 Oversmoothing

GNN 性能下降的原因：

• • 参数数量的增加；
    • 梯度消失导致训练困难；
    • 图卷积而造成的过平滑；

过平滑的考虑方法如下：当多次使用拉普拉斯平滑导致节点特征收敛到一个平稳点。假设 x⋅j∈Rn\mathbf{x}_{\cdot j} \in \mathbb{R}^{n} 表示 X\mathbf{X} 的第 jj 列，对于任意 x⋅j∈Rn\mathbf{x}_{\cdot j} \in \mathbb{R}^{n}：

limk→∞˜Aksymx⋅j=πj and πj‖πj‖1=π

其中，标准化解 π∈Rn\pi \in \mathbb{R}^{n} 满足 πi=√degi∑i√degi for all i∈[n]\boldsymbol{\pi}_{i}=\frac{\sqrt{\operatorname{deg}_{i}}}{\sum_{i} \sqrt{\operatorname{deg}_{i}}}  \text{ for all }  i \in[n]。

Note：π\boldsymbol{\pi} 不依赖于节点特征矩阵，而是一个单纯依靠图结构度的函数。

2.1.2 Its Measurement

本文提出两种度量过平滑的方式：row-diff\text{row-diff} 和  col-diff\text{col-diff}。

设 H(k)∈Rn×d\mathbf{H}^{(k)} \in \mathbb{R}^{n \times d} 为第 kk 个图卷积后的节点表示矩阵，即 H(k)=˜AksymX\mathbf{H}^{{(k)}=\tilde{\mathbf{A}}_{\mathrm{sym}}}{k} \mathbf{X}。设 h(k)i∈Rd\mathbf{h}_{i}^{(k)} \in \mathbb{R}^{d} 为 H(k)\mathbf{H}^{(k)} 的第 ii 行，h(k).i∈Rn\mathbf{h}_{. i}^{(k)} \in \mathbb{R}^{n} 为 H(k)\mathbf{H}^{(k)} 的第 ii 列。

row-diff(H(k))\text{row-diff}(  \left.\mathbf{H}^{(k)}\right) 和 col-diff(H(k))\text{col-diff}(  \left.\mathbf{H}^{(k)}\right) 的定义如下：

row−diff(H(k))=1n2∑i,j∈[n]‖h(k)i−h(k)j‖2(2){\large \operatorname{row}-\operatorname{diff}\left(\mathbf{H}^{(k)}\right) =\frac{1}{n^{2}} \sum\limits _{i, j \in[n]}\left|\mathbf{h}_{i}^{{(k)}-\mathbf{h}_{j}}{(k)}\right|_{2}}  \quad\quad\quad(2)

col-diff(H(k))=1d2∑i,j∈[d]‖h(k)⋅i‖h(k)⋅i‖1−h(k)⋅j‖h(k)⋅j‖1‖2(3){\large \operatorname{col-diff}\left(\mathbf{H}^{(k)}\right) =\frac{1}{d^{2}} \sum\limits _{i, j \in[d]}|    \frac{\mathbf{h}_{\cdot i}^{(k)}}{|\mathbf{h}_{\cdot i}^{(k)}|_{1}}-\frac{\mathbf{h}_{\cdot j}^{(k)}}{|\mathbf{h}_{\cdot j}^{(k)}|_{1}}   |_{2}} \quad\quad\quad(3)
　　row-diff\text{row-diff} 量化节点之间的成对距离，而 col-diff\text{col-diff} 特征之间的成对距离。

2.2 Studying oversmoothing with SGC

GCN 过平滑可能由于层数增加导致的性能下降，即添加更多的层导致更多的参数（添加的线性层 存在 W(k)\mathbf{W}^{(k)}）容易导致过拟合。同样层数增加，容易存在反向传播梯度的消失（应该指的是参数多）。

将层数增加影响过平滑和 使用参数导致过拟合即反向传播梯度消失 解耦。本文使用 SGC ，一种简化的 GCN :去除图卷积层的所有投影参数和所有层间的非线性激活。SGC可写为：

ˆY=softmax(˜AKsymXW)(4)\widehat{\boldsymbol{Y}}=\operatorname{softmax}\left(\tilde{\mathbf{A}}_{\mathrm{sym}}^{K} \mathbf{X} \mathbf{W}\right) \quad\quad\quad(4)

其中，KK 为图卷积的个数，W∈Rd×c\mathbf{W} \in \mathbb{R}^{d \times c} 表示可学习参数。
　　Note：SGC有一个固定数量的参数，不依赖于图卷积的数量（即层），也因此防止了过拟合和消失梯度问题的影响。

那么，这只给我们留下了过平滑作为随着 KK 增加的性能下降的可能原因。需要注意的是 SGC 并不是一种牺牲，在某些分类任务似乎有更好或者相似的准确性。
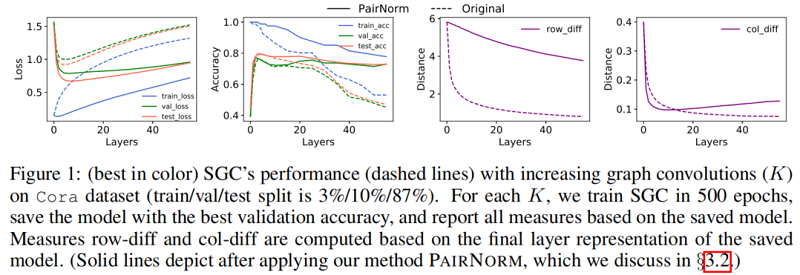
　　Figure 1 中的虚线说明了当增加层数( KK )时，SGC 在 Cora 数据集上的性能。训练（交叉熵）损失随着 KK 的增大而单调地增加，这可能是因为图卷积将节点表示与它们的邻居混合在一起，使它们变得不那么容易区分（训练变得更加困难）。另一方面，至多到 K=4K=4，图卷积（即平滑）提高了泛化能力，减少了训练和验证/测试损失之间的差距，之后，过平滑开始影响性能。row-diff\text{row-diff} 和 col-diff\text{col-diff} 都随 KK 继续单调递减，为过平滑提供了支持证据。

3 Tackling oversmoothing

3.1 Proposed pairnorm

考虑图正则化最小二乘(GRLS)：设 ¯X∈Rn×d\overline{\mathbf{X}} \in \mathbb{R}^{n \times d} 是节点表示矩阵，其中 ¯xi∈Rd\overline{\mathbf{x}}_{i} \in \mathbb{R}^{d} 表示 ¯X\overline{\mathbf{X}} 的第 ii 行，GRLS 问题为：

min¯x∑i∈V‖¯xi−xi‖2˜D+∑(i,j)∈E‖¯xi−¯xj‖22(5)\underset{\overline{\mathbf{x}}}{\text{min}} \sum\limits _{i \in \mathcal{V}}\left|\overline{\mathbf{x}}_{i}-\mathbf{x}_{i}\right|_{\tilde{\mathbf{D}}}^{2}+\sum\limits_{(i, j) \in \mathcal{E}}\left|\overline{\mathbf{x}}_{i}-\overline{\mathbf{x}}_{j}\right|_{2}^{2}\quad\quad\quad(5)

其中：

• • ‖zi‖2˜D=zTi˜Dzi\left|\mathbf{z}_{i}\right|_{\tilde{\mathbf{D}}}^{{2}=\mathbf{z}_{i}}{T} \tilde{\mathbf{D}} \mathbf{z}_{i}；

第一项可以看作是度加权最小二乘，第二个是一个图正则化项，度量新特征在图结构上的变化。

优化问题的目标可认为是估计新的 “去噪” 特征 ¯xi\overline{\mathbf{x}}_{i} 离输入特征 xi\mathbf{x}_{i} 不远，并且在图结构上很平滑。

GRLS 问题有一个封闭形式的解 ¯X=(2I−˜Arw)−1X\overline{\mathbf{X}}=\left(2 \mathbf{I}-\tilde{\mathbf{A}}_{\mathrm{rw}}\right)^{-1} \mathbf{X}，其中 ˜ArwX\tilde{\mathbf{A}}_{\mathrm{rw}} \mathbf{X} 是一阶泰勒近似，即 ˜ArwX≈¯X\tilde{\mathbf{A}}_{\mathrm{rw}} \mathbf{X} \approx \overline{\mathbf{X}}。通过替换 ˜Arw\tilde{\mathbf{A}}_{\mathrm{rw}} 为 ˜Asym \tilde{\mathbf{A}}_{\text {sym }}，得到与图卷积相同的形式，即 ˜X=˜Asym X≈¯X\tilde{\mathbf{X}}=\tilde{\mathbf{A}}_{\text {sym }} \mathbf{X} \approx \overline{\mathbf{X}}。因此，图卷积可以看作是 Eq.5\text{Eq.5} 的近似解，它最小化了图结构上的变化，同时保持新的表示接近原始表示。
　　理想情况下，希望获得对同一集群内的节点的平滑，但是避免平滑来自不同集群的节点。Eq.5\text{Eq.5} 中的目标通过图正则化项只优化第一个目标。因此，当重复应用卷积时，它容易出现过平滑。为规避这个问题并同时实现这两个目标，可以添加一个负项，如没有边连接对之间的距离之和如下：

min¯x∑i∈V‖¯xi−xi‖2˜D+∑(i,j)∈E‖¯xi−¯xj‖22−λ∑(i,j)∉E‖¯xi−¯xj‖22(6)\underset{\overline{\mathbf{x}}}{\text{min}}  \sum\limits _{i \in \mathcal{V}}\left|\overline{\mathbf{x}}_{i}-\mathbf{x}_{i}\right|_{\tilde{\mathbf{D}}}^{2}+\sum\limits_{(i, j) \in \mathcal{E}}\left|\overline{\mathbf{x}}_{i}-\overline{\mathbf{x}}_{j}\right|_{2}^{2}-\lambda \sum_{(i, j) \notin \mathcal{E}}\left|\overline{\mathbf{x}}_{i}-\overline{\mathbf{x}}_{j}\right|_{2}^{2}\quad\quad\quad(6)

同样，可通过推导 Eq.6\text{Eq.6} 的封闭型解并用一阶泰勒展开进行逼近，得到一个具有超参数 λ\lambda 的修正图卷积算子。
　　在本文中，没有提出了一个全新的图卷积算子，而是提出了一个通用的、有效的 “补丁”，称为 PAIRNORM，它可以应用于具有过平滑潜力的任何形式的图卷积。

设 ˜X\tilde{\mathbf{X}}（图卷积的输出）和 ˙X\dot{\mathbf{X}} 分别为 PAIRNORM 的输入和输出。观察到图卷积 ˜X=˜Asym X\tilde{\mathbf{X}}=\tilde{\mathbf{A}}_{\text {sym }} \mathbf{X} 的输出实现了第一个目标 度加权，PAIRNORM 作为一个标准化层，在 ˜X\tilde{\mathbf{X}} 上工作，以实现第二个目标，即保持未连接的对表示更远。具体来说，PAIRNORM 将 ˜X\tilde{\mathbf{X}} 归一化，使总成对平方距离 TPSD(˙X):=∑i,j∈[n]‖˙xi−˙xj‖22\operatorname{TPSD}(\dot{\mathbf{X}}):=\sum\limits_{i, j \in[n]}\left|\dot{\mathbf{x}}_{i}-\dot{\mathbf{x}}_{j}\right|_{2}^{2} 和 TPSD(X)\operatorname{TPSD}(\mathbf{X} ) 一样：

∑(i,j)∈E‖˙xi−˙xj‖22+∑(i,j)∉E‖˙xi−˙xj‖22=∑(i,j)∈E‖xi−xj‖22+∑(i,j)∉E‖xi−xj‖22(7) \sum\limits_{(i, j) \in \mathcal{E}}\left|\dot{\mathbf{x}}_{i}-\dot{\mathbf{x}}_{j}\right|_{2}^{2}+\sum\limits_{(i, j) \notin \mathcal{E}}\left|\dot{\mathbf{x}}_{i}-\dot{\mathbf{x}}_{j}\right|_{2}^{2}=\sum\limits_{(i, j) \in \mathcal{E}}\left|\mathbf{x}_{i}-\mathbf{x}_{j}\right|_{2}^{2}+\sum\limits_{(i, j) \notin \mathcal{E}}\left|\mathbf{x}_{i}-\mathbf{x}_{j}\right|_{2}^{2} \quad\quad\quad(7)
　　理想情况下，希望 ∑(i,j)∉E‖˙xi−˙xj‖22\sum\limits _{(i, j) \notin \mathcal{E}}\left|\dot{\mathbf{x}}_{i}-\dot{\mathbf{x}}_{j}\right|_{2}^{2} 和 ∑(i,j)∉E‖xi−xj‖22\sum\limits _{(i, j) \notin \mathcal{E}}\left|\mathbf{x}_{i}-\mathbf{x}_{j}\right|_{2}^{2} 一样大，∑(i,j)∈E‖˙xi−˙xj‖22≈∑(i,j)∈E‖˜xi−˜xj‖22\sum\limits _{(i, j) \in \mathcal{E}}\left|\dot{\mathbf{x}}_{i}-\dot{\mathbf{x}}_{j}\right|_{2}^{2} \approx \sum\limits _{(i, j) \in \mathcal{E}}\left|\tilde{\mathbf{x}}_{i}-\tilde{\mathbf{x}}_{j}\right|_{2}^{2} 是由于拉普拉斯平滑的原因。
　　实践中，不需要时刻关注 TPSD(X)\operatorname{TPSD}(\mathbf{X} ) 的值，只需要在所有层使得 TPSD(X)\operatorname{TPSD}(\mathbf{X} ) 保持一个恒定的常量 CC。

为计算 TPSD(X)\operatorname{TPSD}(\mathbf{X} ) 的常数值，可先计算 TPSD(˜X)\operatorname{TPSD}(\tilde{\mathbf{X}})。当然直接计算 TPSD(˜X)\operatorname{TPSD}(\tilde{\mathbf{X}}) 涉及到 n2n^{2} 个成对的距离 O(n2d)\mathcal{O}\left(n^{2} d\right)，这对大数据集来说是十分耗时间的。

同样地，规范化可以通过一个两步的方法来完成，其中  TPSD\operatorname{TPSD} 被重写为

TPSD(˜X)=∑i,j∈[n]‖˜xi−˜xj‖22=2n2(1nn∑i=1‖˜xi‖22−‖1nn∑i=1˜xi‖22)(8)\operatorname{TPSD}(\tilde{\mathbf{X}})=\sum\limits_{i, j \in[n]}\left|\tilde{\mathbf{x}}_{i}-\tilde{\mathbf{x}}_{j}\right|_{2}^{2}=2 n^{2}\left(\frac{1}{n} \sum\limits_{i=1}^{{n}\left|\tilde{\mathbf{x}}_{i}\right|_{2}}{2}-\left|\frac{1}{n} \sum\limits_{i=1}^{n} \tilde{\mathbf{x}}_{i}\right|_{2}^{2}\right) \quad\quad\quad(8)

Eq.8\text{Eq.8} 的第一项 表示节点表示的均方长度，第二项描述了节点表示的均值的平方长度。

为简化 Eq.8\text{Eq.8} 的计算，令每个 ˜xi\tilde{\mathbf{x}}_{i} 减去行均值 ˜xci=˜xi−1nn∑i˜xi\tilde{\mathbf{x}}_{i}^{c}=\tilde{\mathbf{x}}_{i}-\frac{1}{n} \sum\limits _{i}^{n} \tilde{\mathbf{x}}_{i}，其中 ˜xci\tilde{\mathbf{x}}_{i}^{c} 表示中心表示。这种移动不会影响 TPSD\operatorname{TPSD}，并且驱动了项 ‖1nn∑i=1˜xi‖22\left|\frac{1}{n} \sum\limits _{i=1}^{n} \tilde{\mathbf{x}}_{i}\right|_{2}^{2} 趋近 00。那么，计算 TPSD(˜X)\operatorname{TPSD}(\tilde{\mathbf{X}}) 可归结为计算 ˜Xc\tilde{\mathbf{X}}^{c} 的 FF 范数的平方，并有 O(nd)\mathcal{O}(n d)：

TPSD(˜X)=TPSD(˜Xc)=2n‖˜Xc‖2F(9)\operatorname{TPSD}(\tilde{\mathbf{X}})=\operatorname{TPSD}\left(\tilde{\mathbf{X}}^{c}\right)=2 n\left|\tilde{\mathbf{X}}^{{c}\right|_{F}}{2} \quad\quad\quad(9)

Eq.9\text{Eq.9} 可以写成一个两步的、中心和规模的归一化过程：

˜xci=˜xi−1nn∑i=1˜xi(Center)(10)\tilde{\mathbf{x}}_{i}^{c}=\tilde{\mathbf{x}}_{i}-\frac{1}{n} \sum\limits _{i=1}^{n} \tilde{\mathbf{x}}_{i}  \quad\quad\text{(Center)}\quad(10)

˙xi=s⋅˜xci√1nn∑i=1‖˜xci‖22=s√n⋅˜xci√‖˜Xc‖2F(Scale)(11)\dot{\mathbf{x}}_{i}=s \cdot \frac{\tilde{\mathbf{x}}_{i}^{c}}{\sqrt{\frac{1}{n} \sum\limits_{i=1}^{{n}\left|\tilde{\mathbf{x}}_{i}}{c}\right|_{2}^{2}}}=s \sqrt{n} \cdot \frac{\tilde{\mathbf{x}}_{i}^{{c}}{\sqrt{\left|\tilde{\mathbf{X}}}{c}\right|_{F}^{2}}} \quad\quad\text{(Scale)}\quad(11)
　　缩放后，数据保持中心化 ‖n∑i=1˙xi‖22=0\left|\sum\limits _{i=1}^{n} \dot{\mathbf{x}}_{i}\right|_{2}^{2}=0 。在 Eq.11\text{Eq.11} 中，ss 是一个超参数，它决定了 CC。具体来说，

TPSD(˙X)=2n‖˙X‖2F=2n∑i‖s⋅˜xci√1n∑i‖˜xci‖22‖22=2ns21n∑i‖˜xci‖22∑i‖˜xci‖22=2n2s2(12)\operatorname{TPSD}(\dot{\mathbf{X}})=2 n|\dot{\mathbf{X}}|_{F}^{2}=2 n \sum\limits_{i}\left|s \cdot \frac{\tilde{\mathbf{x}}_{i}^{c}}{\sqrt{\frac{1}{n} \sum\limits_{i}\left|\tilde{\mathbf{x}}_{i}^{{c}\right|_{2}}{2}}}\right|_{2}^{2}=2 n \frac{s^{2}}{\frac{1}{n} \sum\limits_{i}\left|\tilde{\mathbf{x}}_{i}^{{c}\right|_{2}}{2}} \sum\limits_{i}\left|\tilde{\mathbf{x}}_{i}^{{c}\right|_{2}}{2}=2 n^{2} s^{2} \quad(12)

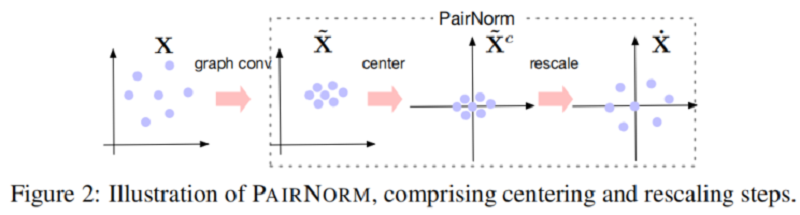
然后，˙X:=PAIRNORM(˜X)\dot{\mathbf{X}}:=\operatorname{PAIRNORM}(\tilde{\mathbf{X}}) 拥有行均值为 00 （Center），和恒定的总成对平方距离 C=2n2s2C=2 n^{2} s^{2}。在 Figure 2 中给出了一对范数的说明。PAIRNORM 的输出被输入到下一个卷积层。

本文还推导出 PAIRNORM 的变体，即通过替换 Eq.11\text{Eq.11} 的 n∑i=1‖˜xci‖22\sum\limits _{i=1}^{{n}\left|\tilde{\mathbf{x}}_{i}}{c}\right|_{2}^{2}  为 n‖˜xci‖22n\left|\tilde{\mathbf{x}}_{i}^{{c}\right|_{2}}{2} ，本文称之为 PAIRNORM-SI ，此时所有的节点都有相同的 L2L_{2} 范数 ss 。

在实践中，发现 PAIRNORM 和 PAIRNORM-SI 对 SGC 都很有效，而 PAIRNORM-SI 对 GCN 和 GAT 提供了更好和更稳定的结果。GCN 和 GAT 需要更严格的归一化的原因可能是因为它们有更多的参数，更容易发生过拟合。在所有实验中，对SGC采用PAIRNORM，对 GCN 和 GAT 采用 PAIRNORM-SI。

Figure 1 中的实线显示了 SGC 性能， 与 “vanilla” 版本相比，随着层数的增加，我们在每个图卷积层之后使用 PAIRNORM。类似地，Figure 3 用于 GCN 和 GAT（在每个图卷积激活后应用PAIRNORM-SI）。请注意，PAIRNORM 的性能衰减要慢得多。

虽然 PAIRNORM 使更深层次的模型对过度平滑更稳健，但总体测试精度没有提高似乎很奇怪。事实上，文献中经常使用的基准图数据集需要不超过 44 层，之后性能就会下降（即使是缓慢的）。

3.2 A case where deeper GNNs are beneficial

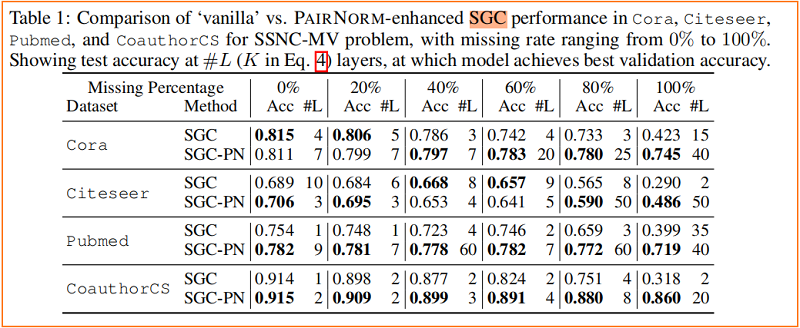
如果一个任务需要大量的层来实现其最佳性能，那么它将更多的收益于使用 PAIRNORM，为此本文研究了 “missing feature setting”，即节点的一个子集存在特征缺失。
　　假设 M⊆Vu\mathcal{M} \subseteq \mathcal{V}_{u} 代表特征缺失子集，其中 ∀m∈M\forall m \in \mathcal{M}，xm=∅\mathbf{x}_{m}=\emptyset 。本文设置 p=|M|/|Vu|p=|\mathcal{M}| /\left|\mathcal{V}_{u}\right| 代表缺失比例。将这种任务的变体称为具有缺失向量的半监督节点分类(SSNC-MV)。直观的说，需要更多的传播步骤才能恢复这些节点有效的特征表示。

Figure 4 显示了随着层数的增加，SGC、GCN 和 GAT 模型在 Cora 上的性能变化，其中我们从所有未标记的节点中删除特征向量，即 p=1p=1。与没有PAIRNORM 的模型相比，具有 PAIRNORM 的模型获得了更高的测试精度，它们通常会达到更多的层数。

4 Experiments

在本节中，我们设计了广泛的实验来评估在SSNC-MV设置下的SGC、GCN和GAT模型的有效性。

4.1 Experiment setup

4.2 Experiment results

核心代码：

if \_\_name\_\_ == "\_\_main\_\_":
    mode = 'PN'
    scale = 1
    x  =torch.randint(0,10,(3,2)).type(torch.float)
    col\_mean = x.mean(dim=0)
    if mode == 'PN':
        x = x - col\_mean
        print("x = ",x)
        rownorm\_mean = (1e-6 + x.pow(2).sum(dim=1).mean()).sqrt()
        x = scale * x / rownorm\_mean

    if mode == 'PN-SI':
        x = x - col\_mean
        rownorm\_individual = (1e-6 + x.pow(2).sum(dim=1, keepdim=True)).sqrt()
        x = scale * x / rownorm\_individual

    if mode == 'PN-SCS':
        rownorm\_individual = (1e-6 + x.pow(2).sum(dim=1, keepdim=True)).sqrt()
        x = scale * x / rownorm\_individual - col\_mean
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

节点分类

代码以 Deep_GCN 为例子：

class DeepGCN(nn.Module):
    def \_\_init\_\_(self, nfeat, nhid, nclass, dropout, nlayer=2, residual=0,
 norm\_mode='None', norm\_scale=1, **kwargs):
        super(DeepGCN, self).\_\_init\_\_()
        assert nlayer >= 1 
        self.hidden\_layers = nn.ModuleList([
            GraphConv(nfeat if i==0 else nhid, nhid)  for i in range(nlayer-1)
        ])
        self.out\_layer = GraphConv(nfeat if nlayer==1 else nhid , nclass)

        self.dropout = nn.Dropout(p=dropout)
        self.dropout\_rate = dropout
        self.relu = nn.ReLU(True)
        self.norm = PairNorm(norm\_mode, norm\_scale)
        self.skip = residual

    def forward(self, x, adj):
        x\_old = 0
        for i, layer in enumerate(self.hidden\_layers):
            x = self.dropout(x)
            x = layer(x, adj)
            x = self.norm(x)
            x = self.relu(x)
            if self.skip>0 and i%self.skip==0:
                x = x + x\_old
                x\_old = x
            
        x = self.dropout(x)
        x = self.out\_layer(x, adj)
        return x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

5 Conclusion

提出了一种有效防止过平滑问题的 成对范数 ，一种新的归一化层，提高了深度 GNNs 对过平滑的鲁棒性。

6 Reason of failure

即实验对于 mask feature 只处理了一次，并没有在每个 epoch 中进行处理。

def load\_data(data\_name='Cora', normalize\_feature=True, missing\_rate=0, cuda=False):
    # can use other dataset, some doesn't have mask
    print(os.path.join(DATA\_ROOT, data\_name))
    dataset = geo\_data.Planetoid(DATA\_ROOT, data\_name)
    print("dataset = ",dataset)
    # print(dataset[0])
    # print(dataset.data)
    data = geo\_data.Planetoid(DATA\_ROOT, data\_name).data

    # original split
    data.train\_mask = data.train\_mask.type(torch.bool)
    data.val\_mask = data.val\_mask.type(torch.bool)
    # data.test\_mask = data.test\_mask.type(torch.bool) 
    # expand test\_mask to all rest nodes 
    data.test\_mask = ~(data.train\_mask + data.val\_mask)
    # get adjacency matrix
    n = len(data.x)
    adj = sp.csr\_matrix((np.ones(data.edge\_index.shape[1]), data.edge\_index), shape=(n,n))
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj) + sp.eye(adj.shape[0])
    adj = normalize\_adj\_row(adj) # symmetric normalization works bad, but why? Test more. 
    data.adj = to\_torch\_sparse(adj)
    # normalize feature
    if normalize\_feature:
        data.x = row\_l1\_normalize(data.x)
    
    # generate missing feature setting 
    indices\_dir = os.path.join(DATA\_ROOT, data\_name, 'indices')
    if not os.path.isdir(indices\_dir): 
        os.mkdir(indices\_dir)
    missing\_indices\_file = os.path.join(indices\_dir, "indices\_missing\_rate={}.npy".format(missing\_rate))
    if not os.path.exists(missing\_indices\_file):
        erasing\_pool = torch.arange(n)[~data.train\_mask] # keep training set always full feature
        size = int(len(erasing\_pool) * (missing\_rate/100))
        idx\_erased = np.random.choice(erasing\_pool, size=size, replace=False)
        np.save(missing\_indices\_file, idx\_erased)
    else:
        idx\_erased = np.load(missing\_indices\_file)
    # erasing feature for random missing 
    if missing\_rate > 0:
        data.x[idx\_erased] = 0
    
    if cuda:
        data.x = data.x.cuda()
        data.y = data.y.cuda()
        data.adj = data.adj.cuda()
    
    return data 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

View Code

• 论文信息

• 1 Introduction

• 2 Understanding oversmoothing

• 2.1 The oversmoothing problem

• 2.1.1 Oversmoothing

• 2.1.2 Its Measurement

• 2.2 Studying oversmoothing with SGC

• 3 Tackling oversmoothing

• 3.1 Proposed pairnorm

• 3.2 A case where deeper GNNs are beneficial

• 4 Experiments

• 4.1 Experiment setup

• 4.2 Experiment results

• 5 Conclusion

• 6 Reason of failure

  __EOF__

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2G5guV2g-1661101717308)(https://blog.csdn.net/BlairGrowing)]Blair - 本文链接： https://blog.csdn.net/BlairGrowing/p/16607263.html

• 关于博主： 评论和私信会在第一时间回复。或者直接私信我。
• 版权声明： 本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
• 声援博主： 如果您觉得文章对您有帮助，可以点击文章右下角**【[推荐](javascript:void(0)😉】**一下。