信号包络提取的方法

        此示例说明如何提取信号的包络。创建双边带幅值调制信号。载波频率为 1 kHz。调制频率为 50 Hz。调制深度为 100%。采样率为 10 kHz。

t = 0:1e-4:0.1;
x = (1+cos(2*pi*50*t)).*cos(2*pi*1000*t);
 
plot(t,x)
xlim([0 0.04])

        如图所示：

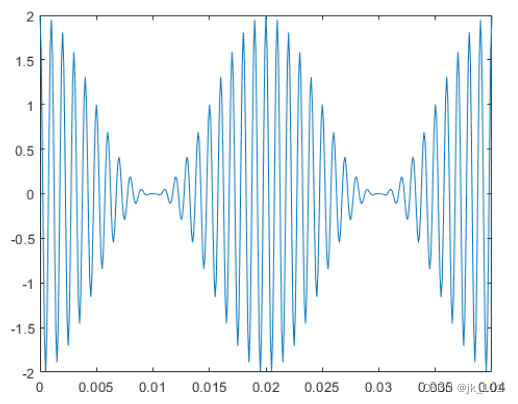
        使用 hilbert 函数提取包络。包络是由 hilbert 计算的解析信号的幅值。绘制包络和原始信号。将 plot 函数的名称-值对组参数存储在元胞数组中，供以后使用。分析信号的幅值捕获信号的缓慢变化特性，而相位包含高频信息。

y = hilbert(x);
env = abs(y);
plot_param = {'Color', [0.6 0.1 0.2],'Linewidth',2}; 
 
plot(t,x)
hold on
plot(t,[-1;1]*env,plot_param{:})
hold off
xlim([0 0.04])
title('Hilbert Envelope')

        如图所示：

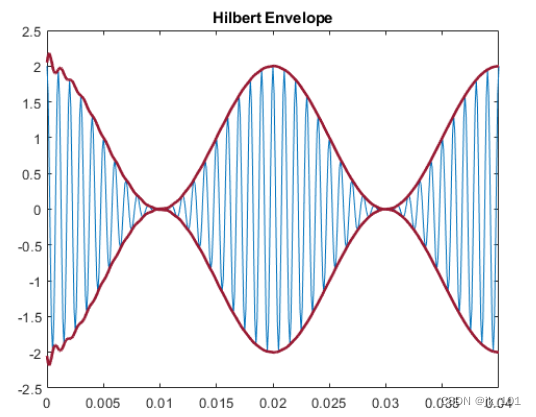
        还可以使用 envelope 函数直接生成信号包络并修改其计算方式。例如，可以调整用于求得分析包络的 Hilbert 滤波器的长度。使用太小的滤波器长度会导致包络失真。 

fl1 = 12;
[up1,lo1] = envelope(x,fl1,'analytic');
fl2 = 30;
[up2,lo2] = envelope(x,fl2,'analytic');
param_small = {'Color',[0.9 0.4 0.1],'Linewidth',2};
param_large = {'Color',[0 0.4 0],'Linewidth',2};
 
plot(t,x)
hold on
p1 = plot(t,up1,param_small{:});
plot(t,lo1,param_small{:});
p2 = plot(t,up2,param_large{:});
plot(t,lo2,param_large{:});
hold off
 
legend([p1 p2],'fl = 12','fl = 30')
xlim([0 0.04])
title('Analytic Envelope')

        如图所示：

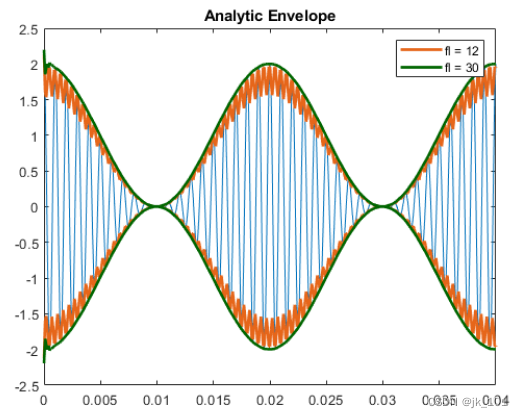
        可以使用滑动窗生成移动 RMS 包络。使用太小的窗长度会导致包络失真。使用太大的窗长度则会平滑掉包络。

wl1 = 3;
[up1,lo1] = envelope(x,wl1,'rms');
wl2 = 5;
[up2,lo2] = envelope(x,wl2,'rms');
wl3 = 300;
[up3,lo3] = envelope(x,wl3,'rms');
 
plot(t,x)
hold on
p1 = plot(t,up1,param_small{:});
plot(t,lo1,param_small{:});
p2 = plot(t,up2,plot_param{:});
plot(t,lo2,plot_param{:});
p3 = plot(t,up3,param_large{:});
plot(t,lo3,param_large{:})
hold off
 
legend([p1 p2 p3],'wl = 3','wl = 5','wl = 300')
xlim([0 0.04])
title('RMS Envelope')

        如图所示：

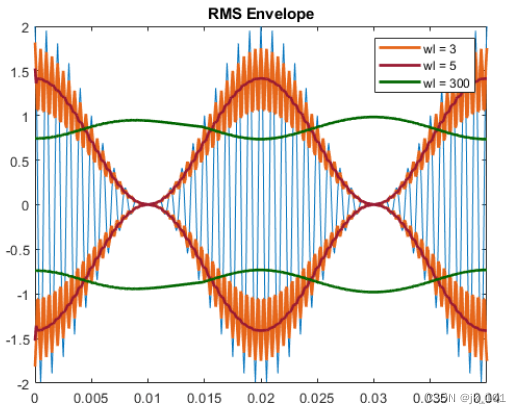
        可以通过对相隔可变数量采样点的局部最大值进行样条插值来生成峰值包络。样本太分散会平滑包络。 

np1 = 5;
[up1,lo1] = envelope(x,np1,'peak');
np2 = 50;
[up2,lo2] = envelope(x,np2,'peak');
 
plot(t,x)
hold on
p1 = plot(t,up1,param_small{:});
plot(t,lo1,param_small{:})
p2 = plot(t,up2,param_large{:});
plot(t,lo2,param_large{:})
hold off
 
legend([p1 p2],'np = 5','np = 50')
xlim([0 0.04])
title('Peak Envelope')

        如图所示：

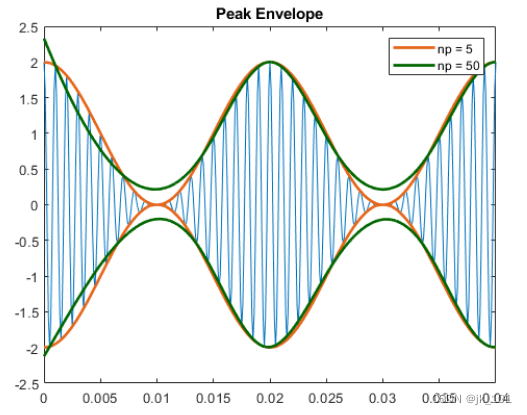
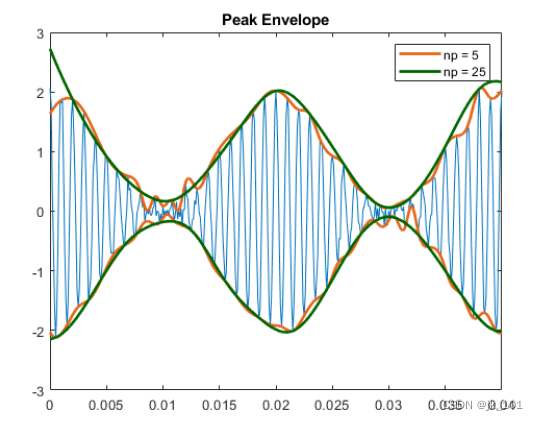
        增大峰值分隔参数可以降低噪声引起的伪峰效应。向信号引入随机噪声。先使用包含 5 个样本的区间了解噪声对峰值包络的影响，然后用包含 25 个样本的区间重新生成峰值包络。 

rng default
q = x + randn(size(x))/10;
np1 = 5;
[up1,lo1] = envelope(q,np1,'peak');
np2 = 25;
[up2,lo2] = envelope(q,np2,'peak');
 
plot(t,q)
hold on
p1 = plot(t,up1,param_small{:});
plot(t,lo1,param_small{:})
p2 = plot(t,up2,param_large{:});
plot(t,lo2,param_large{:})
hold off
 
legend([p1 p2],'np = 5','np = 25')
xlim([0 0.04])
title('Peak Envelope')

        如图所示：