-
矩阵分析与应用(22)
学习来源:《矩阵分析与应用》 张贤达 清华大学出版社
矩阵分析与应用学习小结
一、向量的范数
1. 定义
向量的范数是用来刻画向量大小的一种度量。设映射
 满足:
满足:① 非负性:
,当且仅当
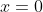 时,
时,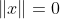 ;
;② 其次性:
 ;
;③ 三角不等式:
 。
。则称映射
 为
为  上向量
上向量 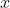 的范数。
的范数。2. 向量的 1 范数
向量的 1 范数是指向量中所有元素的绝对值之和,用公式表示为

其中
![x=[x_1,x_2,\cdots ,x_n]](https://1000bd.com/contentImg/2022/08/14/112154642.gif)
例:
![a=[1,-3,4,7]](https://1000bd.com/contentImg/2022/08/14/112155735.gif)
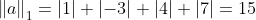
3.向量的 2 范数
向量的 2 范数又称欧几里得范数,表示通常意义上的模,用公式表示为
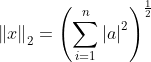
其中,
![x=[x_1,x_2,\cdots ,x_n]](https://1000bd.com/contentImg/2022/08/14/112154642.gif) 。
。例:
![b=[1+i,4i,2\sqrt{2}-i,-2\sqrt{2}]](https://1000bd.com/contentImg/2022/08/14/112203109.gif)

二、矩阵的范数
1. 定义
由于一个
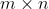 矩阵可以看做
矩阵可以看做  维向量,因此可以按照定义向量范数的方式定义矩阵范数。
维向量,因此可以按照定义向量范数的方式定义矩阵范数。设
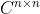 表示复数域
表示复数域  上全体
上全体 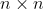 矩阵构成的线性空间,设函数
矩阵构成的线性空间,设函数  满足:
满足:① 非负性:
 ,当且仅当
,当且仅当  时,
时, ;
;② 齐次性:
 ;
;③ 三角不等式:
 ;
;④ 相容性:
 。
。则称
 为矩阵
为矩阵  的范数。
的范数。2. 矩阵的 1 范数
矩阵的 1 范数是矩阵的每一列上的元素绝对值先求和,再从中取最大值(列和最大)。用公式表示为:

其中,
 。
。3. 矩阵的 2 范数
矩阵的 2 范数是矩阵
 的最大特征值开平方,用公式表示为:
的最大特征值开平方,用公式表示为:
其中,
 ,
,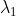 为
为  的最大特征值。
的最大特征值。4. 矩阵的 F 范数
矩阵的 F 范数是矩阵的所有元素的平方和开根号,用公式表示为:

其中,
 。
。5. 矩阵的无穷范数
矩阵的无穷范数是矩阵的每一行上的元素绝对值先求和,再从中取最大值(行和最大)。用公式表示为:

其中,
 。
。6. 例
1)矩阵




2)矩阵


-
相关阅读:
计算机毕业设计Java教师教学质量评估系统(源码+系统+mysql数据库+lw文档)
一个性能强到爆的RPC框架-gRPC
Mybatis plus中的逻辑删除源码跟踪
Mybatics-连接配置
Three.js柏林噪音 流动球体
Unity引擎游戏优化插件MeshSimplify使用说明
java计算机毕业设计夕阳红养老院系统源码+系统+数据库+lw文档+mybatis+运行部署
关于生产企业原材料的订购与运输问题
聊聊ip与mac地址之间那些事
这次彻底搞定CSS层叠、优先级!
- 原文地址:https://blog.csdn.net/qq_40206924/article/details/126272681