​

活动地址：CSDN21天学习挑战赛

二分查找

        二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法，可以在数据规模的对数时间复杂度内完成查找。是一种在有序数组中查找某一特定元素的搜索算法。

算法思路

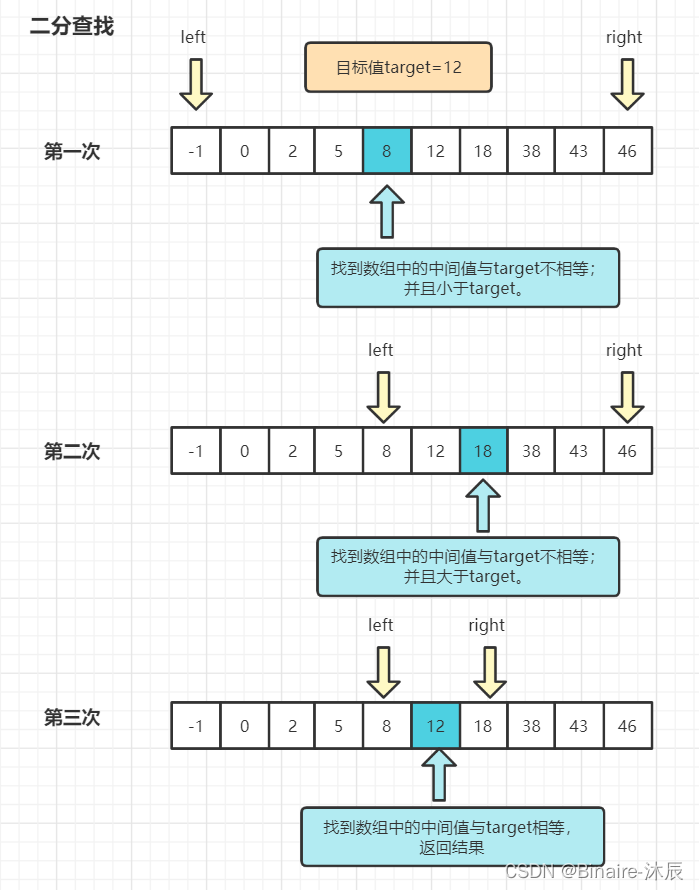
        以升序数列为例，比较目标元素与数列中间位置的元素的大小，如果目标元素比中间位置的元素大，则继续在数列的后半部分中进行二分查找；如果目标元素比中间位置的元素小，则在数列的前半部分进行比较；如果相等，则找到了元素的位置。每次比较的数列长度都会是之前数列的一半，直到找到相等元素的位置或者最终没有找到目标元素。

图解

给定一个有序的升序排列的数组 nums=[-1，0，2，5，8，12，18，38，43，46]
然后在该数组中找到目标值 target = 12。
图解如下：

力扣原题

704.二分查找

题目描述：
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
1
2
3

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
1
2
3

解题思路：

根据题意得出该数组为有序数组，这也是使用二分查找的前提条件。

• 定义两个指针分别指向数组的首尾两个元素；
• 找到数组的中间值mid；
• 如果nums[mid] < target，则 target 位于数组的后半部分，反之nums[mid] > target在前半部分；
• 重复上一步操作，直到nums[mid] = target，说明找到target，返回下标即可。

Java代码实现：

class Solution {
    public int search(int[] nums, int target) {
        int left = 0,right = nums.length - 1;
        while(left <= right) { // 循环条件
            int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1;  // 找不到则返回-1
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

复杂度分析：

• 时间复杂度：O(logn)，其中 n 是数组的长度。

• 空间复杂度：O(1)。