Week 7 Latent Variable Models and Expectation Maximization

Week 7 Latent Variable Models and Expectation Maximization
目录

一、Clustering

1、Clustering Algorithms（聚类算法）

2、软聚类和硬聚类

二、KMeans Algorithm（简单易懂版）- 硬聚类

1、KMeans原理

2、KMeans过程

3、KMeans算法实例讲解

三、KMeans Algorithm（课件公式推导版）

1、“1-of-K”⽬标函数

2、编辑的最优化和编辑的最优化（包含公式推导）

四、Latent Variable Models（潜变量模型）

五、Expectation-Maximization（EM）

1、EM算法简介

2、EM算法的基本步骤

六、Gaussian Mixture Models（GMM）

1、混合高斯的综述

2、似然函数 for GMM

3、最大化Log-Likelihood

4、EM for GMM的最优参数值

5、EM for GMM执行步骤

一、Clustering

1、Clustering Algorithms（聚类算法）
- 基于中心（KMeans）
- 基于密度 (DBSCAN)（Density based）
- 层次聚类（Hierarchical clustering）
- 基于图的聚类（Graph based clustering）
2、软聚类和硬聚类
- 软聚类：数据点可能属于一个或多个集群，且给出属于每个集群的概率
- 硬聚类：数据点只属于一个集群
二、KMeans Algorithm（简单易懂版）- 硬聚类

1、KMeans原理

K-Means算法的特点是类别的个数是人为给定的，如果让机器自己去找类别的个数，通过一次次重复这样的选择质心-计算距离后分类-再次选择新质心的流程，直到我们分组之后所有的数据都不会再变化了，也就得到了最终的聚合结果。
- KMeans 对初始值敏感，这意味着具有不同初始聚类中心的 Kmeans 的不同执行可能会导致不同的解决方案
- KMeans 是一种非概率算法，仅支持硬分配，一个数据点只能分配给一个且只有一个集群
2、KMeans过程
- 随机选取k个质心（k值取决于你想聚成几类）
- 计算样本到质心的距离，距离质心距离近的归为一类，分为k类
- 求出分类后的每类的新质心
- 再次计算计算样本到新质心的距离，距离质心距离近的归为一类
- 判断新旧聚类是否相同，如果相同就代表已经聚类成功，如果没有就循环2-4步骤直到相同
3、KMeans算法实例讲解
- 随机选取k个质心（k值取决于你想聚成几类）
假设我想聚3类，那我们随机选取【电影1、电影6、电影9】这3个电影作为质心（初始大佬）
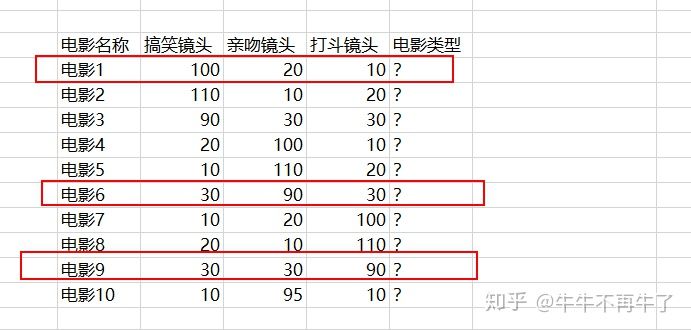
- 计算样本到质心的距离，距离质心距离近的归为一类，分为k类
计算除质心（大佬）外的样本（小弟）的欧式距离，样本（小弟）离哪个质心（大佬）近，该样本就跟哪个质心（大佬）

从上图可以看出：

电影2、电影3（小弟）离电影1（大佬）更近，所以他们3个暂时为A类

电影4、电影5、电影10（小弟）离电影6（大佬）更近，所以他们4个暂时为B类

电影7、电影8（小弟）离电影9（大佬）更近，所以他们3个暂时为C类
- 求出分类后的每类的新质心
上面我们已经分为三类了，我们需要从三类中重新选出大佬（质心）。

A将电影2、电影3和电影1的平均值做A类的大佬，则A类新大佬（质心）为：

电影搞笑镜头电影搞笑镜头电影搞笑尽头=(电影1搞笑镜头+电影2搞笑镜头+电影3搞笑尽头3,

电影亲吻镜头电影亲吻镜头电影亲吻尽头，电影1亲吻镜头+电影2亲吻镜头+电影3亲吻尽头3，

电影打斗镜头电影打斗镜头电影打斗尽头电影1打斗镜头+电影2打斗镜头+电影3打斗尽头3)

=(100,20,20)

同理也可以计算出B类新大佬（质心）为（17.5，98.75，17.5），C类新大佬（20,20,100）
- 再次计算计算样本到新质心的距离，距离质心距离近的归为一类
同样用上面方法计算样本到质心（新大佬）的欧式距离，得

从上图可以看出：

电影1、电影2、电影3（小弟）离A类（新大佬）更近，他们归为一类

电影6、电影4、电影5、电影10（小弟）离B类（新大佬）更近，他们也归为一类

电影9、电影7、电影8（小弟）离C类（新大佬）更近，他们也归为一类
- 判断新旧聚类是否相同
经过这次计算我们发现聚类情况并没有变化，这就说明我们的计算收敛已经结束了，不需要继续进行分组了，最终数据成功按照相似性分成了三组。即电影1，2,3为一类电影4,5，6，10为一类，电影7,8，9为一类，完成聚类。

三、KMeans Algorithm（课件公式推导版）

1、“1-of-K”⽬标函数

引⼊⼀组 D 维向量 $\mu_k$ ，其中 k = 1 , . . . , K ，且 µ k是与第k个聚类关联的⼀个代表。正如我们将看到的那样，我们可以认为 $\mu_k$ 表⽰了聚类的中⼼。我们的⽬标是找到数据点分别属于的聚类，以及⼀组向量{ $\mu_k$ }，使得每个数据点和与它最近的向量 $\mu_k$ 之间的距离的平⽅和最⼩。

现在，⽐较⽅便的做法是定义⼀些记号来描述数据点的聚类情况。对于每个数据点，我们引⼊⼀组对应的 ⼆值指⽰变量 $r_{nk}$ ∈ {0, 1} ，其中 k = 1 , . . . , K表⽰数据点属于K 个聚类中的哪⼀个， 从⽽如果数据点xn被分配到类别k，那么 $r_{nk}$ = 1 ， 且对于j ≠ k，有 $r_{nk}$ = 0 。这被称为“ 1-of-K ”表⽰⽅式。之后我们可以定义⼀个⽬标函数，有时被称为 失真度量（distortion measure ），形式为:

$J=\sum_{n=1}^{N} \sum_{k=1}^{K} r_{n k}\left\|\boldsymbol{x}_{n}-\boldsymbol{\mu}_{k}\right\|^{2}$
它表⽰每个数据点与它被分配的向量 $\mu_k$ 之间的距离的平⽅和。我们的⽬标是找

到 { $r_{nk}$ } 和 { $\mu_k$ } 的值，使得 J 达到最⼩值。我们可以⽤⼀种迭代的⽅法完成这件事，其中每次迭

代涉及到两个连续的步骤，分别对应 $r_{nk}$ 的最优化和 $\mu_k$ 的最优化。

2、 $r_{nk}$ 的最优化和 $\mu_k$ 的最优化（包含公式推导）

（1）步骤
- ⾸先，我们为 $\mu_k$ 选择⼀些初始值。
- 然后，在第⼀阶段，我们关于 $r_{nk}$ 最⼩化J，保持 $\mu_k$ 固定。（E）
- 在第⼆阶段，我们关于 $\mu_k$ 最⼩化J，保持 $r_{nk}$ 固定。（M）
- 不断重复这个⼆阶段优化直到收敛。
我们会看到， 更新 $r_{nk}$ 和更新 $\mu_k$ 的两个阶段分别对应于EM算法中的E（期望）步骤和M（最⼤化）步骤 。为了强调这⼀点，我们会在K 均值算法中使⽤ E 步骤和 M 步骤的说法。

（2）E（期望）步骤

⾸先考虑确定 $r_{nk}$ 。上述给出的 J 是 $r_{nk}$ 的⼀个线性函数，因此最优化过程可以很容易地进⾏，得到⼀个解析解。与不同的n 相关的项是独⽴的，因此我们可以对每个 n 分别进⾏最优化， 只要k的值使 $\left \| x_n - \mu_k \right \|^2$ 最⼩，我们就令 $r_{nk}$ 等于1 。换句话说，我们可以简单地将数据点的聚类设置为最近的聚类中⼼。更形式化地，这可以表达为:

（3） M（最⼤化）步骤

现在考虑 $r_{nk}$ 固定时，关于 $\mu_k$ 的最优化。⽬标函数J是 $\mu_k$ 的⼀个⼆次函数，令它关于 $\mu_k$ 的导

数等于零，即可达到最⼩值，即：

$\begin{gathered} 2 \sum_{n=1}^{N} r_{n k}\left(\boldsymbol{x}_{n}-\boldsymbol{\mu}_{k}\right)=0 \\ \boldsymbol{\mu}_{k}=\frac{\sum_{n} r_{n k} \boldsymbol{x}_{n}}{\sum_{n} r_{n k}} \end{gathered}$

这个表达式的分母等于聚类 k 中数据点的数量，因此这个结果有⼀个简单的含义，即令

$\mu_k$ 等于类别k的所有数据点的均值 。因此，上述步骤被称为 K 均值（ K - means ）算法。

重新为数据点分配聚类的步骤以及重新计算聚类均值的步骤重复进⾏，直到聚类的分配不改

变（或者直到迭代次数超过了某个最⼤值） 。由于每个阶段都减⼩了⽬标函数 J 的值，因此算

法的收敛性得到了保证。然⽽， 算法可能收敛到J的⼀个局部最⼩值⽽不是全局最⼩值。

（4）KMeans中执行EM算法的例子

进行四轮EM后数据收敛：
四、Latent Variable Models（潜变量模型）

潜变量模型就是一种复杂的概率模型。简单的说，如果概率模型 p(x;θ) 对随机变量 x 的分布建模，且具有(离散变量和连续变量形式)：

$\begin{gathered} p(x ; \theta)=\sum_{z} p(x, z ; \theta)=\sum_{z} p(z ; \theta) p(x \mid z ; \theta) \\ p(x ; \theta)=\int p(x, z ; \theta) d z=\int p(z ; \theta) p(x \mid z ; \theta) d z \end{gathered}$

的形式，这样的模型就被称为潜变量模型，其中 z 称为潜变量， x 称为观测变量。当 z 为离散型随机变量时，称为离散型潜变量模型，当 z 为连续型随机变量时，模型称为连续型潜变量模型。对于随机向量 X 和 Z 的情况，道理相同。

也就是说，潜变量模型是通过对某个联合分布进行边缘化得到的一个概率模型。被边缘化的随机变量（或向量）就是潜变量。因此，潜变量模型是一种基于简单的分布形式构建复杂的分布形式的方法，具有更高的复杂度，表示能力更强。但它的极大似然估计更为困难，因为函数形式中包含求和或积分操作。

假设潜变量模型一个简单随机样本为 X={x1,⋯,xN} ，则其对数似然函数为（离散变量和连续变量形式）

$\begin{aligned} &\ln p(X ; \theta)=\sum_{n=1}^{N} \ln \left\{\sum_{z} p\left(x_{n}, z ; \theta\right)\right\} \\ &\ln p(X ; \theta)=\sum_{n=1}^{N} \ln \left\{\int p\left(x_{n}, z ; \theta\right) d z\right\} \end{aligned}$

其中的求和或积分运算阻止了对数函数直接作用在联合分布 p(xn,z;θ)=p(z;θ)p(xn|z;θ) 之上，通常 p(z;θ) 和 p(xn|z;θ) 都是简单的分布形式。那么就无法通过求导得到极大似然估计的闭式解。

潜变量模型的一个著名的例子是高斯混合模型（Gaussian mixture model, GMM），它的函数形式如下:

$p(\mathbf{x} ; \Theta)=\sum_{k=1}^{K} \pi_{k} N\left(\mathbf{x} ; \mu_{k}, \Sigma_{k}\right)$

五、Expectation-Maximization（EM）

1、EM算法简介

EM算法最初作为一种处理含缺失值的情况下求概率模型极大似解的方法，在潜变量模型的极大似然估计问题上得到广泛的应用，因为潜变量模型中的潜变量（未观测变量）可被认为是一种缺失数据。假设除了观测样本X={x1,⋯,xN} 之外，还拥有潜变量 z 的数据 Z={z1,⋯,zN} ，二者合在一起称为完整数据（complete data）；观测变量的数据 X 自身被称为非完整数据（incomplete data）。如果拥有完整数据，则完整数据对数似然函数为

因为 z 和 x 通常具有简单的分布形式（属于指数家族），显然通过求导可得到模型参数 θ 的闭式解。然而通常并没有潜变量 z 的数据，只有非完整数据 X 。

EM算法是一种迭代算法，它的基本思想是，在当前参数的估计值 $\theta ^{(n)}$ 之下，通过极大化完整数据对数似然函数在潜变量 z 的后验分布下的期望来更新参数，求出 $\theta ^{(n+1)}$ 。

2、EM算法的基本步骤
- 初始化模型参数 $\theta ^{(0)}$ .
- E步。计算潜变量 z 在当前参数 $\theta ^{(n)}$ 下的后验分布 p(Z|X; $\theta ^{(n)}$ ) ，并求完整数据对数似然函数的期望
- M步。通过极大化 Q(θ， $\theta ^{(n)}$ ) 更新：
- 判断似然函数 ln⁡p(X;θ) 或模型参数 θ 收敛。不收敛则返回第2步。
其中，对于离散型潜变量模型来说，完整数据对数似然函数的期望为

对于连续型型潜变量模型来说，完整数据对数似然函数的期望为

EM算法通过迭代地最大化完整数据对数似然函数的期望使问题简化，因为完整数据对数似然函数是容易求解的，只要 p(z;θ) 和 p(x|z;θ) 具有简单分布形式。

六、Gaussian Mixture Models（GMM）

1、混合高斯的综述

我们将⾼斯混合模型看成⾼斯分量的简单线性叠加，⽬标是提供⼀类⽐单独的⾼斯分布更强⼤的概率模型。我们现在使⽤离散潜在变量来描述⾼斯混合模型。 ⾼斯混合概率分布可以写成⾼斯分布的线性叠加的形式 ，即：

$p(\boldsymbol{x})=\sum_{k=1}^{K} \pi_{k} \mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k}\right)$

其中参数{ $\pi _k$ }必须满⾜：

$\begin{gathered} p\left(z_{k}=1\right)=\pi_{k} \\ 0 \leq \pi_{k} \leq 1 \\ \sum_{k=1}^{K} \pi_{k}=1 \end{gathered}$

使得概率是⼀个合法的值。 由于z使⽤了“1-of-K”表⽰⽅法 ，因此我们也可以将这个概率分布写

成：

联合概率分布为 p ( z ) p ( x | z ) ，从⽽ x 的边缘概率分布可以通过将联合概率分布对所有可能的 z 求

和的⽅式得到，即： （x的边缘概率分布公式）

$\begin{aligned} \gamma\left(z_{k}\right) \equiv p\left(z_{k}=1 \mid \boldsymbol{x}\right) &=\frac{p\left(z_{k}=1\right) p\left(\boldsymbol{x} \mid z_{k}=1\right)}{\sum_{j=1}^{K} p\left(z_{j}=1\right) p\left(\boldsymbol{x} \mid z_{j}=1\right)} \\ &=\frac{\pi_{k} \mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k}\right)}{\sum_{j=1}^{K} \pi_{j} \mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_{j}, \boldsymbol{\Sigma}_{k}\right)} \end{aligned}$

我们将 $\pi _k$ 看成 = 1 的先验概率，将 $\gamma (z_k)$ 看成观测到 x之后，对应的后验概率。正如我们将看

到的那样， $\gamma (z_k)$ 也可以 被看做分量k对于“解释”观测值x的“责任”（responsibility）。

2、似然函数 for GMM

（1）对于非完整数据（incomplete data）而言，我们有如下公式：（课件里重点讲的，下面的3、4也只是针对数据 X 自身）

（2）对于完整数据（complete data）而言，我们有如下公式：

3、最大化Log-Likelihood

对上面的似然函数求导：

从⽽第k个分量的混合系数为那个分量对于解释数据点的“责任”的平均值。

4、EM for GMM的最优参数值

5、EM for GMM执行步骤
相关阅读:
spring cloud
【论文笔记】Aleph_star
【笔记】ssh link-local 地址登录
 【Java】Math 类
 公网远程访问本地Jupyter Notebook服务
 Nginx的安装
 带权有向图最短路径之Dijkstra和Floyd
Windows 本地安装 Mysql8.0
Python：最低要求
 机器人种类知多少
原文地址：https://blog.csdn.net/wangjian530/article/details/126152769

一、Clustering

1、Clustering Algorithms（聚类算法）

2、软聚类和硬聚类

二、KMeans Algorithm（简单易懂版）- 硬聚类

1、KMeans原理

2、KMeans过程

3、KMeans算法实例讲解

三、KMeans Algorithm（课件公式推导版）

1、“1-of-K”⽬标函数

2、的最优化和的最优化（包含公式推导）

四、Latent Variable Models（潜变量模型）

五、Expectation-Maximization（EM）

1、EM算法简介

2、EM算法的基本步骤

六、Gaussian Mixture Models（GMM）

1、混合高斯的综述

2、似然函数 for GMM

3、最大化Log-Likelihood

4、EM for GMM的最优参数值

5、EM for GMM执行步骤

2、 $r_{nk}$ 的最优化和 $\mu_k$ 的最优化（包含公式推导）