-
矩阵分析与应用(19)
学习来源:《矩阵分析与应用》 张贤达 清华大学出版社
奇异值分解
一、奇异值分解及其解释
1. 定理(矩阵的奇异值分解)
令
 (或
(或 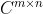 ),则存在正交矩阵(或酉矩阵)
),则存在正交矩阵(或酉矩阵) 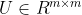 (或
(或 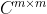 )和
)和 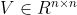 (或
(或 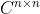 )使得
)使得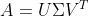 (或
(或 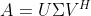 )
)式中
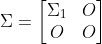
且
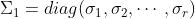 ,其余对角元素按照顺序
,其余对角元素按照顺序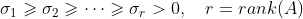
排列。
2. 定义
若
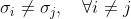 ,则矩阵
,则矩阵  的奇异值
的奇异值 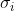 称为单奇异值。
称为单奇异值。3. 奇异值和奇异值分解的解释
1)
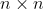 矩阵
矩阵  为酉矩阵,在式
为酉矩阵,在式 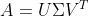 两边右乘
两边右乘  ,得到
,得到 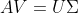 ,其列向量形式为
,其列向量形式为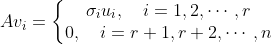
因此,
 的列向量
的列向量 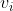 称为矩阵
称为矩阵  的右奇异向量,
的右奇异向量, 称为
称为  的右奇异向量矩阵。
的右奇异向量矩阵。2)
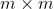 矩阵
矩阵 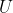 是酉矩阵,在式
是酉矩阵,在式 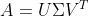 两边左乘
两边左乘 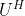 ,得到
,得到  ,其列向量形式为
,其列向量形式为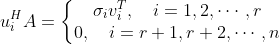
因此,
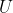 的列向量
的列向量 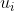 称为矩阵
称为矩阵  的左奇异向量,并称
的左奇异向量,并称 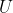 为
为  的左奇异向量矩阵。
的左奇异向量矩阵。3)矩阵
 的奇异值分解式
的奇异值分解式 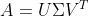 可以改写为向量表达式:
可以改写为向量表达式: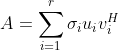
这种表达式称为
 的并向量(奇异值)分解。
的并向量(奇异值)分解。4)由式
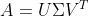 可得
可得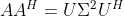
这表明,
 矩阵
矩阵  的奇异值
的奇异值 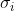 是矩阵乘积
是矩阵乘积 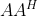 的特征值的正平方根。
的特征值的正平方根。5)当矩阵
 的秩
的秩 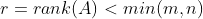 时,由于奇异值
时,由于奇异值 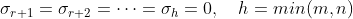 ,因此奇异值分解公式可以简化为
,因此奇异值分解公式可以简化为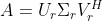
式中,
![U_r=[u_1,u_2,\cdots ,u_r],\quad V_r=[v_1,v_2,\cdots ,v_r],\quad \Sigma_r=diag(\sigma_1,\sigma_2,\cdots ,\sigma_r)](https://1000bd.com/contentImg/2022/08/09/113543453.gif)
式
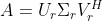 被称为矩阵
被称为矩阵  的截尾奇异值分解或薄奇异值分解。与之相对地,式
的截尾奇异值分解或薄奇异值分解。与之相对地,式 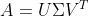 称为全奇异值分解。
称为全奇异值分解。6)若矩阵
 具有秩
具有秩 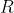 ,则
,则①
 酉矩阵
酉矩阵 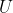 的前
的前 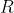 列组成矩阵
列组成矩阵  的列空间的标准正交基。
的列空间的标准正交基。②
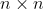 酉矩阵
酉矩阵  的前
的前 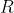 列组成矩阵
列组成矩阵  的行空间(或
的行空间(或 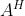 的列空间)的标准正交基。
的列空间)的标准正交基。③
 的后
的后 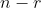 列组成矩阵
列组成矩阵  的零空间的标准正交基。
的零空间的标准正交基。④
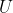 的后
的后 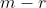 列组成矩阵
列组成矩阵 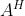 的零空间的标准正交基。
的零空间的标准正交基。3. 奇异值的内在含义
当原
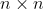 矩阵
矩阵  有一个零奇异值时,该矩阵的秩
有一个零奇异值时,该矩阵的秩  ,即原矩阵
,即原矩阵  本来就不是满秩的。因此,如果一个正方矩阵具有零奇异值,则该矩阵必定是奇异矩阵。
本来就不是满秩的。因此,如果一个正方矩阵具有零奇异值,则该矩阵必定是奇异矩阵。一个正方矩阵只要有一个奇异值接近零,那么这个矩阵就接近于奇异矩阵。推而广之,一个非正方的矩阵如果有奇异值为零,则说明这个长方矩阵一定不是列满秩的或者行满秩的。这种情况称为矩阵的秩亏缺,它相对于矩阵的满秩是一种奇异现象。
无论是正方还是长方矩阵,零奇异值都刻画矩阵的奇异性,这就是矩阵奇异值的内在含义。
二、奇异值的性质
1. 矩阵变形与奇异值的关系
令矩阵
 和
和 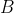 均为
均为 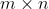 矩阵,且
矩阵,且 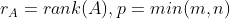 。
。设矩阵
 的奇异值排列为
的奇异值排列为
并且用
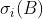 表示矩阵
表示矩阵 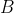 的第
的第 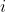 个大奇异值。则矩阵的各种变形与奇异值有以下关系:
个大奇异值。则矩阵的各种变形与奇异值有以下关系:1)
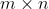 矩阵
矩阵  的共轭转置
的共轭转置 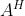 的奇异值分解为
的奇异值分解为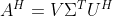
即矩阵
 和
和 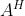 具有完全相同的奇异值。
具有完全相同的奇异值。2)
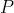 和
和 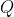 分别为
分别为 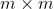 和
和 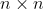 酉矩阵时,
酉矩阵时,  的奇异值分解为
的奇异值分解为
其中,
 。也就是说,矩阵
。也就是说,矩阵  与
与  具有相同的奇异值,即奇异值具有酉不变性,但奇异向量不同。
具有相同的奇异值,即奇异值具有酉不变性,但奇异向量不同。3)
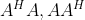 的奇异值分解分别为
的奇异值分解分别为
其中

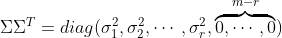
4)
 矩阵
矩阵  的奇异值分解与
的奇异值分解与  维 Moose-Penrose 广义逆矩阵
维 Moose-Penrose 广义逆矩阵 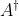 之间存在以下关系:
之间存在以下关系: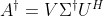
其中,
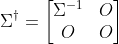 。
。 -
相关阅读:
JUC五-ForkJoin,JMM和volatile,CAS,自旋锁,死锁
Mysql报错:1130-host ... is not allowed to connect to this MySql server如何处理
Java 复习笔记 - 常见算法:API Arrays
Java程序中常用的设计模式有哪些和该种设计模式解决的痛点
Spring Boot 中的审计
java springboot 如何实现小程序支付
【数据结构与算法】LinkedList与链表(上)
TMall商城系统订单模块分析(3)
详解设计模式:单例模式
揭开MyBatis的神秘面纱:掌握动态代理在底层实现中的精髓
- 原文地址:https://blog.csdn.net/qq_40206924/article/details/126141869