Tips: 采用java语言,关注博主,底部附有完整代码

工具:IDEA

本系列介绍的是数据结构: 树

这是第四篇目前计划一共有12篇:

1. 二叉树入门
2. 顺序二叉树
3. 线索化二叉树
4. 堆排序 (本篇)
5. 赫夫曼树(一)
6. 赫夫曼树(二)
7. 赫夫曼树(三)
8. 二叉排序树
9. 平衡二叉树
10. 2-3树,2-3-4树,B树 B+树 B*树 了解
11. 红黑树(一)
12. 红黑树(二)

敬请期待吧~~

高光时刻

前沿:

本章应该和

• 排序算法一
• 排序算法二

放在一起的,可是当时对树的概念有点模糊,所以就没写,一直拖到现在…现在剑已锋利,那就写写喽

大顶堆与小顶堆

大顶堆

可以看到,如果是大顶堆,那么当前结点比左子 / 右子结点大

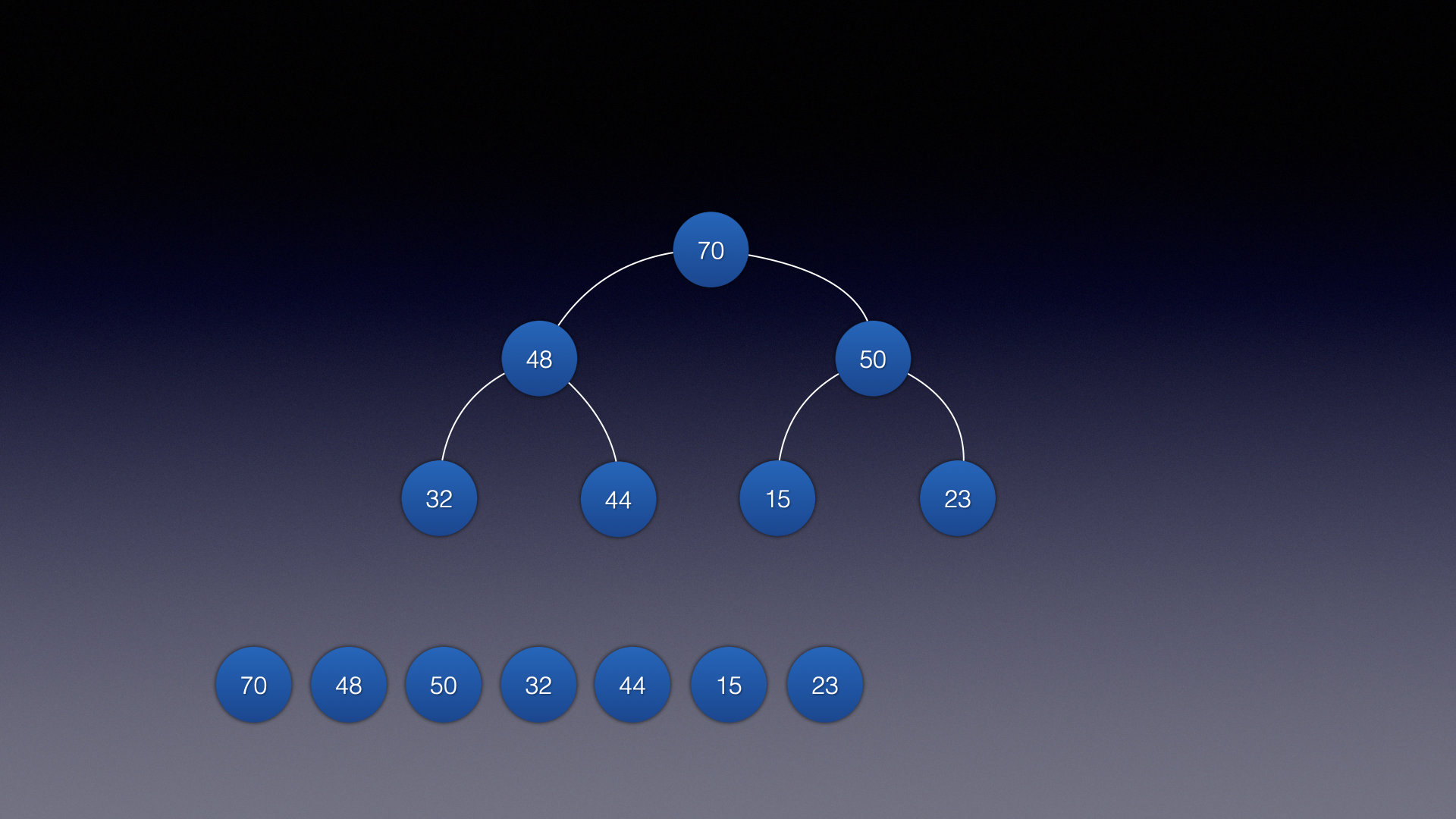
例如 结点48

• 比左子结点32大
• 比右子结点44大

所以在大顶堆中,根节点是最大的!

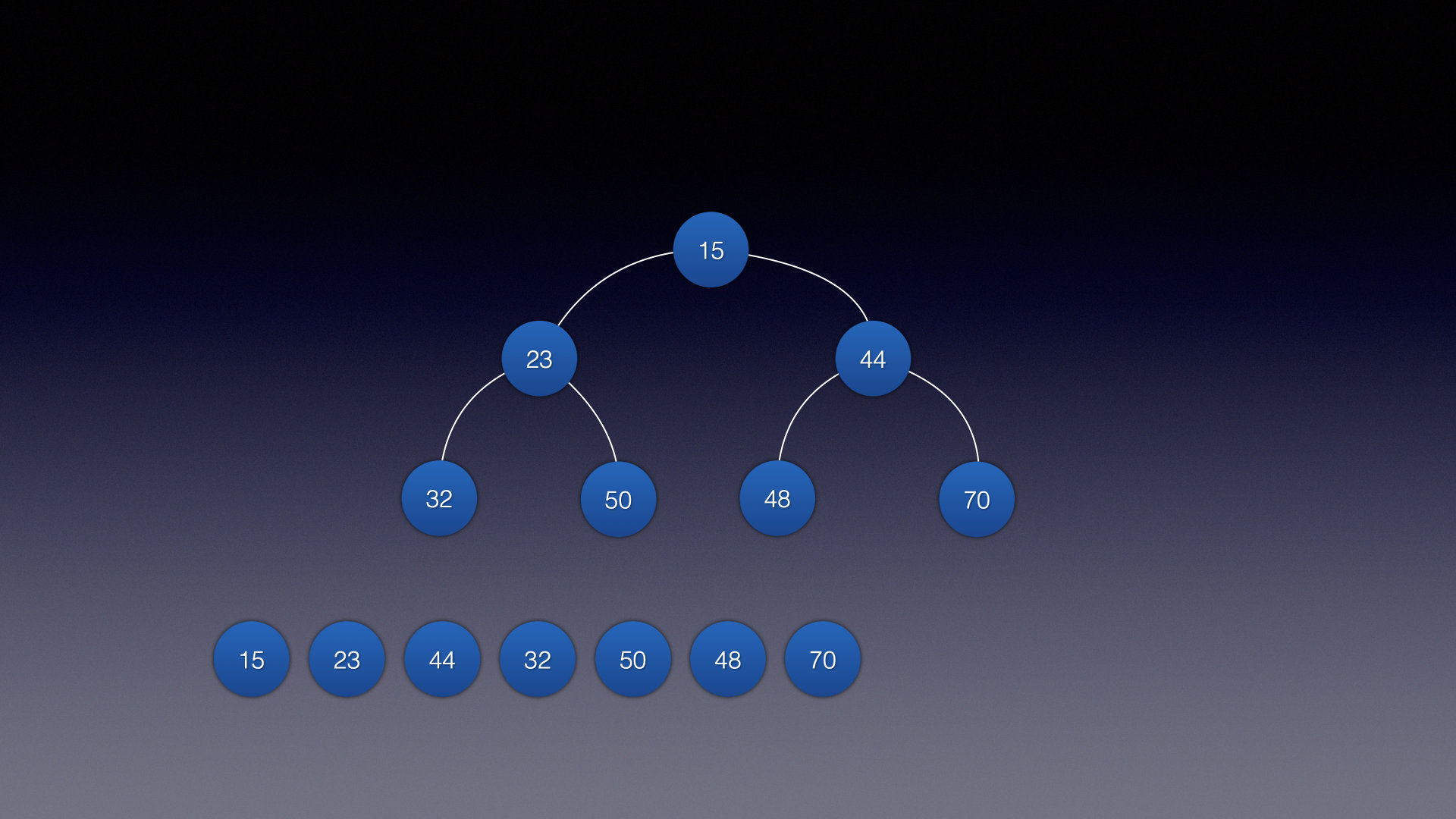
小顶堆

小顶堆的概念和大顶堆一样!

第二张辅助图:

回顾

在第二篇: 数据结构与算法:树 顺序存储二叉树(二)中提到一个概念,在这里有很大的作用,来回顾一下

先通过数组构建一颗树,切记这个流程只是在你脑海里的过程!

只是想象成这样便于理解罢了!

当前树结构是这样的:

n = 1 n是下标

那么n对应的值就是50

• 他的左子结点是2 * n + 1 = 3, 对应的值就是70
• 他的右子节点是 2 * n + 2 = 4 对应的值就是32
• 他的父结点是 (n - 1) / 2 = 0 对应的值是23

如果清晰这几个概念,堆排序就好办多了

分析

来分析一下,如何通过‘想象’的树的结构来排列数组

他其实思路很简单, 在堆排序过程中,一直排列的是父结点

因为排列的是父结点,所以他一定有子结点,就可以通过

• 2n + 1 获取左子结点
• 2n + 2 获取右子结点

还是以这张图为例:

那么他循环的节点就是 48, 50,23

假设第一次循环的节点是48,那么此时n就是2

• 左子节点: 2n + 1 = 5 对应的值就是15
• 右子节点: 2n + 2 = 6 对应的值就是44

那么只需要判断左子 / 右子结点和当前结点那一个值更大,替换到n = 2的位置即可,很显然此时48就是最大的

第二次循环结点是50

• 左子节点: 2n + 1 = 3 对应的值就是70
• 右子节点: 2n + 2 = 4 对应的值就是32

很明显,左子结点才是最大的值,那么只需要将ints[3] 和 ints[1]的位置交换一下即可

交换完成之后就变成了这样

第三次循环结点是23

• 左子节点: 2n + 1 = 1 对应的值就是70
• 右子节点: 2n + 2 = 2 对应的值就是48

很明显,左子结点才是最大的值,那么只需要将ints[0] 和 ints[1]的位置交换一下即可

效果图为:

可以看出此时根节点70就是最大的值!

但是细心的同学肯定发现了一个问题,这也不是大顶堆啊,

下标1明显比他的左子 / 右子结点小

所以这里还需要运用到递归,使这棵树为大顶堆

这里还需要将ints[3] 和 ints[1]交换

交换后效果图为:

现在这棵树就是一个大顶堆了!

此时只需要将ints[0] 和最后一个交换ints[6],那么最大的值就始终保持在了最后面

当然,交换过后,这个数就不参加下一次的排序

然后通过递归,依次构建成大顶堆

最后在依次的交换到最后的位置

那么后面的值就是大的,前面的值就是小的

最终形成了从小到大的排序效果

来看一眼交换流程:

完整代码

详细完整流程:

完整代码:

/**
 * @author: android 超级兵
 * @create: 2022-06-09 10:01
 * TODO 堆排序
 * 10万个数据预计耗时13毫秒
 **/
public class Client {
    public static void main(String[] args) {
        int[] ints = {23, 50, 48, 70, 32, 15, 44};

        long oldTime = System.currentTimeMillis();
        // 实战
        sort(ints);

        System.out.println("耗时:" + PrintUtil.transform(System.currentTimeMillis() - oldTime));
        System.out.println("排序完成，结果为：" + Arrays.toString(ints));
    }


    /*
     * @author: android 超级兵
     * @create: 2022/6/10 13:32
     * TODO 堆排序
     */
    public static void sort(int[] ints) {

        int length = ints.length;

        // 倒叙输出父结点(构建大顶堆)
        for (int i = length / 2 - 1; i >= 0; i--) {
            // 根据父结点来排序(父结点，左子结点，右子结点)，要满足大顶堆需求
            // 构建大顶堆
            adjustHeap(ints, i, length);
        }

        System.out.println("构建完成，大顶堆为:" + Arrays.toString(ints));

        // 由大顶堆特性可知，如果是一个正确的大顶堆，那么根节点就是最大值
        // 根节点移动到最后一位，此时最后一位是最大值，不参与下一次循环，依次达到排序作用

        int temp;
        // 交换 顶部位置和最后一个位置
        for (int i = length - 1; i > 0; i--) {
            // 第一位和最后一位交换
            temp = ints[0];
            ints[0] = ints[i];
            ints[i] = temp;

            // 在次构建大顶堆 使根节点为最大值!
            adjustHeap(ints, 0, i);
        }
    }

    /**
     * 为了满足大顶堆需求!
     *
     * @param ints   查询的数组
     * @param i      当前最后一个父结点
     * @param length 数组长度
     */
    public static void adjustHeap(int[] ints, int i, int length) {

        // 记录根结点
        int temp = ints[i];

        System.out.println("父结点为:" + i);
        // 最后一个父结点的
        // i 父节点
        // i * 2 + 1 是i的左子结点 【 int j =  i * 2 + 1 】
        // i * 2 + 2 是i的右子结点 也可以表示为 j + 1
        for (int j = i * 2 + 1; j < length; j = j * 2 + 1) {

            // j 左子结点
            // j + 1 右子结点
            // 如果右子结点存在 并且左子结点 < 右子结点
            if (j + 1 < length && ints[j] < ints[j + 1]) {
                // 执行到这里 说明右子结点 > 左子结点
                // 那么就让 j = 右子结点
                j++;
            }

            // temp 是父节点
            // 现在j必然是 i的左子结点或右子结点，和跟节点做比较
            // 如果 子节点 > 父结点
            if (ints[j] > temp) {
                // 那么父结点 = 子节点
                ints[i] = ints[j];

                // 重点! 为了调整子结点到合适的位置！
                i = j;
            } else {
                break;
            }
        }
        // i 是父结点坐标
        // 此时i可能发生变化 可能是子结点坐标
        ints[i] = temp;

        System.out.println("排序中:" + Arrays.toString(ints) + "\t父结点坐标 = " + i);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

代码如果看不明白只能多看看分析流程,多debug走几遍,写博客只能尽量吧思路和细节说清楚,代码这东西每个人理解都不一样,而且单纯靠文字根本不可能说明白,反正我是看不明白文字!

所以只能加好注释然后说清楚过程即可…

完整代码

原创不易,您的点赞就是对我最大的支持!

下一篇:赫夫曼树(一) [开发中]