-
矩阵分析与应用
向量的内积与范数
根据元素的取值方式的不同,向量分为常数向量,函数向量和随机向量。常数向量是元素为常数的向量;函数向量是元素取某个变量的函数值的向量;而随机向量则是元素为随机变量的向量。
虽然常数向量,函数向量和随机向量的内积定义公式有所不同,但是无论向量取何种形式,向量的内积和范数都必须服从一定的公理。
由于实向量是复向量的特例,因此以下以复向量作为讨论对象,并用R与C表示实数域和复数域。
令V为复向量空间,函数
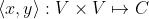 称为向量x和y的内积,对所有
称为向量x和y的内积,对所有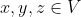 ,满足以下内积公理:
,满足以下内积公理:
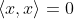 ,当且仅当x=0时
,当且仅当x=0时
 ,其中*表示复数共轭。
,其中*表示复数共轭。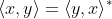 ,其中*表示复数共轭。
,其中*表示复数共轭。
令V为复向量空间,函数
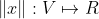 称为向量x的范数,对所有
称为向量x的范数,对所有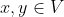 ,下面的范数公理成立:
,下面的范数公理成立:
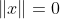 ,当且仅当x=0时
,当且仅当x=0时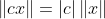

常数向量的内积与范数:
两个m*1维常数向量
![x=[x_{1},x_{2},.. .x_{m}]^{T}](https://1000bd.com/contentImg/2022/06/24/021648095.gif) 和
和![y=[y_{1},y_{2},.. .y_{m}]^{T}](https://1000bd.com/contentImg/2022/06/24/021648873.gif) 的内积(或叫点积)定义为:
的内积(或叫点积)定义为: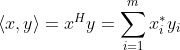
两个向量之间的夹角定义为:

若
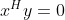 ,则
,则 ,此时称常数向量x与y正交。
,此时称常数向量x与y正交。若两个常数向量的内积等于0,则称为正交,即
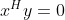 ,记作
,记作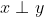 。零向量0与同一空间的任何向量都正交。
。零向量0与同一空间的任何向量都正交。下面是几种常用的向量范数。
1.
 范数,也叫范数或1范数。
范数,也叫范数或1范数。
2.
 范数,这一范数常称Euclidean范数,有时也称Frobenius范数。
范数,这一范数常称Euclidean范数,有时也称Frobenius范数。
3.
 范数,也称无穷范数或极大范数。
范数,也称无穷范数或极大范数。
4.
 范数.
范数.
当p=2时,
 范数与Euclidean范数完全等价。
范数与Euclidean范数完全等价。无穷范数是
 范数的极限形式,即有:
范数的极限形式,即有:
假定向量x和y有共同的起点,它们的端点分别为x和y,则
 度量两个向量x,y两个端点之间的标准Euclidean距离。特别的,非负的标量
度量两个向量x,y两个端点之间的标准Euclidean距离。特别的,非负的标量 称为向量x的Euclidean长度。Euclidean长度为1的向量叫做归一化向量。
称为向量x的Euclidean长度。Euclidean长度为1的向量叫做归一化向量。对于任何不为零的向量
 ,向量
,向量 都是归一化的,并且它与x同方向。
都是归一化的,并且它与x同方向。常数向量W和V的外积(又叫叉积)记作
 ,定义为:
,定义为:
-
相关阅读:
大数据培训-DolphinScheduler(二)
抽象类和抽象方法
“我“是一名测试/开发程序员,小孙的内心独白......
Android软键盘windowSoftInputMode的使用与原理(使用篇)
c语言练习63:用malloc开辟二维数组的三种办法
XXXX项目管理目标(某项目实施后基于软件工程的总结)
C语言之指针详解
MySQL|子查询
生成.pkl文件,读取.pkl文件的内容
saas化调研
- 原文地址:https://blog.csdn.net/weixin_46007132/article/details/125411826