写在前面
参考文献:
《算法竞赛进阶指南》
动态规划算法的优化技巧 毛子青
c++ DP总结
一. 环形与后效性处理
我们都知道,一个题能用
- 无后效性
- 最优子结构
但对于有些题目,如果要用
所谓环形与后效性,即状态的转移与
举个例子,状态的转移可以从左到右,也可以从右到左,但
当状态初能够由状态末转移而来(此时构成了一个环形)时,此时称此
对于前者的处理,我们通常会改变
对于后者,我们通常对初始状态分类讨论,找出几种不是环形的
例题
后效性
本题的高斯消元处理
设
显然,我们
#include 环形
设计状态
如果我们直接转移的话,初始状态的睡或不睡会影响后面的转移(环形),所以分类讨论:
- 当初始状态为醒的时候(正常转移):
其中
- 当初始状态为睡的时候(此时要将初始休息的时间算上):
其中
最后将两个答案合并起来即可;
可以发现,对于环形的分类讨论,状态转移方程基本一样,但初始化会有差异;
另外,此题有空间的限制,需要把
#include 二. 倍增优化
倍增优化的关键是找出一个可以随意划分的状态,最后对状态进行拼接得到答案;
所谓随意划分,即此状态可以拆分成任意多个长度为
为什么一个状态能够随意划分成任意多个长度为
对于任意一个正整数,我们可以给他转变成一个二进制数,我们知道,一个二进制数可以表示成
例题
Luogu P1081 [NOIP2012 提高组] 开车旅行
本题有三个关键信息:已行驶的天数,所在城市,小A和小B各自行驶的路程长度;
若已知出发城市与天数,即可求得小A和小B各自行驶的路程长度,并且依据题意,天数还能反映谁现在在开车,所以我们可以把“天数” 作为“阶段”进行状态设计;
定义
很显然,这样开会炸内存,而天数又可以随意划分,可以考虑倍增优化;
重定义
其中
对于初始化,我们现在知道谁先开车,要求到那个城市,只需知道小A或小B在某一个城市时,下一个会到哪里即可,可以预处理出两个数组
对于问题
对于问题
则:
- 对于预处理
因为小A和小B只能往后走,所以我们可以从后往前遍历,并同时维护一个单调递增的序列(可以用 其实应该是平衡树,但我不会,每次只需找当前节点旁边一位或两位的最小值和次小值即可(建议参考下面的代码);
- 对于初始化
- 对于状态转移方程
- 对于
对于
- 对于
这里
#include p;
void init() {
p.insert({0, 9999999999999999});
p.insert({0, 9999999999999999});
p.insert({n + 1, -9999999999999999});
p.insert({n + 1, -9999999999999999}); //防止访问越界
for (long long i = n; i >= 1; i--) {
long long ga, gb;
p.insert({i, h[i]});
multiset::iterator q = p.lower_bound({i, h[i]});
q--;
long long lid = (*q).id, lh = (*q).he;
q++;
q++;
long long rid = (*q).id, rh = (*q).he;
q--;
if (abs(rh - h[i]) >= abs(lh - h[i])) {
gb = lid;
q--; q--;
if (abs(rh - h[i]) < abs((*q).he - h[i])) {
ga = rid;
} else {
ga = (*q).id;
}
} else {
gb = rid;
q++; q++;
if (abs((*q).he - h[i]) < abs(lh - h[i])) {
ga = (*q).id;
} else {
ga = lid;
}
}
f[0][i][0] = ga;
f[0][i][1] = gb;
da[0][i][0] = abs(h[ga] - h[i]);
db[0][i][1] = abs(h[gb] - h[i]);
}
}
pair<long long, long long> w(long long s, long long x) {
long long p = s;
long long la = 0;
long long lb = 0;
for (int i = 17; i >= 0; i--) {
if (f[i][p][0] && la + lb + da[i][p][0] + db[i][p][0] <= x) {
la += da[i][p][0];
lb += db[i][p][0];
p = f[i][p][0];
}
}
return {la, lb};
}
int main() {
cin >> n;
for (long long i = 1; i <= n; i++) cin >> h[i];
cin >> x0;
cin >> m;
init();
long long tt = 10;
for (int i = 1; i <= 17; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 0; k <= 1; k++) {
if (i == 1) {
f[i][j][k] = f[0][f[0][j][k]][1 - k];
da[i][j][k] = da[0][f[0][j][k]][1 - k] + da[0][j][k];
db[i][j][k] = db[0][f[0][j][k]][1 - k] + db[0][j][k];
} else {
f[i][j][k] = f[i - 1][f[i - 1][j][k]][k];
da[i][j][k] = da[i - 1][j][k] + da[i - 1][f[i - 1][j][k]][k];
db[i][j][k] = db[i - 1][j][k] + db[i - 1][f[i - 1][j][k]][k];
}
}
}
}
long double ans = 1.00 * 0x3f3f3f3f;
long long an = 0;
for (int i = 1; i <= n; i++) {
pair<long long, long long> a = w(i, x0);
long long la = a.first;
long long lb = a.second;
if (lb == 0) continue;
long double d = 1.00 * la / (1.00 * lb);
if (d < ans) {
ans = d;
an = i;
} else if (d == ans) {
if (h[an] < h[i]) an = i;
}
}
cout << an << endl;
long long a, b;
for (int i = 1; i <= m; i++) {
cin >> a >> b;
pair<long long, long long> c = w(a, b);
cout << c.first << ' ' << c.second << endl;
}
return 0;
}
一般在设计出状态以后,发现空间复杂度不符合要求,且有状态能够随意划分,则可以使用倍增优化;
三. 数据结构优化
适用范围:
-
时间复杂度能够忍受
-
状态转移方程中要维护
一般使用线段树或树状数组
例题
Luogu P4644 [USACO05DEC] Cleaning Shifts S
我们可以定义
我们发现,
时间复杂度:
考虑优化;
发现状态转移方程有这一项:
对于一个区间固定求最小值的操作,很容易想到用线段树维护;
具体实现方法:
- 初始化
-
使用线段树查询区间
-
状态转移
这里的
#include 四. 单调队列优化
类比数据结构优化,单调队列优化的特征为区间不固定(滑动窗口),队列头部在保证合法的状态下,是现在的最优决策,在尾部将每次更新的决策插入,同时维护队列的单调性;
适用范围:1D/1D动态规划
所谓1D/1D动态规划,即状态转移方程形如
的动态规划;
对于纯单调队列的优化,其中
单调队列优化的基本思路:
对于一个状态
依据这个思路,我们来分析一下时间复杂度:
假设现在
朴素:枚举一次
单调队列优化:每个
例题
首先很容易想出一个状态
很容易想出状态转移方程:
其中,
可以用滚动数组将第一位滚掉以满足内存需求;
时间复杂度:
不妨从状态设计下手,发现时间段的范围很小,所以可以重定义状态
状态转移方程:
发现时间复杂度
不难发现,对于一个相同的时间段,移动的方向是固定的,且随着
具体实现操作:
-
分情况确定移动的方向;
-
在此方向维护一个单调队列存相应的决策
-
队头即为最优决策,用队头更新当前状态;
-
将当前状态作为决策从队尾插入,同时维护单调性;
注意: 单调队列中维护的是决策(即状态转移方程中的
第一维可以用滚动数组滚掉;
具体实现请看代码:
#include 不难发现,在单调队列优化时,我们通常将状态看做常量,将决策看做变量,每次保证决策的单调性,是做这部分题的小技巧;
推荐一道题
五. 斜率优化
刚刚我们探讨了单调队列优化的基本操作,让我们回顾一下1D/1D动态规划的状态转移方程:
我们知道,当
如果有乘积项,就需要用到斜率优化;
当出现乘积项时,我们很容易联想到平面直角坐标系中形如
斜率优化的主要思想:及时排除无用决策;
接下来,我们依据例题来解释斜率优化;
例题
首先求出
定义
时间复杂度:
考虑优化;
不妨设题目中
不难发现,状态的第二维(批次)是一个附加状态,即它不是求答案的直接手段,只是求答案的一个附加手段;
考虑优化掉这一维;
其实当我们在执行一批任务时,并不是关心它之前机器启动了多少次,而是应该关心机器的启动对现在状态所耽误的时间;
如果不知道之前机器启动了多少次,怎么去求机器的启动对现在状态所耽误的时间?
我们可以换一个角度思考,机器因执行一批任务所花费的启动时间
依据上述思路,我们定义
值得注意的是,在费用提前计算的思想下,只有目标
时间复杂度:
还是不行,再次考虑优化;
发现这个优化过的状态转移方程满足1D/1D的动态规划,且
将方程展开,得到:
因为在平面直角坐标系中,纵坐标是随横坐标变化的,所以我们去掉
在以
这也就是说,我们的决策其实也就对应这个平面直角坐标系中的一个个点,这条直线就对应着我们现在的状态,要用决策去更新状态,需要让这条线去撞决策点;

如图所示;
现在我们想要让
现在我们来考虑一个点能成为最优决策的条件,并依此排除无用决策;

如图,发现当这三个点构成一个“上凸”形时,点

如图,发现当这三个点构成一个“下凸”形时,这三个点都可能成为最优决策;
发现:一个决策点
这里有个技巧,当我们求斜率时,最好保证两边都为正数,以省去不必要的计算与变号
当取等号时,
于是,我们只需用单调队列维护一个下凸壳(如第二张图)即可,其中斜率单调递增;
当我们找最优决策时,可以发现最优决策点与左边点的连线斜率比
所以,总的操作为:
-
检查队首斜率与直线斜率
-
此时,队首即为最优决策,更新现在的状态;
-
依据
在进行第三步时,我们将
时间复杂度优化到了
到这,实现的代码为:
#include 但我们讨论的都是
很显然,我们上述过程中的第一步就不对了,那也没有关系,此时问题是队首不一定是最优决策,所以我们不能弹出队首,而必须维护整个凸壳,依据决策斜率的单调性,每次二分查找满足上述过程中的第一步并更新即可;
队尾操作不变;
时间复杂度:
#include 推荐题目
斜率优化一般会结合前缀和,在求解斜率时,可以化除为乘,但不易查错。也可以将斜率写为函数,但容易丢精度;
六. 四边形不等式优化
四边形不等式定义:
其中
定理
对于形如
的状态转移方程,设
在状态转移方程
中,若函数
显然,在
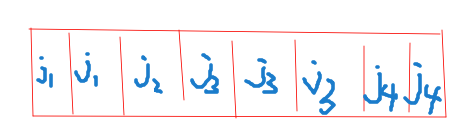
这显示了
维护一个三元组
用单调队列维护
- 检查队头,设队头三元组为
设队尾三元组为
-
若对于
-
否则,在队尾二分查找,找到一个位置,使得在这个位置及右边
-
将三元组
结语
概括来讲,
-
有可随意划分的,用倍增优化;
-
发现环形,破环成链,或者复制一倍在末尾,用环形处理的思路;
-
状态转移的方向与
-
状态转移方程需要在定区间内查询最值等等,用数据结构优化;
-
1D/1D的动态规划,需要维护动态区间,当
-
当
总之,