编译原理-词法分析器

对于词法分析器的要求

概念

• 词法分析的任务：从左到右逐个字符地对源程序进行扫描，产生一个个单词符号
• 词法分析器：又称扫描器，执行词法分析的程序

词法分析器的功能和输出形式

• 功能：输入源程序，输出单词符号
• 关键字：程序语言定义的具有固定意义的标识符，例如Pascal中的begin、end、if、while
• 标识符：表示各种名字：如变量名、数组名和过程名
• 常数：整型、实型、布尔型、文字型。
• 运算符：+、-、*、/
• 界符：逗号、分号、括号
• 输出的单词符号：（单词种别， 单词符号的属性值）
  • 单词种别：单词种别通常用符号编码表示
    
• 词法分析器在编译器中的地位
  

词法分析器的设计

词法分析器的结构

• 输入缓冲区:输入源程序文本，输入串放在一个缓冲区中,
• 扫描缓冲区：
  
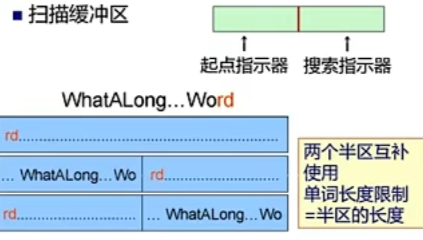
• 预处理子程序主要的工作:剔除无用的空白、空格、换行、回车等字符
• 扫描器：处理经过预处理子程序处理过的相对规整的字符串

单词符号的识别：超前搜索

• 关键字的识别：
  
• 标识符的识别：字母开头的字母数字串，后跟界符或算符
• 常数识别：识别出算术常数并将其转变为二进制内码表示，有些也要超前搜索
• 算符和界符的识别：把多个字符结合而成的算符和界符拼合成一个单一单词符合
• 几点限制-不必使用超前搜索：
  1.所有关键字都是保留字
  2.关键字作为特殊的标识符处理，都是用保留字表
  3.如果基本字、标识符、常量之间没有确定的运算符或界符做间隔，则必须使用一个空白符做间隔

状态转换图

• 节点：代表状态，用圆圈表示
  
• 箭弧：状态之间用箭弧连接，箭弧上的标记代表射出结状态下可能出现的输入字符或字符类
  有限个状态必须有初态和终态
• 状态转换图可用于识别一定的字符串：若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于alfa，则称alfa为改状态转换图所识别。
  
  

正规表达式和有限自动机

正规式和正规集

• 正规式：正规集的名字，当我们一看到正规式的时候就能想起来正规式对应的正规集
• 正规集：真正的字集，可以理解为我们要研究的程序语言单词的集合就是正规集
• 正规式等价：若两个正规式所表示的正规集相同，则认为二者等价

确定有限自动机（DFA）

确定有限自动机是状态转换图的一种形式化表示

eg：

答案：B

我们考虑转换到状态1的条件：我们只有在接收到字符a的时候才会转换成状态1，而想要从状态1转换的状态3则必须要再接收一个字符a，考虑状态2，只有在接收到字符b的情况下才会转换到状态2，然后终态一定是以aa或bb结尾吗？我们看到终态还可以接收a|b转圈，所以一定不是以aa|bb结尾，但是要想从初态到终态，一定会经过1、2两个状态中的一个，所以一定会出现连续的aa|bb

ans:A
A:识别的是空串，从初态到终态可以一个字都不接收
B:识别的是空集

非确定有限自动机（NFA）

NFA和DFA统称为有限自动机

• 定义：
  下图是DFA和NFA的状态转换图
  
  

• DFA是NFA的区别
  
  DFA和NFA的转换：子集法

1. 将初态唯一化
2. 将弧上面的多个字符集|正规式变成单个字符
   
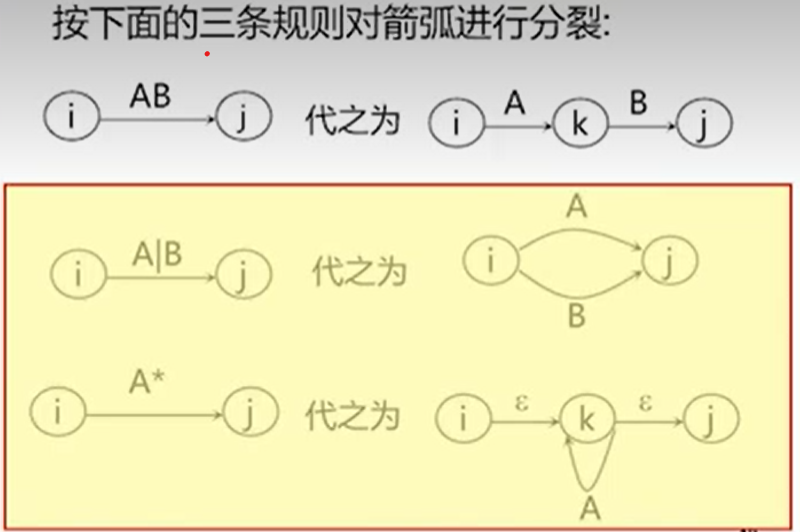
3. 将弧上的ε去掉、且做唯一化
   

这一步是将弧上的ε去掉，这样我们把这些识别字相同的状态放在一起了，这样直接放在一起还会有一个问题就是他们还有自己的识别状态

经过a弧：严格意义上经过一个a弧,强调个数,再对J做ε闭包

I 和 Ia的关系：I和Ia都是一个状态，I经过若干个弧（第一个弧是a后面的弧都是ε）可以到达Ia，实际意义就是I识别一个a字符到达Ia，
这一步进行的意义是将状态之间的转换，变为状态集之间的转换，这样就有可能消除映射不是单值部分映射的问题

正规文法与有限自动机等价

首先我们引入一个X、Y形成一个新的NFA，这个NFA只有唯一初态和终态

将X、Y之间按这样的规则进行转换，直到剩下最后两个状态

例子

正规文法和有限自动机的等价性

正规文法和有限自动机等价的定义：正规文法产生的语言和有限自动机能识别的字的集合相同即对于正规文法G和有限自动机M，如果L(G)=L(M)，则成G和M是等价的
对于正规文法和有限自动机等价有如下结论：

1. 对于每一个右线性文法G或左线性文法G，都存在一个有限自动机（FA）M，使得L（G）= L（M）
2. 对于任意一个有限自动机（FA）M，都存在一个右线性文法G或左线性文法G，使得L（G）= L（M）
   一个将右线性文法转化为FA的例子
   
   一个左线性文法转化为FA的例子