LetCode刷题[简单题](1)刷手续费

入门的动态规划的题目

状态转移类方程类似现代控制论中的内容

一般的动态规划题目思路三步走：

1. 定义状态转移方程
2. 给定转移方程初始值
3. 写代码递推实现转移方程

定义二维数组分别存储状态和天数

表示第 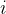天不持有可获得的最大利润；

表示第 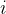天持有可获得的最大利润（注意是第 iii 天持有，而不是第 iii 天买入）

定义状态转移方程：

不持有：

\(dp[i][0]=max(dp[i−1][0],dp[i−1][1]+prices[i]−fee)\)

持有：

\(dp[i][1]=max(dp[i−1][1],dp[i−1][0]−prices[i])dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])dp[i][1]=max(dp[i−1][1],dp[i−1][0]−prices[i])\)

对于第 0天：

• 不持有：与前一个相比。
• 持有：也是一直与前一个相比。

最后总都迭代出最大

int maxProfit(vector<int>& prices, int fee) {
    int n = prices.size(); // 获取股票价格数组的长度
    if (n == 0) {
        return 0; // 如果数组为空，返回0，因为没有交易可以进行
    }
 
    int buy = -prices[0];  // 初始化持有股票的最大利润为第一天的股票价格的相反数
    int sell = 0;         // 初始化不持有股票的最大利润为0
 
    for (int i = 1; i < n; i++) {
        int prev_buy = buy; // 存储上一轮持有股票的最大利润
        buy = max(buy, sell - prices[i]); // 计算当前持有股票的最大利润，可以选择继续持有或者卖出之前的股票
        sell = max(sell, prev_buy + prices[i] - fee); // 计算当前不持有股票的最大利润，可以选择继续不持有或者买入股票
    }
 
    return sell; // 返回最终不持有股票时的最大利润，这个值就是答案
}

解答思路1：

1.针对输入

对于输入的价格首先要获取输入的长度

2.输入代码鲁棒性处理

针对输入的是否为空则提前终止代码

3.初始化最大利润，与不持有的最大利润，通过迭代方式获得最大利润

直接遍历每次都返回买的结果，相当于跟随时间进行遍历，然后计算得到最大值。

这段C++代码的时间复杂度是 O(n)，其中 n 是股票价格数组的长度。这是因为代码中使用了一个循环来遍历整个股票价格数组，每次循环都只涉及常数时间的操作。

空间复杂度是 O(1)，即常数空间。这是因为代码中只使用了常数个额外变量来存储状态，例如 buy、sell、prev_buy 和 n，它们的数量不随输入数据规模增加而变化。因此，这个算法的空间复杂度是恒定的，与输入数据规模无关。

解答思路2：

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size(); // 获取股票价格数组的长度
        int sell = 0, buy = -prices[0]; // 初始化不持有股票时的最大利润为0，初始化持有股票时的最大利润为第一天的股票价格的相反数
 
        for (int i = 1; i < n; ++i) { // 从第二天开始遍历股票价格数组
            // 计算在当前情况下，如果卖出或者继续持有股票，哪一种方式可以获得更大的利润
            // max(sell, buy + prices[i] - fee) 表示在当前价格下卖出股票并扣除手续费的情况
            // max(buy, sell - prices[i]) 表示在当前价格下继续持有股票的情况
            tie(sell, buy) = pair(max(sell, buy + prices[i] - fee), max(buy, sell - prices[i]));
        }
        return sell; // 返回最终不持有股票时的最大利润，即问题的答案
    }
};

在这段代码中，tie 是一个C++标准库中的函数，用于将多个变量绑定在一起。它的作用是在一行代码中同时更新多个变量的值。在这里，tie 的目的是同时更新 sell 和 buy 这两个变量。

具体地，tie(sell, buy) 将 sell 和 buy 这两个变量绑定在一起，然后通过 pair 函数的返回值来同时更新它们的值。pair 函数的返回值是一个包含两个值的pair（一种键-值对的数据结构），它的第一个值是 max(sell, buy + prices[i] - fee)，第二个值是 max(buy, sell - prices[i])。

通过这种方式，一行代码同时更新了 sell 和 buy 的值，避免了需要编写两行代码分别更新它们的情况。这种技巧可以提高代码的可读性和简洁性。在这里，它用于在每次循环迭代中更新股票交易的状态