图像处理与计算机视觉--第五章-图像分割-霍夫变换

1.霍夫变换(Hough Transform)原理介绍

 Hough Transform是一种常用的计算机视觉图形检验方法，霍夫变换一般用于检验直线或者圆。

 霍夫变换的原理具体如下所示:
 假设图像中存在一条直线，表达式如下所示：
$$y=kx+b$$
 假设我们任意指定一个点$(x_0,y_0)$，则对于任意穿过该点的直线，一定有如下公式成立:
$$b=-k{x}_0+y_0$$
 此时我将以x,y为轴的图像变为以b,k为轴的图像,此时该直线也能够进行变化，并且如上推导可知，对应的图像也是一条直线，如图所示:

 进一步的,我们再从直线上取一点$(x_1,y_1)$，则必有如下公式：
$$b=-k{x}_1+y_1$$
 在图像上绘制会这样的函数，我们可知，两条直线相交于一点$(k^{\ast },b^{\ast })$，而这个点就是x,y轴上的$(x_1,y_1)$和$(x_0,y_0)$两点所确定的直线。

 但是我们在实际的直线检测中，我们不会用到上述的坐标系方法，上述的方法只是提供一个求解的思路，我们将使用极坐标方程来完成上述方法的求解,对于上述的直线，极坐标方程可以表示为:
$$\rho =xcos\theta +sin\theta$$
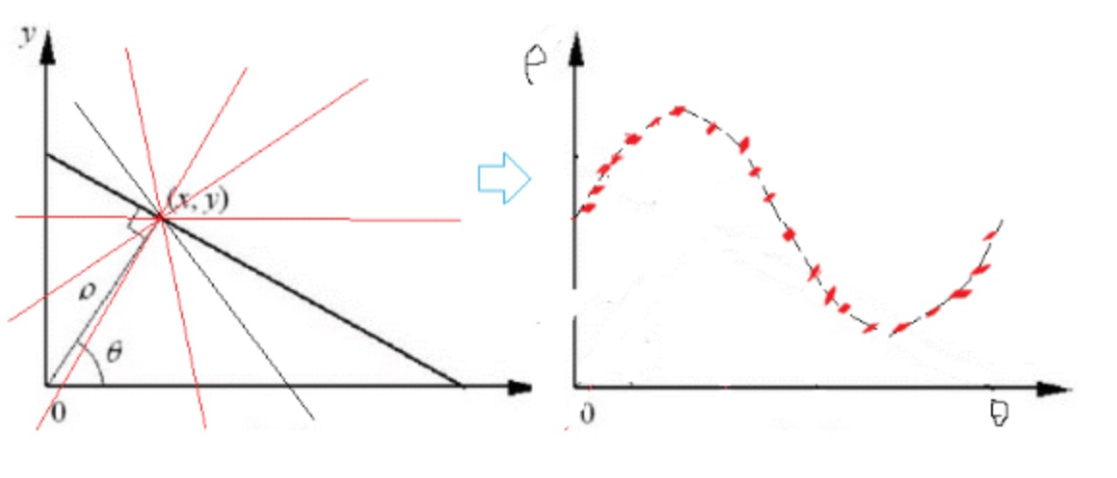
 其中，$\theta$为直线的法线向量与x轴正向的夹角，而$\rho$为坐标系原点至直线的垂直距离,如下图所示:

 如下所示，我们可以发现，这条直线在极坐标下只有一个($\rho$,$\theta$) 与之对应，改变一个参数大小变换到空域上的直线即会改变。而空域这条直线上的所有点都可以在极坐标为($\rho$,$\theta$) 所表示的直线上 (如下图所示)

 空域直线上的一个点在极坐标系下具体对应多少个极坐标对，取决于$\theta$的步长 ，如果设步长为$\beta$,则极坐标对n的表示如下所示：
$$n=\frac{360}{\beta }$$
 对应的图片如下所示:

 接下来我们假设空域上的三个点对应的极坐标曲线如下图的(a)所示，极坐标曲线同时经过一个点表示空域下有一条直线经过这三个点，只要寻找交点最多的点，在空域内就是要寻找的直线。

2.霍夫变换(Hough Transform)算法流程

·Hough变换直线检测的步骤如下:
1.设0的取值范围为[0,360]，单位为度根据检测精度要求，采取适当的步长对角度和长度的取值范围进行离散化，形成0-p平面上的离散网格。
2.将每一个离散网格视为一个投票累加器，初始时全部清0。
3.遍历图像的所有像素，对于每个像素计算离散值0i和p=xcos0+ysin0.
4.对在参数空间中将对应的累加器中的值加1，从而完成求出相应的离散化值p，对于每个(p,0)该像素点的投票的投票之后，在离散化的参数空间中找出所累积的投票值
5.访问完所有的图像像素并完成所有，点这些点所对应的参数即为检测得到的直线的参数大于某给定闽值T的局部极大值点，
1
2
3
4
5
6

3.霍夫变换(Hough Transform)算法代码

import numpy as np
import cv2
from PIL import Image,ImageEnhance 
import matplotlib.pyplot as plt
"""
hough变换是一种常用的计算机视觉图形检验方法，霍夫变换一般用于检验直线或者圆。

"""
img = Image.open(r"C:\Users\Zeng Zhong Yan\Desktop\py.vs\python学习\test.webp")
#增强图像效果
img = ImageEnhance.Contrast(img).enhance(3)
img.show()
#处理成矩阵，便于后续处理
img = np.array(img)
#灰度处理
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#cv2.THRESH_OTSU具有双峰值，显示效果更好.
"""
cv2.THRESH_OTSU使用最小二乘法处理像素点。一般情况下,cv2.THRESH_OTSU适合双峰图。
cv2.THRESH_TRIANGLE使用三角算法处理像素点。一般情况下,cv2.THRESH_TRIANGLE适合单峰图。
"""
ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU)
#canny边缘检验算法处理
result = cv2.Canny(thresh, ret-30, ret+30, apertureSize=3)

#霍夫变换检测直线
lines = cv2.HoughLinesP(result, 1, 1 * np.pi / 180, 10, minLineLength=10, maxLineGap=5)
# 画出检测的线段
for line in lines:
    for x1, y1, x2, y2 in line:
        cv2.line(img, (x1, y1), (x2, y2), (255, 0, 0),2)
img = Image.fromarray(img, 'RGB')
img.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

4.霍夫变换(Hough Transform)算法效果

1.原先的图片如下所示:

2.霍夫变换后的检测直线的效果