图论算法＜三＞：Dijkstra算法介绍及分析

1、介绍

  迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

  Dijkstra是用来求单源最短路径的，即从一个顶点出发，只能求一个顶点到其他点的最短距离而不能任意两点。Dijkstra处理带权值的具体实例更多一些。比如一个城市有多个乡镇，乡镇可能有道路，也可能没有，整个乡镇联通，如果想计算每个乡镇到ａ镇的最短路径，那么Dijkstra就派上了用场。

2、算法分析

  Dijkstra算法的前提条件和环境：一个连通图，若干节点，节点可能有数值，但是路径一定有权值。并且路径不能为负。

  Dijkstra的核心思想是贪心算法的思想。贪心算法（又称贪婪算法）指在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

2.1 算法前提

  首先，Dijkstra处理的是带正权值的有权图，那么，就需要一个二维数组（如果空间大用list数组）存储各个点到达(边)的权值大小(邻接矩阵或者邻接表存储)。
  其次，还需要一个boolean数组判断那些点已经确定最短长度，那些点没有确定。int数组记录距离(在算法执行过程可能被多次更新)。
  需要优先队列加入已经确定点的周围点。每次抛出确定最短路径的那个并且确定最短，直到所有点路径确定最短为止。

2.1 算法流程

  一般从选定点开始抛入优先队列。（路径一般为0），boolean数组标记0的位置(最短为0) , 然后0周围连通的点抛入优先队列中（可能是node类），并把各个点的距离记录到对应数组内(如果小于就更新，大于就不动，初始第一次是无穷肯定会更新)，第一次就结束了。
  从队列中抛出距离最近的那个点B（第一次就是0周围邻居）。这个点距离一定是最近的（所有权值都是正的，点的距离只能越来越长。）标记这个点为true，并且将这个点的邻居加入队列(下一次确定的最短点在前面未确定和这个点邻居中产生),并更新通过B点计算各个位置的长度，如果小于则更新！

3、算法示例

  问题描述： 如下无向图， 若从顶点1开始计算到其余各顶点的最短路径。

1）首先需要3个辅助数组：

• dist[] : 记录从顶点1开始到其余各顶点的最短路径

• visited[] : 记录该顶点是否被访问过， 初始值设为0

• path[] : 记录该顶点最短路径的前驱顶点

2）求最短路径步骤：

1. 初始化数组：计算从顶点0到其余各顶点的路径长度

2. 由于dist数组中目前最小值为顶点2，计算从顶点2到其余各顶点的距离， 若小于当前dist数组中的值，则更新dist和path数组；若大于当前dist数组的值， 则不做改变。

3.选择dist数组中未被访问过的最小值顶点7， 同上。

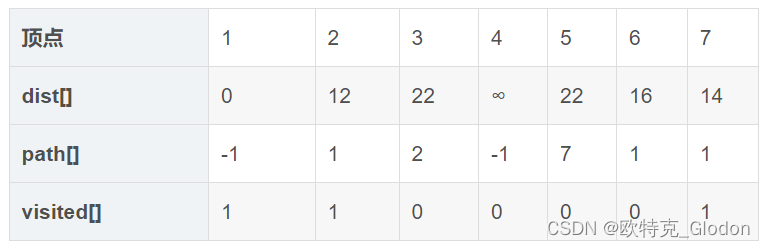
4.选择dist数组中未被访问过的最小值顶点6。

5.选择dist数组中未被访问过的最小值顶点5。

6.选择dist数组中未被访问过的最小值顶点3或者4都可以， 如选择3。

7.选择dist数组最后一个顶点4。

到这里为止， visited数组元素全为1， 即所有顶点都被访问过， 最短路径见如上图。整理后为：

v1到v1： 路径长度=0，路径：1-1。
v1到v2： 路径长度=12，路径：1-2。
v1到v3： 路径长度=22，路径：1-2-3。
v1到v4： 路径长度=22，路径：1-6-5-4。
v1到v5： 路径长度=18，路径：1-6-5。
v1到v6： 路径长度=16，路径：1-6。
v1到v7： 路径长度=14，路径：1-7。
1
2
3
4
5
6
7