栈与队列经典题目——用栈实现队列

上篇文章对栈和队列的一个经典题目——Leetcode.225-用队列实现栈进行讲解。本篇文章将对另一个题目Leetcode.232-用栈实现队列进行讲解

1. Leetcode.232——用栈实现队列：

题目如下：

1.1 大体思路分析：

题目要求需要实现下列函数所表示的功能，即：（创建队列），（用栈实现队列尾插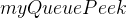），（返回队列的开头元素），（移除、返回队列开头元素），（探空），myQueueFree（释放问题解决过程中开辟的空间）。

对于上述给出需要实现的功能中，较为重要的是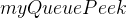：（返回队列的开头元素），（移除、返回队列开头元素），在本部分，将介绍这两种功能的实现思路。

对于栈，可以看作只能在尾部进行插入删除的线性表，对于队列，是尾部进行插入，头部进行删除的线性表。下面给出一个包含若干元素的栈，即：

题目要求用两个栈来实现队列，则，将上述栈中的元素插入到另一个栈后，及：

此时，栈的尾部存储的元素为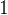，按照栈的规则，尾部插入元素，尾部删除元素，则可以达到上述给出的函数（移除、返回队列开头元素）所对应的移除开头元素的功能。对于返回队列开头元素，只需要在移除元素之前，单独创建一个变量用于存储元素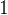，移除元素，最后返回用于存储元素的变量即可。

在利用队列实现栈的题目中，需要一个结构体指针指向一个保持为空的队列，令一个结构体指针指向的队列 用于插入元素。通过上面给出思路可知，本题需要的两个栈，一个用来接受插入的元素，将这个栈定义为，另一个栈需要接受的栈顶元素，并在之后通过出栈顶元素来实现队列关于头元素的各项功能。

1.2 功能实现：

1.2.1 栈的创建及初始化：

初始化的过程与上篇文章的中初始化原理相同，不过多赘述，只给出代码：
 

typedef struct {
    ST pushst;
    ST Popst;
} MyQueue;
 
 
MyQueue* myQueueCreate() {
    MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
    STInit(&obj->pushst);
    STInit(&obj->Popst);
   
    return obj;
  
}

1.2.2 通过栈顶插入元素 myQueuePush：

虽然栈与队列在删除元素时由一定不同，但是在插入元素时，队列是在队尾插入，栈是在栈顶，即同样是队尾插入，所以，直接调用函数，向队尾位置插入元素即可，代码如下：
 

void myQueuePush(MyQueue* obj, int x) {
    STPush(&obj->pushst,x); 
}

1.2.3 返回队列的开头元素myQueuePeek：

上面给出了实现本功能的大体思路。但是需要区分下面两种情况，即：栈中为空、栈中已经存在元素。对于前一种情况，需要将中的所有元素都插入到，最后取栈顶元素返回即可。对于后一种情况，直接取栈顶元素返回即可。

对应代码如下：
 

int myQueuePeek(MyQueue* obj) {
    if( STEmpty(&obj->Popst))
    {
        while(!STEmpty(&obj->pushst))
        {
            STPush(&obj->Popst,STTop(&obj->pushst));
            STPop(&obj->pushst);
        }
    }
    return STTop(&obj->Popst);
}

1.2.3 从队头删除并返回队头元素：

上个功能中，已经实现了返回栈顶元素，所以在实现本功能时，只需要创建一个变量用于存储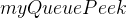的返回值，再移除栈顶元素，最后返回即可。对应代码如下：

int myQueuePop(MyQueue* obj) {
    int front = myQueuePeek(obj);
    STPop(&obj->Popst);
    return front; 
}

1.2.4 探空：

原理较为简单，只给出代码，不做多余解释：

bool myQueueEmpty(MyQueue* obj) {
    return STEmpty(&obj->Popst) && STEmpty(&obj->pushst);
}

1.2.5 释放解决问题所开辟的空间myQueueFree：

同样，只给出代码，不做多余解释：

void myQueueFree(MyQueue* obj) {
    STDestory(&obj->pushst);
    STDestory(&obj->Popst);
 
    free(obj);
 
}

2. 结果及代码总览：

2.1 运行结果：

2.2 代码总览：

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;
 
//栈的初始化：
void STInit( ST* ps )
{
	assert(ps);
 
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}
 
//栈的销毁：
void STDestory(ST* ps)
{
	assert(ps);
 
	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}
 
void STPush(ST* ps, STDataType x)
{
	assert(ps);
	
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? ps->capacity = 4: ps->capacity * 2;
		STDataType* newnode = (STDataType*)realloc(ps->a,sizeof(STDataType) * newcapacity);
		if (newnode == NULL)
		{
			perror("realloc");
		}
		ps->a = newnode;
		ps->capacity = newcapacity;
	}
 
	ps->a[ps->top] = x;
	ps->top++;
}
 
void STPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
 
	ps->top--;
 
}
 
int size(ST* ps)
{
	assert(ps);
 
	return ps->top;
}
 
bool STEmpty(ST* ps)
{
	assert(ps);
 
	return ps->top == 0;
}
 
STDataType STTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
 
	return ps->a[ps->top-1];
 
}
 
 
 
//栈的初始化：
void STInit(ST* ps);
 
//栈的销毁
void STDestory(ST* ps);
 
//通过栈顶向栈中插入元素
void STPush(ST* ps, STDataType x);
 
//删除栈中的元素：
void STPop(ST* ps);
 
//记录size
int size(ST* ps);
 
//找空
bool STEmpty(ST* ps);
 
//获取栈顶元素
STDataType STTop(ST* ps);
 
 
typedef struct {
    ST pushst;
    ST Popst;
} MyQueue;
 
 
MyQueue* myQueueCreate() {
    MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
    STInit(&obj->pushst);
    STInit(&obj->Popst);
   
    return obj;
  
}
 
void myQueuePush(MyQueue* obj, int x) {
    STPush(&obj->pushst,x); 
}
 
int myQueuePeek(MyQueue* obj) {
    if( STEmpty(&obj->Popst))
    {
        while(!STEmpty(&obj->pushst))
        {
            STPush(&obj->Popst,STTop(&obj->pushst));
            STPop(&obj->pushst);
        }
    }
    return STTop(&obj->Popst);
}
 
int myQueuePop(MyQueue* obj) {
    int front = myQueuePeek(obj);
    STPop(&obj->Popst);
    return front; 
}
 
bool myQueueEmpty(MyQueue* obj) {
    return STEmpty(&obj->Popst) && STEmpty(&obj->pushst);
}
 
void myQueueFree(MyQueue* obj) {
    STDestory(&obj->pushst);
    STDestory(&obj->Popst);
 
    free(obj);
 
}