LeetCode每日一题(2201. Count Artifacts That Can Be Extracted)

There is an n x n 0-indexed grid with some artifacts buried in it. You are given the integer n and a 0-indexed 2D integer array artifacts describing the positions of the rectangular artifacts where artifacts[i] = [r1i, c1i, r2i, c2i] denotes that the ith artifact is buried in the subgrid where:

• (r1i, c1i) is the coordinate of the top-left cell of the ith artifact and
• (r2i, c2i) is the coordinate of the bottom-right cell of the ith artifact.
  You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.

Given a 0-indexed 2D integer array dig where dig[i] = [ri, ci] indicates that you will excavate the cell (ri, ci), return the number of artifacts that you can extract.

The test cases are generated such that:

• No two artifacts overlap.
• Each artifact only covers at most 4 cells.
• The entries of dig are unique.

Example 1:

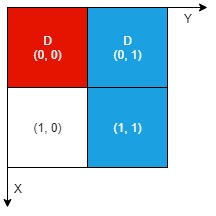
Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
Output: 1

Explanation:
The different colors represent different artifacts. Excavated cells are labeled with a ‘D’ in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.

Example 2:

Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
Output: 2

Explanation: Both the red and blue artifacts have all parts uncovered (labeled with a ‘D’) and can be extracted, so we return 2.

Constraints:

• 1 <= n <= 1000
• 1 <= artifacts.length, dig.length <= min(n2, 105)
• artifacts[i].length == 4
• dig[i].length == 2
• 0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1
• r1i <= r2i
• c1i <= c2i
• No two artifacts will overlap.
• The number of cells covered by an artifact is at most 4.
• The entries of dig are unique.

---

没想到什么简单办法， 就是把 grid 根据 artifacts 画出来， grid[row][col] = i, i 为 artifacts 的 index, 同时创建一个 counts 来统计同一 artifact 所覆盖的 cell 的数量， 然后我们遍历 dig， 根据挖开的 grid 中的 i, 去 counts 中做相应的减除， 如果 counts[i] == 0 了， 那我们就可以认为 artifacts[i]所覆盖的所有 cell 都被挖开了。

---

impl Solution {
    pub fn dig_artifacts(n: i32, artifacts: Vec<Vec<i32>>, dig: Vec<Vec<i32>>) -> i32 {
        let mut grid = vec![vec![-1; n as usize]; n as usize];
        let mut counts = vec![0; artifacts.len()];
        for (i, art) in artifacts.into_iter().enumerate() {
            for r in art[0]..=art[2] {
                for c in art[1]..=art[3] {
                    grid[r as usize][c as usize] = i as i32;
                    counts[i] += 1;
                }
            }
        }
        let mut ans = 0;
        for d in dig {
            let i = grid[d[0] as usize][d[1] as usize];
            if i >= 0 {
                counts[i as usize] -= 1;
                if counts[i as usize] == 0 {
                    ans += 1;
                }
            }
        }
        ans
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25