wy的leetcode刷题记录_Day43

wy的leetcode刷题记录_Day40

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2022-11-15

前言

今天时间比较多而且题目比较简单，应该能写三四道题。

1710. 卡车上的最大单元数

今天的每日一题是：1710. 卡车上的最大单元数

题目介绍

请你将一些箱子装在 一辆卡车 上。给你一个二维数组 boxTypes ，其中 boxTypes[i] = [numberOfBoxesi, numberOfUnitsPerBoxi] ：

• numberOfBoxesi 是类型 i 的箱子的数量。
• numberOfUnitsPerBoxi 是类型 i 每个箱子可以装载的单元数量。

整数 truckSize 表示卡车上可以装载 箱子 的 最大数量 。只要箱子数量不超过 truckSize ，你就可以选择任意箱子装到卡车上。

返回卡车可以装载 单元 的 最大 总数。

示例 1：
输入：boxTypes = [[1,3],[2,2],[3,1]], truckSize = 4
输出：8
解释：箱子的情况如下：

• 1 个第一类的箱子，里面含 3 个单元。
• 2 个第二类的箱子，每个里面含 2 个单元。
• 3 个第三类的箱子，每个里面含 1 个单元。 可以选择第一类和第二类的所有箱子，以及第三类的一个箱子。 单元总数 = (1 * 3) + (2 * 2) + (1 * 1) = 8

示例 2：
输入：boxTypes = [[5,10],[2,5],[4,7],[3,9]], truckSize = 10
输出：91

思路

方法一：一个简单的贪心思路：先将boxTypes按照其numberOfUnitsPerBoxi的大小排列顺序，然后根据其数量装箱，到最后只有俩种情况，就是该类型的箱子数量>剩下所需的箱子数量，这样的话只需把剩下所需的箱子数量的该类型的箱子放入即可；还有就是该类型的箱子数量<剩下所需的箱子数量，这样就需要将该类型的箱子全部放入后，继续放入下一个类型的箱子。
方法二：由于本题目的数据量较小，所以可以创建一个空的数组truck，通过遍历boxTypes，填充这个数组，下标为其箱子能装载的单元数量，值为箱子的数量。最后从后往前再遍历这个truck，也就是从最大的箱子能装载的单元数量开始放入。（这样的话相比于方法一的排序时间复杂度要低一些的）

代码

贪心：

class Solution {
public:
    int maximumUnits(vector<vector<int>>& boxTypes, int truckSize) {
        //
        int ans=0;
        if(boxTypes.empty())
            return ans;
        sort(boxTypes.begin(), boxTypes.end(), [](const vector<int> &a, const vector<int> &b) {
            return a[1] > b[1];
        });
        int j=0;
        for(auto boxType:boxTypes)
        {
            int box_num=boxType[0];
            int box_val=boxType[1];
            
            if(box_num<=truckSize)
            {
                ans+=box_num*box_val;
                truckSize-=box_num;
            }

            else
            {
                ans+=truckSize*box_val;
                break;
            }


        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

计数排序：

class Solution {
public:
    int maximumUnits(vector<vector<int>>& boxTypes, int truckSize) {
        int truck[1001] = {0};
        for (auto& boxType : boxTypes) {
            int numberOfBoxesi  = boxType[0], numberOfUnitsPerBoxi  = boxType[1];
            truck[numberOfUnitsPerBoxi ] += numberOfBoxesi ;
        }
        int ans = 0;
        for (int numberOfUnitsPerBoxi = 1000; numberOfUnitsPerBoxi > 0 && truckSize > 0; --numberOfUnitsPerBoxi) {
            int numberOfBoxesi = truck[numberOfUnitsPerBoxi];
            if (numberOfBoxesi) {
                ans += numberOfUnitsPerBoxi * min(truckSize, numberOfBoxesi);
                truckSize -= numberOfBoxesi;
            }
        }
        return ans;
    }
};



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

收获

简单的模拟贪心思路，以及再数据量小的时候可以稍微牺牲一下空间性能来提升时间性能

513. 找树左下角的值

513. 找树左下角的值

题目介绍

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

输入: root = [2,1,3]
输出: 1

示例 2:

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

思路

方法一：DFS：前序遍历，维护一个最大深度和最大深度左节点值就可以
方法二：BFS：记录层次，遍历到最深层次后第一个值就是树左下角的值

代码

DFS:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    public:
        int maxLen = INT_MIN;
        int maxleftValue;
        void traversal(TreeNode* root, int leftLen) 
        {
            if (root->left == NULL && root->right == NULL) 
            {
                if (leftLen > maxLen) 
                {
                    maxLen = leftLen;
                    maxleftValue = root->val;
                }
                return;
            }
            if (root->left)
             {
                traversal(root->left, leftLen + 1); // 隐藏着回溯
            }
            if (root->right) 
            {
                traversal(root->right, leftLen + 1); // 隐藏着回溯
            }
            return;
            }

        int findBottomLeftValue(TreeNode* root) {
            traversal(root, 0);
            return maxleftValue;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

BFS:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        int ans=0;
        queue<TreeNode*> qu;
        if(!root)
            return ans;
        qu.push(root);
        while(!qu.empty())
        {
            int n=qu.size();
            for(int i=0;i<n;i++)
            {
                TreeNode* node=qu.front();
                qu.pop();
                if(i==0)
                    ans=node->val;
                if(node->left)
                    qu.push(node->left);
                if(node->right)
                    qu.push(node->right);
            }
        }
        return ans;
    }

};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

收获

熟练了BFS和DFS对各种要求的应用

112. 路径总和

112. 路径总和

题目介绍

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

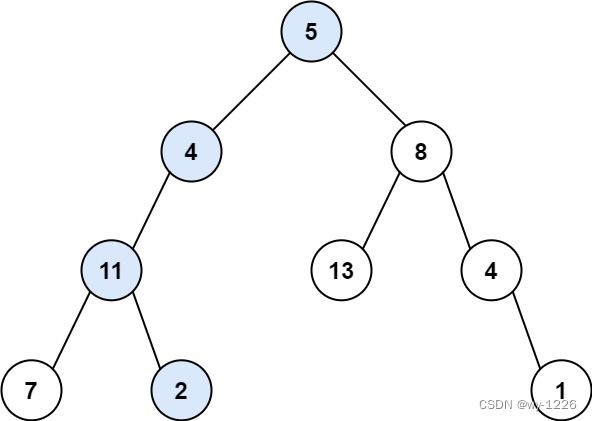
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：

• (1 -->2): 和为 3
• (1 --> 3): 和为 4

不存在 sum = 5 的根节点到叶子节点的路径。

思路

本题方法太多了，我这里只写了一个用栈来模拟递归的方法。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(!root)
            return false;
        stack<pair<TreeNode *,int>> path;
        path.push({root,root->val});
        
        while(!path.empty())
        {
            pair<TreeNode *,int> node=path.top();
            path.pop();
            if (!node.first->left && !node.first->right && targetSum == node.second) 
                return true;
            if (node.first->left) {
                path.push(pair<TreeNode*, int>(node.first->left, node.second +
                node.first->left->val));
            }
            // 右节点，压进去⼀个节点的时候，将该节点的路径数值也记录下来
            if (node.first->right) {
                path.push(pair<TreeNode*, int>(node.first->right, node.second +
                node.first->right->val));
            }
        }
        return false;
        }
    
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

收获

对调用系统栈的方式更加了解。

113. 路径总和 II

113. 路径总和 II

题目介绍

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

思路

BFS：这一题使用BFS还是有一些麻烦的，因为当你遍历到符合要求的叶子节点时，你需要去找到他的链路，就是根据他的父节点依次向上寻找，于是我额外使用了一个hashmap来记录每个节点的父节点。
DFS：用一个临时path来记录当前遍历的路径，并且在不符合条件回退时path也要进行回溯。

代码

BFS：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> ans;
    unordered_map<TreeNode* ,TreeNode*> parent;
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {

        if(!root)
            return ans;
        queue<pair<TreeNode*,int>> qu;
        qu.push({root,root->val});
        while(!qu.empty())
        {
            pair<TreeNode*,int> node=qu.front();
            qu.pop();
            if(!node.first->left&&!node.first->right&&node.second==targetSum)
                getPath(node.first);
            else
           {
                if(node.first->left)
                {
                    parent[node.first->left]=node.first;
                    qu.push({node.first->left,node.second+node.first->left->val});
                }

                if(node.first->right)
                {
                    parent[node.first->right]=node.first;
                    qu.push({node.first->right,node.second+node.first->right->val});
                }            
            }
        }
        return ans;
    }

    void getPath(TreeNode* node) {
        vector<int> tmp;
        while (node != nullptr) {
            tmp.emplace_back(node->val);
            node = parent[node];
        }
        reverse(tmp.begin(), tmp.end());
        ans.emplace_back(tmp);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

DFS：

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;

    void dfs(TreeNode* root, int targetSum) {
        if (root == nullptr) {
            return;
        }
        path.emplace_back(root->val);
        targetSum -= root->val;
        if (root->left == nullptr && root->right == nullptr && targetSum == 0) {
            ret.emplace_back(path);
        }
        dfs(root->left, targetSum);
        dfs(root->right, targetSum);
        path.pop_back();
    }

    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        dfs(root, targetSum);
        return ret;
    }
};


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

收获

其实这俩道题已经有较明显的回溯意思了，稍微掌握了一些。