• 二叉树的学习

    目录

    一、二叉树的基本概念

    二、二叉树的性质

    （一）二叉树的性质

    （二）完全二叉树的常考性质 

    三、二叉树的存储结构 

    （一）二叉树的顺序存储

    （二）二叉树的链式存储结构

    四、二叉树的遍历

    五、基本操作 

    （一）建立二叉链表的3种方法

    （二）先序（递归）、中序（递归）、后序（递归）、层次遍历

    （三）先序（非递归）、中序（非递归）、后序（非递归）

    （三）完整代码

    一、二叉树的基本概念

    • 二叉树是n（n>=0）个结点的有限集合

    1.或者为空二叉树，即n=0。
    2.或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一颗二叉树。
    特点：1.每个结点至多只有两棵子树。2.左右子树不能颠倒（二叉树是有序树）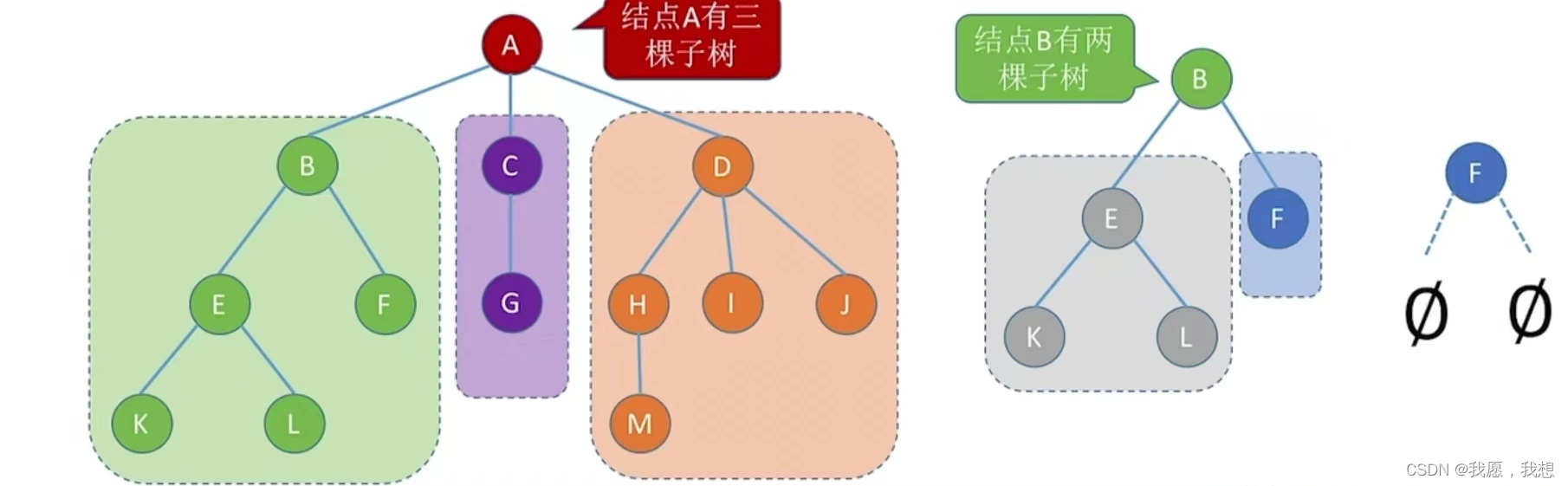 

    •  二叉树的五种状态：

     

      

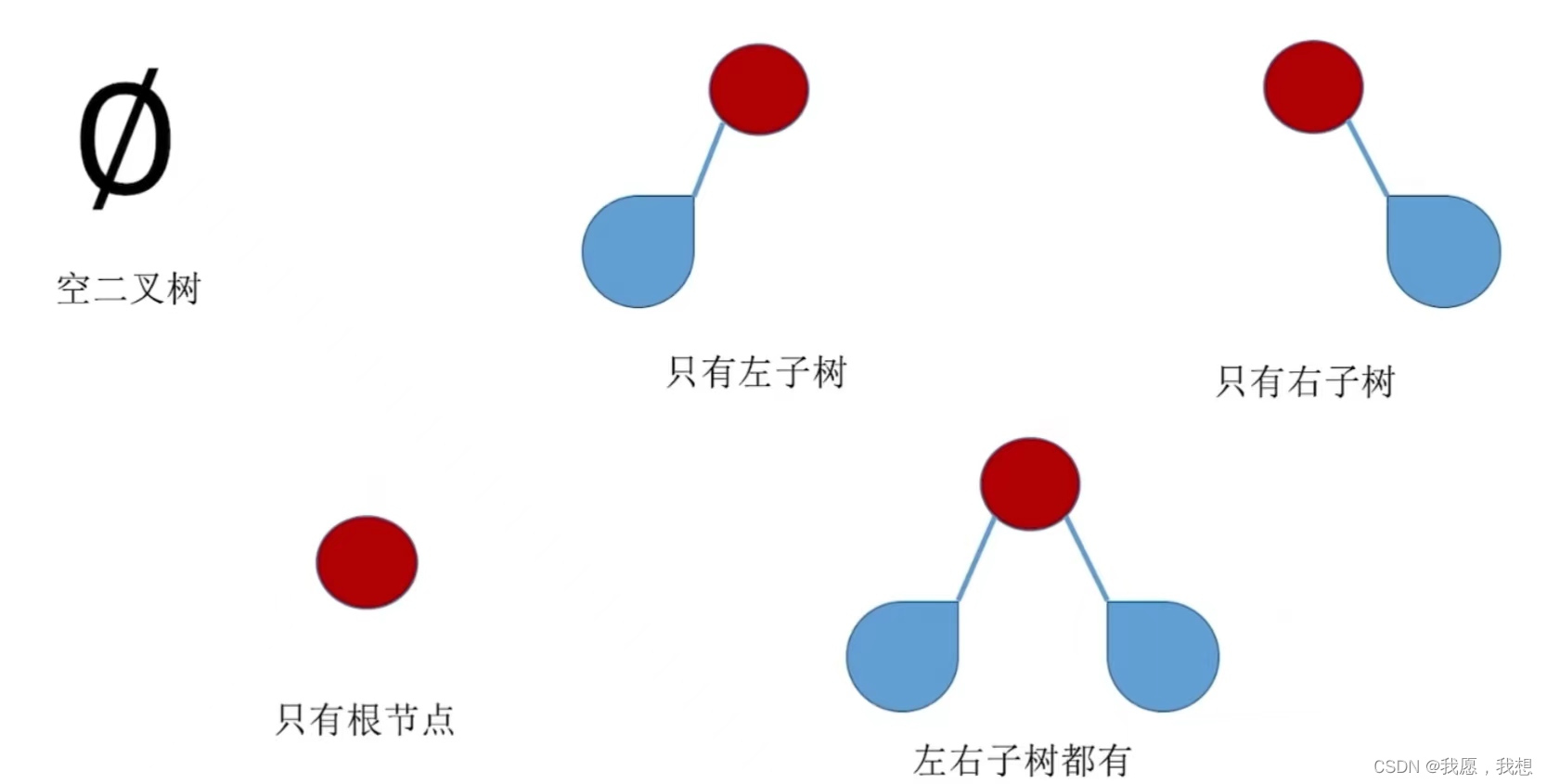
    • 满二叉树：一棵高度为h，且含有2^h-1个结点的二叉树。
    • 特点：

     

    1.只有最后一层有叶子结点。
    2.不存在度为1的结点（结点的度要么为2，要么就是0）。
    3.按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1；结点i的父结点为[i/2]（i/2然后舍去小数取整）（如果有的话） 

    • 完全二叉树：当且仅当其每个结点都与高度为h的满二叉树中编号为1到n的结点一一对应时，称为完全二叉树。
    • 特点：

    1.只有最后两层可能有叶子结点。
    2.最多只有一个度为1的结点。
    3.按层序从1开始编号，结点i的左孩子为2i，右孩子为2i + 1；结点i的父结点为[i / 2]（i / 2然后舍去小数取整）（如果有的话）
    完全二叉树：当且仅当其每个结点都与高度为h的满二叉树中编号为1到n的结点一一对应时，称为完全二叉树。
    4.当i<=[n/2]（取n/2的整数部分）为分支结点，i>[n/2]为叶子结点。 

    • 二叉排序树：一棵二叉树或者空二叉树，或者是具有如下性质的二叉树

    1.左子树上所有结点的关键字均小于根结点的关键字
    2.右子树上所有结点的关键字均大于根结点的关键字
    3.左子树和右子树又各是一棵二叉排序树
    补充：二叉排序树可用于元素的排序、搜索 

    • 平衡二叉树：树上任一结点的左子树和右子树的深度之差不超过1 

    二、二叉树的性质

    （一）二叉树的性质

    • 考点1：设非空二叉树中度为0、1和2的结点个数分别为n0，n1和n2，则n0 = n2 + 1（叶子结点比二分支结点多一个）

    分析：假设树中结点总数为n，则
    1.n = n0 + n1 + n2（树的结点数 = 度为0的结点数 + 度为1的结点数 + 度为2的结点数）
    2.n = n1 + 2n2 + 1（树的结点数 = 总度数 + 1，其中度为0的结点数有n0个，度数和为0×n0；度为1的结点数有n1个，度数和为n1；度为2的结点数有n2个，度数和为2n2。所以总度数为n1 + 2n2）
    由上面两式相等得到：n0 + n1 + n2 = n1 + 2n2 + 1，所以n0 = n2 + 1 

    • 考点2：二叉树第i层至多有2 ^ (i - 1)个结点（i >= 1）
    • 考点3：高度为h的二叉树至多有2 ^ h - 1个结点（满二叉树）

    分析：第一层有1个结点；第二层有2个结点；第三层有2^2个结点.....第h层有2^(h-1)个结点
    总共有1+2+2^2......+2^(h-1)=(1-2^h)/(1-2)=2^h-1 

    （二）完全二叉树的常考性质 

    • 考点1：具有n个（n>0）结点的完全二叉树的高度为h为[log2(n+1)]（2的底）或[log2n]+1（2是底）

    分析：

    • 考点2：对于完全二叉树，可以由结点数推出度为0、1和2的结点个数为n0、n1和n2

    分析：
    完全二叉树最多只有一个度为1的结点，即n1=0或1
    由于n0=n2+1，所以n0+n2=2n2+1一定是奇数
    又推出若完全二叉树有2k个（偶数）个结点，则必有n1=1，n0=k，n2=k-1
    若完全二叉树有2k-1个（奇数）个结点，则必有n1=0，n0=k，n2=k-1 

    三、二叉树的存储结构 

    （一）二叉树的顺序存储

    • 存储完全二叉树：

    按照一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素 

    完全二叉树结点i的的左孩子是2i，右孩子是2i+1，父结点是[i/2]（i/2后取整），所在层次是[log2(n+1)]（2为底） 

    • 不是完全二叉树的顺序存储需要增加空结点

     

    • 顺序存储结构 
    1. //第一种
    2. typedef struct wqbtree
    3. {
    4.     ElemType SBTree[MaxSize];//结点中的数据元素
    5.     int n;//记录结点个数
    6. }Fbitree;
    7.  
    8. //第二种
    9. typedef ElemType SBTree[MaxSize];

    （二）二叉树的链式存储结构

    二叉树中每一个结点用链表中的一个结点来存储，结构结点如上图。 

    其中data表示值域，用于存储对应的数据元素；lchild和rchild分别表示左指针域和右指针域 ，分别用于存储左孩子结点和右孩子结点的地址。

    • 链式存储结构
    1. typedef struct BTNode
    2. {
    3.     ElemType data;//数据域
    4.     struct BTNode* lchild, * rchild;//左右孩子指针
    5. }BTNode,*BTree;

    四、二叉树的遍历

    • 二叉树的递归特性：

          1.要么是个空二叉树
          2.要么就是由“根结点+左子树+右子树”组成的二叉树 

    • 二叉树的遍历是指按照一定的次序访问树中的所有结点，并且每个结点仅被访问一次的过程。
    • 常见的4中递归遍历方法：

      1.先序遍历（DLR）
      第一步：访问根结点；第二步先序遍历左子树；第三步：先序遍历右子树。
      2.中序遍历（LDR）
      第一步：中序遍历左子树；第二步：访问根节点；第三步：中序遍历右子树。
      3.后序遍历（LRD）
      第一步：后序遍历左子树；第二步：后序遍历右子树；第三步：访问根结点。
      4.层序遍历
      第一步：访问根结点（第一层）
      第二步：从左到右访问第2层所有结点。
      第三步：从左到右访问第3层所有结点、....、第h层所有结点。 

    五、基本操作 

    （一）建立二叉链表的3种方法

    1. BTree Creat(char str[])//先序序列建立二叉链表（方法1）
    2. {
    3.     BTree T;
    4.     static int i = 0;
    5.     ElemType c = str[i++];
    6.     if (c == '#')//输入#表示此结点下不存在分支
    7.     {
    8.         T = NULL;
    9.     }
    10.     else
    11.     {
    12.         T = (BTree)malloc(sizeof(BTree));
    13.         if (T == NULL)
    14.         {
    15.             exit(0);
    16.         }
    17.         T->data = c;
    18.         T->lchild = Creat(str);//递归创建左子树
    19.         T->rchild = Creat(str);//到上一个结点的右边递归创建左右子树
    20.     }
    21.     return T;
    22. }
    23.  
    24. void CreateBT(BTree& T) // 先序遍历建立二叉链表 （方法2）
    25. {
    26.     ElemType ch;
    27.     cin >> ch;
    28.     if (ch == '^')
    29.         T = NULL;
    30.     else
    31.     {
    32.         T = (BTNode*)malloc(sizeof(BTNode));
    33.         T->data = ch;
    34.         cout << "请输入" << ch << "的左子树：";
    35.         CreateBT(T->lchild);
    36.         cout << "请输入" << ch << "的右子树：";
    37.         CreateBT(T->rchild);
    38.     }
    39. }
    40.  
    41. void CreatBTNode(BTree& T, char* str)//（方法3）
    42. {
    43.     BTNode* st[MAXSIZE];
    44.     BTNode* p = NULL;
    45.     int top = -1, k, j = 0;
    46.     ElemType ch;
    47.     ch = str[j];
    48.     while (ch != '\0')//str未扫描完的时候循环
    49.     {
    50.         switch (ch)
    51.         {
    52.         case '('://为左孩子结点
    53.             top++;
    54.             st[top] = p;
    55.             k = 1;
    56.             break;
    57.         case ')':
    58.             top--;
    59.             break;
    60.         case ','://为右孩子结点
    61.             k = 2;
    62.             break;
    63.         default:
    64.             p = (BTree)malloc(sizeof(BTree));
    65.             p->data = ch;
    66.             p->lchild = p->rchild = NULL;
    67.             if (T == NULL)//p结点第一次创建
    68.             {
    69.                 T = p;
    70.             }
    71.             else
    72.             {
    73.                 switch (k)
    74.                 {
    75.                 case 1:
    76.                     st[top]->lchild = p;//p结点为栈顶结点的左孩子
    77.                     break;
    78.                 case 2:
    79.                     st[top]->rchild = p;//p结点为栈顶结点的右孩子
    80.                     break;
    81.  
    82.                 }
    83.             }
    84.  
    85.         }
    86.         ch = str[++j];//继续扫描下一个字符
    87.     }
    88. }

    方法3解释：例如A（B（D（，G）），C（E，F）） 

    （二）先序（递归）、中序（递归）、后序（递归）、层次遍历

    • 层次遍历算法思想：遍历从二叉树的根结点开始，首先将根结点入队列，然后进行下面的操作

    1.取出队头元素
    2.访问该元素所指结点
    3.若该元素所指结点的左、右孩子结点非空，则将该元素所指结点的左孩子和右孩子指针入队
    4.若队列非空，重复1-3；当队列为空的时候，二叉树的层次遍历结束。 

    1. void PreOrder(BTree T)//先序遍历
    2. {
    3.     if (T != NULL)
    4.     {
    5.         cout << T->data << " ";//访问根结点
    6.         PreOrder(T->lchild);//先序遍历左子树
    7.         PreOrder(T->rchild);//先序遍历右子树
    8.     }
    9. }
    10.  
    11. void InOrder(BTree T)//中序遍历
    12. {
    13.     if (T != NULL)
    14.     {
    15.         InOrder(T->lchild);
    16.         cout << T->data << " ";
    17.         InOrder(T->rchild);
    18.     }
    19.  
    20. }
    21. void PostOrder(BTree T)//后序遍历
    22. {
    23.     if (T != NULL)
    24.     {
    25.         PostOrder(T->lchild);
    26.         PostOrder(T->rchild);
    27.         cout << T->data << " ";
    28.     }
    29. }
    30.  
    31.  
    32. void LevelOrder(BTree T)//层序遍历
    33. {
    34.     BTNode* p;
    35.     BTNode* qu[MAXSIZE];//定义循环队列，存放结点指针
    36.     int front, rear;//定义头指针和尾指针
    37.     front = rear=0;//置队列为空队列
    38.     rear++;//根结点指针进队
    39.     qu[rear] = T;
    40.     while (front != rear)//队列不为空
    41.     {
    42.         front = (front + 1) % MAXSIZE;//队头指针加1取模
    43.         p = qu[front];//队头结点出队
    44.         cout << p->data << " ";
    45.         if (p->lchild != NULL)
    46.         {
    47.             rear = (rear + 1) % MAXSIZE;//队尾指针加1取模
    48.             qu[rear] = p->lchild;//p结点的左孩子进栈
    49.         }
    50.         if (p->rchild != NULL)
    51.         {
    52.             rear = (rear + 1) % MAXSIZE;
    53.             qu[rear] = p->rchild;//p结点的右孩子进栈
    54.         }
    55.     }
    56. }

    （三）先序（非递归）、中序（非递归）、后序（非递归）

    • 先序遍历的关键：在先序遍历某个结点的整个左子树后，如何找到该结点的右子树的根指针？解决方法：在访问完该结点后，将该结点的指针保存在栈中，以便以后能通过它找到该结点的右子树。

    • 中序遍历：采用一个栈保存需要回溯的结点地址，先扫描（并非访问根结点）的所有左下结点并将它们一一进栈，然后出栈一个结点，该结点一定没有左孩子结点或者左子树已遍历过，则访问它；然后转向该结点的右孩子结点（如果有），将其进栈，再遍历该右孩子结点的所有左下结点并一一进栈；如此循环，直到栈空并且遍历指针p空为空。

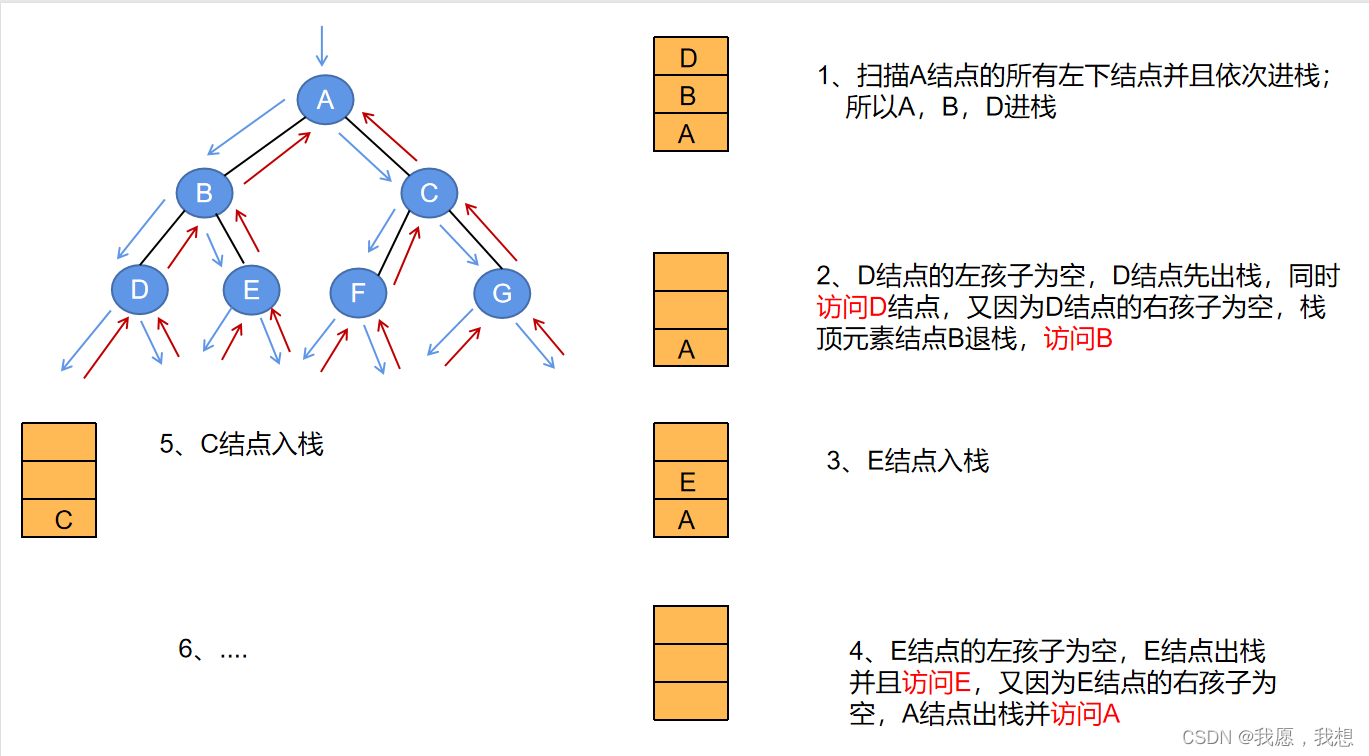
    • 后序遍历：采用一个栈保存需要回溯的结点地址，先扫描根结点的所有左下结点并且一一进栈。将栈顶结点T作为当前结点，如果结点T可以访问，则访问它；否则转向结点T的右子树遍历其右子树。 
    1. bool FirstOrder(BTree T)//先序遍历非递归算法
    2. {
    3.     BTNode* st[MAXSIZE];//st数组存放栈元素
    4.     // BTNode* st[MAXSIZE]因为[]的优先级比*高，所以st先与[]结合，形成数组，再与*结合，
    5.     //所以这个数组的类型BTNode*，就是指向BTNode的指针，就是“元素是指向BTNode型数据的指针的数组”。
    6.     // 每个元素都是一个指针，一共有MAXSIZE个元素
    7.     int top = -1;//top为栈顶指针
    8.     BTNode* p = T;
    9.     while (p != NULL || top != -1)//当前结点不为空或者栈不为空
    10.     {
    11.         while (p != NULL)//当前结点不为空
    12.         {
    13.             cout << p->data << " ";
    14.             top++;
    15.             st[top] = p;//当前结点入栈
    16.             p = p->lchild;//左孩子作为当前结点
    17.         }
    18.         if (top != -1)//当栈不为空
    19.         {
    20.             p = st[top];//将栈顶元素赋值给p
    21.             top--;//栈顶元素出栈
    22.             p = p->rchild;//指向栈顶元素的右孩子
    23.         }
    24.     }
    25.     return true;
    26. }
    27.  
    28.  
    29. bool InOrder2(BTree T)//中序遍历非递归算法
    30. {
    31.     BTNode* st[MAXSIZE];//st数组存放栈元素
    32.     int top = -1;
    33.     BTNode* p = T;
    34.     while (p != NULL || top != -1)
    35.     {
    36.         while (p != NULL)
    37.         {
    38.             top++;
    39.             st[top] = p;
    40.             p = p->lchild;
    41.         }
    42.         if (top != -1)
    43.         {
    44.             p = st[top];//获取栈顶结点
    45.             cout << p->data << " ";
    46.             top--;//栈顶结点出栈
    47.             p = p->rchild;//指向栈顶结点的右孩子
    48.         }
    49.     }
    50.     return true;
    51. }
    52.  
    53. void PostOrder2(BTree T)//后序遍历非递归算法
    54. {
    55.     BTNode* st[MAXSIZE];
    56.     BTNode* p ;
    57.     int flag = -1;
    58.     int top = -1;
    59.  
    60.     do{
    61.         while (T != NULL)
    62.         {
    63.             top++;
    64.             st[top] = T;
    65.             T = T->lchild;
    66.         }
    67.         p = NULL;
    68.         flag = 1;//表示栈顶的结点的左孩子被处理过
    69.         while (top != -1 && flag == 1)//对栈顶结点进行连续判断
    70.         {
    71.             T = st[top];
    72.             if (T->rchild == p)
    73.             {
    74.                 cout << T->data << " ";
    75.                 top--;
    76.                 p = T;
    77.             }
    78.             else
    79.             {
    80.                 T = T->rchild;
    81.                 flag = 0;//表示当前结点的左孩子没有被处理过
    82.             }
    83.  
    84.         }
    85.  
    86.      }while (top != -1);
    87.     cout << endl;
    88. }

    （三）完整代码

    1. #include
    2. #include
    3. #include
    4. using namespace std;
    5. #define MAXSIZE 100
    6. typedef char ElemType;
    7. typedef struct BTNode
    8. {
    9.     ElemType data;//数据域
    10.     struct BTNode* lchild, * rchild;//左右孩子指针
    11. }BTNode, * BTree; 
    12. BTree Creat(char str[]);//先序序列建立二叉链表（方法1）
    13. void CreateBT(BTree& T); // 先序遍历建立二叉链表（方法2）
    14. void CreatBTNode(BTree& T, char* str);//利用ch扫描，采用括号表示法表示的二叉树字符串（方法3）
    15.  
    16. void PreOrder(BTree T);//先序遍历
    17. void InOrder(BTree T);//中序遍历
    18. void PostOrder(BTree T);//后序遍历
    19. void LevelOrder(BTree T);//层序遍历
    20.  
    21. //非递归算法
    22. bool FirstOrder(BTree T);//先序遍历非递归算法
    23. bool InOrder2(BTree T);//中序遍历非递归算法
    24. void PostOrder2(BTree T);//后序遍历非递归算法
    1. //#include"TreeNode.h"
    2.  
    3. BTree Creat(char str[])//先序序列建立二叉链表（方法1）
    4. {
    5.     BTree T;
    6.     static int i = 0;
    7.     ElemType c = str[i++];
    8.     if (c == '#')//输入#表示此结点下不存在分支
    9.     {
    10.         T = NULL;
    11.     }
    12.     else
    13.     {
    14.         T = (BTree)malloc(sizeof(BTree));
    15.         if (T == NULL)
    16.         {
    17.             exit(0);
    18.         }
    19.         T->data = c;
    20.         T->lchild = Creat(str);//递归创建左子树
    21.         T->rchild = Creat(str);//到上一个结点的右边递归创建左右子树
    22.     }
    23.     return T;
    24. }
    25.  
    26. void CreateBT(BTree& T) // 先序遍历建立二叉链表 （方法2）
    27. {
    28.     ElemType ch;
    29.     cin >> ch;
    30.     if (ch == '^')
    31.         T = NULL;
    32.     else
    33.     {
    34.         T = (BTNode*)malloc(sizeof(BTNode));
    35.         T->data = ch;
    36.         cout << "请输入" << ch << "的左子树：";
    37.         CreateBT(T->lchild);
    38.         cout << "请输入" << ch << "的右子树：";
    39.         CreateBT(T->rchild);
    40.     }
    41. }
    42.  
    43. void CreatBTNode(BTree& T, char* str)//（方法3）
    44. {
    45.     BTNode* st[MAXSIZE];
    46.     BTNode* p = NULL;
    47.     int top = -1, k, j = 0;
    48.     ElemType ch;
    49.     ch = str[j];
    50.     while (ch != '\0')//str未扫描完的时候循环
    51.     {
    52.         switch (ch)
    53.         {
    54.         case '('://为左孩子结点
    55.             top++;
    56.             st[top] = p;
    57.             k = 1;
    58.             break;
    59.         case ')':
    60.             top--;
    61.             break;
    62.         case ','://为右孩子结点
    63.             k = 2;
    64.             break;
    65.         default:
    66.             p = (BTree)malloc(sizeof(BTree));
    67.             p->data = ch;
    68.             p->lchild = p->rchild = NULL;
    69.             if (T == NULL)//p结点第一次创建
    70.             {
    71.                 T = p;
    72.             }
    73.             else
    74.             {
    75.                 switch (k)
    76.                 {
    77.                 case 1:
    78.                     st[top]->lchild = p;//p结点为栈顶结点的左孩子
    79.                     break;
    80.                 case 2:
    81.                     st[top]->rchild = p;//p结点为栈顶结点的右孩子
    82.                     break;
    83.  
    84.                 }
    85.             }
    86.  
    87.         }
    88.         ch = str[++j];//继续扫描下一个字符
    89.     }
    90. }
    91.  
    92.  
    93.  
    94. void PreOrder(BTree T)//先序遍历
    95. {
    96.     if (T != NULL)
    97.     {
    98.         cout << T->data << " ";//访问根结点
    99.         PreOrder(T->lchild);//先序遍历左子树
    100.         PreOrder(T->rchild);//先序遍历右子树
    101.     }
    102. }
    103.  
    104. void InOrder(BTree T)//中序遍历
    105. {
    106.     if (T != NULL)
    107.     {
    108.         InOrder(T->lchild);
    109.         cout << T->data << " ";
    110.         InOrder(T->rchild);
    111.     }
    112.  
    113. }
    114. void PostOrder(BTree T)//后序遍历
    115. {
    116.     if (T != NULL)
    117.     {
    118.         PostOrder(T->lchild);
    119.         PostOrder(T->rchild);
    120.         cout << T->data << " ";
    121.     }
    122. }
    123.  
    124.  
    125. void LevelOrder(BTree T)//层序遍历
    126. {
    127.     BTNode* p;
    128.     BTNode* qu[MAXSIZE];//定义循环队列，存放结点指针
    129.     int front, rear;//定义头指针和尾指针
    130.     front = rear = 0;//置队列为空队列
    131.     rear++;
    132.     qu[rear] = T;//根结点指针进队
    133.     rear++;//队尾指针指向队尾元素的后一个位置
    134.     front = (front + 1) % MAXSIZE;//队头指针加1取模
    135.     while (front != rear)//队列不为空
    136.     {
    137.         p = qu[front];//取队头元素
    138.         front = (front + 1) % MAXSIZE;//队头元素出队，队头指针后移
    139.         cout << p->data << " ";
    140.         if (p->lchild != NULL)
    141.         {
    142.             qu[rear] = p->lchild;//p结点的左孩子进栈
    143.             rear = (rear + 1) % MAXSIZE;//队尾指针加1取模
    144.         }
    145.         if (p->rchild != NULL)
    146.         {
    147.             qu[rear] = p->rchild;//p结点的右孩子进栈
    148.             rear = (rear + 1) % MAXSIZE;
    149.         }
    150.     }
    151. }
    152.  
    153.  
    154.  
    155.  
    156.  
    157. bool FirstOrder(BTree T)//先序遍历非递归算法
    158. {
    159.     BTNode* st[MAXSIZE];//st数组存放栈元素
    160.     // BTNode* st[MAXSIZE]因为[]的优先级比*高，所以st先与[]结合，形成数组，再与*结合，
    161.     //所以这个数组的类型BTNode*，就是指向BTNode的指针，就是“元素是指向BTNode型数据的指针的数组”。
    162.     // 每个元素都是一个指针，一共有MAXSIZE个元素
    163.     int top = -1;//top为栈顶指针
    164.     BTNode* p = T;
    165.     while (p != NULL || top != -1)//当前结点不为空或者栈不为空
    166.     {
    167.         while (p != NULL)//当前结点不为空
    168.         {
    169.             cout << p->data << " ";
    170.             top++;
    171.             st[top] = p;//当前结点入栈
    172.             p = p->lchild;//左孩子作为当前结点
    173.         }
    174.         if (top != -1)//当栈不为空
    175.         {
    176.             p = st[top];//将栈顶元素赋值给p
    177.             top--;//栈顶元素出栈
    178.             p = p->rchild;//指向栈顶元素的右孩子
    179.         }
    180.     }
    181.     return true;
    182. }
    183.  
    184.  
    185. bool InOrder2(BTree T)//中序遍历非递归算法
    186. {
    187.     BTNode* st[MAXSIZE];//st数组存放栈元素
    188.     int top = -1;
    189.     BTNode* p = T;
    190.     while (p != NULL || top != -1)
    191.     {
    192.         while (p != NULL)
    193.         {
    194.             top++;
    195.             st[top] = p;
    196.             p = p->lchild;
    197.         }
    198.         if (top != -1)
    199.         {
    200.             p = st[top];//获取栈顶结点
    201.             cout << p->data << " ";
    202.             top--;//栈顶结点出栈
    203.             p = p->rchild;//指向栈顶结点的右孩子
    204.         }
    205.     }
    206.     return true;
    207. }
    208.  
    209. void PostOrder2(BTree T)//后序遍历非递归算法
    210. {
    211.     BTNode* st[MAXSIZE];
    212.     BTNode* p ;
    213.     int flag = -1;
    214.     int top = -1;
    215.  
    216.     do{
    217.         while (T != NULL)
    218.         {
    219.             top++;
    220.             st[top] = T;
    221.             T = T->lchild;
    222.         }
    223.         p = NULL;
    224.         flag = 1;//表示栈顶的结点的左孩子被处理过
    225.         while (top != -1 && flag == 1)//对栈顶结点进行连续判断
    226.         {
    227.             T = st[top];
    228.             if (T->rchild == p)
    229.             {
    230.                 cout << T->data << " ";
    231.                 top--;
    232.                 p = T;
    233.             }
    234.             else
    235.             {
    236.                 T = T->rchild;
    237.                 flag = 0;//表示当前结点的左孩子没有被处理过
    238.             }
    239.  
    240.         }
    241.  
    242.      }while (top != -1);
    243.     cout << endl;
    244. }
    1. //#include"TreeNode.h"
    2. int main()
    3. {
    4. 	cout << "二叉树建立的第一种方法" << endl;
    5. 	BTree T;//T为指向根结点的指针
    6. 	T=(BTree)malloc(sizeof(BTree));
    7. 	char str[] = { 'a','b','d','#','#','e','#','#','c','f','#','#','g','#','#' };
    8. 	T = Creat(str);
    9. 	cout << "先序遍历结果：";
    10. 	PreOrder(T);//先序遍历
    11. 	cout << endl;
    12. 	cout << "中序遍历结果：";
    13. 	InOrder(T);//中序遍历
    14. 	cout << endl;
    15. 	cout << "后序遍历结果：";
    16. 	PostOrder(T);//后序遍历
    17. 	cout << endl ;
    18. 	cout << "层次遍历的结果：";
    19. 	LevelOrder(T);
    20. 	cout << endl<
    21.  
    22. 	cout << "（非递归）先序遍历结果：";
    23. 	FirstOrder(T);//先序遍历非递归算法
    24. 	cout << endl;
    25. 	cout << "（非递归）中序遍历结果：";
    26. 	InOrder2(T);//中序遍历非递归算法
    27. 	cout << endl;
    28. 	cout << "（非递归）后序遍历结果：";
    29. 	PostOrder2(T);
    30. 	cout << endl;
    31.  
    32. 	cout << "二叉树建立的第二种方法" << endl;
    33. 	BTree T2;
    34. 	cout << "请输入第一个数据：";
    35. 	CreateBT(T2);
    36. 	cout << "先序遍历结果：";
    37. 	PreOrder(T2);
    38. 	cout << endl << endl;
    39.  
    40.  
    41. 	cout << "二叉树建立的第三种方法" << endl;
    42. 	BTree T3 = NULL;
    43. 	char s[] = "A(B(D(,G)),C(E,F))";
    44. 	CreatBTNode(T3, s);
    45. 	cout << "先序遍历结果是：";
    46. 	PreOrder(T3);//先序遍历
    47. 	cout << endl;
    48. 	cout << "（非递归）先序遍历结果是：";
    49. 	FirstOrder(T3);
    50. 	cout << endl;
    51. 	return 0;
    52. }

  • 相关阅读:
    java基于springboot+vue+elementui的 废品回收站管理系统
    java计算机毕业设计web网上办公自动化系统MyBatis+系统+LW文档+源码+调试部署
    计算机图形学实验——2023-09-28
    19种分布式系统设计模式
    微信小程序的民宿客房预订uniapp小程序
    Java 中 String、StringBuffer、StringBuilder 的用法与区别
    低照度图像数据集
    总体最小二乘法(TLS)
    猿创征文| 指针，这还拿不下你？
    组件以及组件间的通讯
  • 原文地址：https://blog.csdn.net/m0_63783532/article/details/127804395