AcWing 836. 合并集合 —— 递推递归一起食用效果更佳哦~

题目描述

---

分析：

前置知识

并查集是一种维护集合的数据结构，它的名字中的“并”“查”“集”分别取自 Union（合并），Find（查找），Set（集合）这 3 个单词。也就是说，并查集支持下面两个操作：

• 合并：合并两个集合。
• 查找：判断两个元素是否在一个集合内。

而并查集的实现是极为简洁的，只需要一个数组 ：father[N]即可。
其中 father[i] 表示元素 i 的父亲结点，而父亲结点本身也是这个集合内的元素($1\le i\le N$)。另外，如果 father[i] == i，则说明元素 i 是该集合的根结点，但对同一个集合来说只存在一个根结点，且将其作为所属集合的标识。举个例子更形象一些：

father[1] = 1 // 1 的父亲结点是自己，也就是说 1 号是根结点
father[2] = 1 // 2 的父亲结点是 1
father[3] = 2 // 3 的父亲结点是 2
father[4] = 2 // 4 的父亲结点是 2
1
2
3
4

看完了并查集的基本结构后我们来解决最开始提出的两个操作（设初始时每个元素都是独立的一个集合）。
查找： 由于规定同一个集合只存在一个根结点，因此查找操作就是对给定的结点寻找其根结点的过程。实现的方式有递推和递归两种，其思路都是一样的，即反复寻找父亲结点，直到找到根结点（即 father[i] == i 的结点）。

// 递推版本
int findFather(int x)
{
	while (x != father[x]) x = father[x]; // 直至找到根结点
	return x;
}


// 递归版本
int findFather(int x)
{
	if (x == father[x]) return x; // 若找到根结点，返回编号 x
	else return findFather(father[x]); // 否则递归判断 x 的父结点是否为根结点
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

合并： 合并两个集合的过程一般是把其中一个集合的根结点的父亲指向另一个集合的根结点。

// 为了方便理解，这里将合并操作写一个函数，但在题目中可以一步给出
// 即 father[findFather(a)] = findFather(b)
void Union(int a, int b)
{
	int fa = findFather(a);
	int fb = findFather(b);
	if (fa != fb) father[fa] = fb;
}
1
2
3
4
5
6
7
8

这里简要说明一下并查集里的一个性质。在合并的过程中，只对两个不同的集合进行合并，如果两个元素在相同的集合中就不会对其进行操作，这就保证了同一个集合中一定不会产生环，即并查集产生的每一个集合都是一棵树。

路径压缩

上面说的那个并查集的查找操作是没有经过优化的，在极端情况下效率极低，比如下面这个极端情况：

总共有 $10^5$ 个元素形成一条链，那么假设要进行 $10^5$ 次查询，且每次查询都查询最后面的结点的根结点，那么每次都要花费 $10^5$ 的计算量查找，这显然无法承受。
我们可对其进行优化，结果为：

father[1] = 1 ——> father[1] = 1
father[2] = 1 ——> father[2] = 1
father[3] = 2 ——> father[3] = 1
father[4] = 3 ——> father[4] = 1
1
2
3
4

对应的图形变化为：

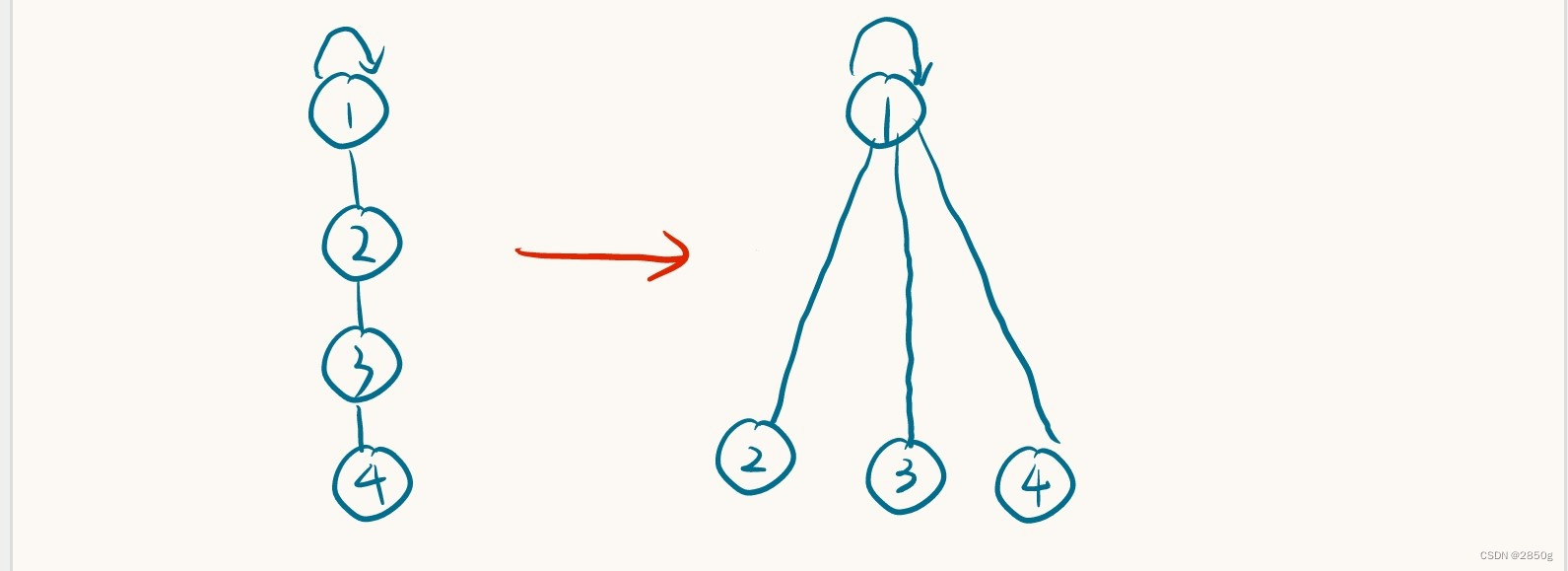
那么如何进行优化呢？我们的目标是把当前结点的路径上的所有结点的父亲都指向根结点，查找的时候就不需要一直回溯去找父亲了，可以如下考虑：

1. 按原先的写法获得 x 的根结点 F。
2. 重新从 x 开始走一遍寻找根结点的过程，把路径上经过的所有结点的父亲结点全部改为根结点 F。

代码如下：

// 递推版本
int findFather(int x)
{
	// 由于 x 在下面 while 中会变成根结点，因此先把原来的 x 保存一下
	int a = x;
	while (x != father[x]) x = father[x]; // 寻找根结点
	// 到这里，x 存放的是根结点，下面把路径上的所有结点的 father 都改为根结点
	while (a != father[a])
	{
		// 因为 a 要被 father[a] 覆盖，所以先保存号 a 的值，以修改 father[a]
		int z = a;
		a = father[a]; // a “向上”跳到父结点
		father[z] = x; // 将原先的结点 a 的父亲改为根结点
	}
	return x;
}
// 递归版本
int findFather(int x)
{
	if (x == father[x]) return x; // 找到根结点
	else
	{
		int F = findFather(father[x]); // 递归寻找 father[x] 的根结点 F
		father[x] = F;
		return F; // 返回根结点来为其他结点赋值
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

这样就可以在查找时把寻找根结点的路径压缩了。具体的数学推导这里不给出（证不出 -.- ），可以把路径压缩后的查找操作认为是一个几乎为 $O(1)$ 的操作。

---

代码(C++)

#include 

using namespace std;

const int N = 100010;
int father[N];

int findFather(int x)
{
	if (x == father[x]) return x; // 找到根结点
	else
	{
		int F = findFather(father[x]); // 递归寻找 father[x] 的根结点 F
		father[x] = F;
		return F; // 返回根结点来为其他结点赋值，进行路径压缩
	}
}

int main()
{
    int n, m;
    cin >> n >> m;
    
    // 初始化
    for (int i = 1; i <= n; i ++) father[i] = i;
    
    while (m --)
    {
        char op;
        int a, b;
        cin >> op >> a >> b;
        
        if (op == 'M') father[findFather(a)] = findFather(b);
        else
        {
            if (findFather(a) == findFather(b)) puts("Yes");
            else puts("No");
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

---