LeetCode - 数组的旋转总结

1. 数组的旋转总结

数组的旋转指的是将数组的最后若干个数提前到数组前面，数组的翻转指的是将数组的顺序颠倒。旋转可以通过多次翻转实现。

数组的翻转很简单，通过双指针来实现：交换数组的第一个数和最后一个数，交换第二个数和倒数第二个数，一直到数组中间即可。

2. 题目记录

189. 轮转数组

分析题意

给你一个数组，将数组中的元素向右轮转 k **个位置，其中 k **是非负数。

思路分析

其实题目就是一个数组旋转问题，我们可以通过图片来分析一下：

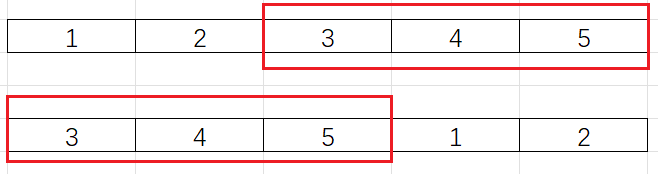
将上面这个数组向右轮转3个位置，其实就是：将数组的后3个元素旋转到数组前面，即：数组的旋转。前面我们讲到：数组的旋转可以通过多次数组翻转来实现：

我们首先对整个数组进行翻转，然后对每一个子数组进行翻转，即：数组的旋转通过三次数组的翻转来实现。

class Solution {
    public void rotate(int[] nums, int k) {
        k = k % nums.length;
        // 整个数组进行翻转
        reverse(nums, 0, nums.length - 1);
        // 前k个元素进行翻转
        reverse(nums, 0, k - 1);
        // 剩余元素进行翻转
        reverse(nums, k, nums.length - 1);

    }

    void reverse(int[] nums, int left, int right){
        int temp = 0;
        while(left < right){
            temp = nums[left];
            nums[left] = nums[right];
            nums[right] = temp;
            left ++;
            right --;
        }
    }
}

复杂度分析

时间复杂度：$O(n)$
空间复杂度：$O(1)$

396. 旋转函数

分析题意

看到题目似乎我们需要模拟旋转操作，然后求出每次旋转之后的总和，并所有旋转总和中取最大值。

但其实只求最大值的话，我们无需进行模拟。让我们来看看不同旋转操作之间的规律性：

a = (0 * 4) + (1 * 3) + (2 * 2) + (3 * 6)
b = (1 * 4) + (2 * 3) + (3 * 2) + (0 * 6)
c = (2 * 4) + (3 * 3) + (0 * 2) + (1 * 6)
d = (3 * 4) + (0 * 3) + (1 * 2) + (2 * 6)

从上面我们可以分析一下a、b、c和d之间的关系：

b = a + 4 + 3 + 2 + 6 - 4 * 6
c = b + 4 + 3 + 2 + 6 - 4 * 2
d = c + 4 + 3 + 2 + 1 - 4 * 3

每次都等于上次的和加上数组总和减去当前遍历到的元素的n倍。

思路分析

class Solution {
    public int maxRotateFunction(int[] nums) {
        int sum = 0;
        int ans = 0;
        for(int i = 0; i < nums.length; i++){
            ans = ans + i * nums[i];
            sum += nums[i];
        }

        int pre = ans;
        for(int i = nums.length - 1; i >= 0; i--){
            pre = pre + sum - nums.length * nums[i];
            ans = Math.max(ans, pre);
        }
        return ans;
    }
}

复杂度分析

时间复杂度：$O(n)$

空间复杂度：$O(1)$