• NR 物理层编码 - slide4 循环码Cyclic Code

    前言：

          线性码，循环码系列一般参考国内的教材都差不多.这边以海外的一个

    知名博主,eigen chris的《Cyclic codes-Polynomial Properties》,一种非常

    新颖的视角去阐述码多项式，我们也可以通过它去深刻理解我们的编码本质

    低纬度的空间到高纬度空间的映射，这个跟机器学习分类原理非常相似。

     vaild codeword(蓝色点,前面许可集概念一样）

    参考：  

        eigen chris的《Cyclic codes-Polynomial Properties》

       10.循环码-系统结构循环码_哔哩哔哩_bilibili

    目录 

    1.     系统结构循环码和循环码
    2.     循环码生成和监督矩阵
    3.     多项式

    一   系统结构循环码和循环码

          给定生成多项式g(x),循环码有两种形式:系统结构和非系统结构

        1： 非系统结构

                 c(x)=u(x)g(x)

        2:    系统结构

                c_s(x)=x^{n-k}u(x)+p(x)

               其中

               p(x)=mod:\frac{x^{n-k}u(x)}{g(x)}    

        例 （7,4）循环码 ,g(x)=x^3+x^2+1,u=[1100]

        求循环码,系统结构循环码

         解： u(x)=x^3+x^2

          循环码：

          c(x)=u(x)g(x)=(x^3+x^2)(x^3+x^2+1)

                                       =x^6+x^4+x^3+x^2

           系统结构循环码

           n=7,k=4,n-k=3

           I(x)=x^{n-k}u(x)=x^6+x^5

           p(x)=\frac{x^6+x^5}{x^3+x^2+1}

                        =x^2+1

             c_s(x)=I(x)+p(x)=x^6+x^5+x^2+1

    二   循环码生成和监督矩阵

        系统码多项式形式

           c_s(x)=x^{n-k}A(x)+p(x),p(x)\equiv \frac{x^{n-k}A(x)}{g(x)}

          

         则生成矩阵形式如下:

          G(x)=\begin{bmatrix} x^{n-1}+p_{k-1}(x)\\ x^{n-2}+p_{k-2}(x) \\ .... \\ x^{n-k+1}+p_{1}(x) \\ x^{n-k}+p_{0}(x) \end{bmatrix}

    设  A_i(x)=x^i,i=1,..k-1

         \frac{x^{n-k}A_i(x)}{g(x)}=Q_i(x)+\frac{P_i(x)}{g(x)}

         p_i(x)\equiv \frac{x^{n-k}A_i(x)}{g(x)}

       系统生成矩阵

     H=[P_{k,n-k}^T|I_{n-k}]

    证明：

       信息元   A(x)=a_{k-1}x^{k-1}+a_{k-2}x^{k-2}+...a_1x+a_0x^0

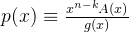
       ​​​​​​系统码多项式​c_s(x)=x^{n-k}A(x)+p(x),p(x)\equiv \frac{x^{n-k}A(x)}{g(x)}

     

       根据

       p(x) \equiv \frac{x^{n-k}A(x)}{g(x)}

               \equiv [a_{k-1},a_{k-2},...a_0]\begin{bmatrix} \frac{x^{n-k}A_{k-1}}{g(x)}\\ \frac{x^{n-k}A_{k-2}}{g(x)} \\ ... \\ \frac{x^{n-k}A_{0}}{g(x)} \end{bmatrix}

                p_i(x)=\frac{x^{n-k}A_{i}(x)}{g(x)}

       c_s(x)=a_{k-1}x^{n-k}A_{k-1}(x)+a_{k-2}x^{n-k}A_{k-2}(x)+..+a_{0}x^{n-k}A_{0}(x)+p_{k-1}(x)+p_{k-2}(x)+...+p_0(x)

                     =\begin{bmatrix} a_{k-1} &a_{k-2} &... & a_0 \end{bmatrix}\begin{bmatrix} x^{n-k}A_{k-1}(x)+p_{k-1}(x)\\ x^{n-k}A_{k-2}(x)+p_{k-2}(x) \\ .... \\ x^{n-k}A_{0}(x)+p_{0}(x) \end{bmatrix}

     例： g(x)=x^3+x^2+1的系统循环码（7,4）生成矩阵和监督矩阵H

    解：

          n=7,k=4,n-k=3

         \frac{x^{n-k}A_i(x)}{g(x)}=Q(x)+\frac{p_i(x)}{g(x)} i \in [k-1,k-2,..0]

         \left\{\begin{matrix} p_0(x)\equiv \frac{x^3}{g(x)}=x^2+1\\ p_1(x)\equiv \frac{x^4}{g(x)}=x^2+x+1\\ p_2(x)\equiv \frac{x^5}{g(x)}=x+1 \\ p_3(x)\equiv \frac{x^6}{g(x)}=x^2+x \end{matrix}\right. （除号结果为取模运算）

        

      P=\begin{bmatrix} 110\\ 011 \\ 111 \\ 101 \end{bmatrix}

     G=[I_k,P]

     

      H=[P^T,I__{n-k}]" role="presentation" style="position: relative;">H=[P^T,I__{n-k}]

     =\begin{bmatrix} 1 & 0 &1 & 1& 1 & & \\ 1 & 1& 1& 0 & & 1& \\ 0 & 1 & 1& 1& & & 1 \end{bmatrix}

    三 多项式

      eigen chris 有篇关于多项式的文章,写得非常新颖。

    编码的本质是低维空间到高维空间的映射，在高维空间

    码集分为vaild, not valid两类

     循环码也是一样,如下是多项式的形式

    比如k=1的bit,经过repetion 码

    如左图，收到10,01那肯定就发生错误了。

    右图 通过生成多项式g(x)=1+x ，可以认为在维度[1,x]上面的投影

    发现收到的码字为x,1肯定发送了错误.

     余数的解释

  • 相关阅读:
    uniapp使用sqlite
    百度智能云正式上线Python SDK版本并全面开源！
    QT学习管理系统
    JavaScript作用域实战
    InputMan12.0J、VB.net、imTime
    docker容器内调用宿主机docker执行
    网络安全（黑客）自学
    d.ts你知道多少？
    write tcp 127.0.0.1:53226-＞127.0.0.1:6379: use of closed network connection
    让我十二点催她睡觉，我用 Python 轻松解决
  • 原文地址：https://blog.csdn.net/chengxf2/article/details/126894831