软考中级-软件设计师-第2章计算机组成与体系结构

1 数据的表示

1.1 进制转换

1.2 机器编码方式

1.3 浮点数的表示

因为担心新增内容无法及时保存，导致编辑的内容丢失，所以多次发布，敬请理解

1 数据的表示

1.1 进制转换

1、任意进制转十进制

二进制转十进制

八进制转十进制

十六进制转十进制

方法：按权展开

2、十进制转任意进制

十进制转二进制

十进制转八进制

十进制转十六进制

方法;除模取余，倒序排列

3、二进制转换为其他进制

二进制转八进制

二进制转十六进制

方法：位数对应，直接转换

1.2 机器编码方式

二进制表示是计算机实现成本最低的方式，通过电平的高低、闭合等方式即可判别和存储

计算机只能看到二进制，其余进制都是给人看的，方便人的操作与记录

（1）为了区分正数、负数，提出符号位，形成了原码的概念

原码：将数转换为二进制位，然后正数的最高位添0，负数的最高位添1，最高位表示符号

（2）为了将减法变为加法，减少运算器内部的逻辑单元，出现了反码的概念

反码：正数的反码和原码相同，负数的反码，符号位不变，其余位取反

（3）为了解决0存在+0和-0两种不同的表示方法的问题，出现了补码的概念

补码：正数的补码和反码相同，负数的补码等于反码加1

（4）任何一个二进制数都可以转换成N=S×2^P的形式，P作为指数，又被称为阶码

阶码：阶码固定的数称为定点数，阶码可以改变的数称为浮点数

（5）为了解决浮点数表示法中阶码无限小时的溢出问题，出现了移码的概念

移码：移码又叫增码或偏置码，其符号位用“1”表示正数，用“0”表示负数，数值部分与补码相同

1.3 浮点数的表示

浮点数采用科学计数法公式，如下：

$N=M*{R}^{e}$

式中，N为浮点数，M为尾数，R为基数，e为指数

浮点数的计算：对阶 -> 尾数计算 -> 结果格式化

结果格式化：浮点数的保证整数部分为1位且不能为0，例如 $1.19 \times {10}^{3}$

2 计算机结构

计算机：主机 + 外设

主机：CPU + 存储器

外设：输入设备 + 输出设备

CPU：运算器 + 控制器

存储器：内存（主存储器）+ 外存

运算器：算数逻辑单元ALU、累加寄存器AC、数据缓冲寄存器DR、状态条件寄存器PSW

控制器：程序计数器PC、指令寄存器IR、指令译码器、时序部件

CPU架构分为两种经典结构：

（1）冯.诺依曼结构（普林斯顿结构）：取指令、取数据共享同一条总线，不能同时进行

（2）哈佛结构：取指令、取数据有各自独立的总线，两者可以同时进行

后来出现了改进的哈佛结构，即结合了冯.诺依曼结构和哈佛结构两者的优点

3 Flynn分类法

Flynn分类：一种计算机体系结构分类方法

（1）单指令流单数据流SISD

（2）单指令流多数据流SIMD

（3）多指令流单数据流MISD

（4）多指令流多数据流MIMD

4 CISC与RISC

指令系统类型：

（1）CISC（Complex Instruction Set Computer）：复杂指令集计算机

（2）RISC（Reduced Instruction Set Computer）：精简指令集计算机

5 流水线技术

5.1 流水线的概念

流水线：程序在执行多条指令重叠进行操作的一种准并行处理实现技术

一般将一条操作分为：取指 -> 分析 -> 执行

流水线操作即：

取指令1完毕后马上取值下一条指令2

取指令2的同时，分析指令1，分析完毕马上分析下一条指令2

分析指令2的同时，执行指令1，执行完毕马上执行下一条指令2

看起来取指、分析、执行三个步骤在同时进行，就像流水一样不间断

5.2 流水线的时间计算

指令周期：流水线指令周期为一条指令中执行时间最长的一段步骤的时间

1条指令执行时间 + (指令条数-1) * 流水线周期

（1）理论公式： ${t}_{1}+{t}_{2}+{t}_{3}+......+{t}_{k}+(n-1)*\Delta t$

（2）实践公式： $(k+n-1)*\Delta t$

式中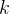，为一条指令的步骤数，为指令总数， $\Delta t$ 为指令周期

【例题1】

一条指令分为取值、分析、执行三个部分，每部分执行时间分别为2ns、1ns、1ns，问流水线周期是多少？100条指令全部执行完毕需要多少时间？

解答：

流水线周期 $\Delta t=max(2, 2, 1)ns=2ns$

100条指令执行时间 $T=2+2+1+(100-1) \times 2=203ns$

若有理论公式计算的答案，则优先选择该答案，否则选择实践公式计算的答案

5.3 流水线的吞吐率计算

1、流水线的吞吐率（Though Put rate，TP）：在单位时间内流水线所完成的任务数量或输出的结果数量。计算公式如下：

$TP=\frac{n}{T}$

式中，为指令条数，为流水线执行时间

以5.2中的例题1为例， $T P = \frac{100}{203} \approx 49.26$

2、流水线的最大吞吐率计算公式为：

${TP}_{max}=\lim_{n \to \infty}\frac{n}{(k+n-1)*\Delta t}=\frac{1}{\Delta t}$

以5.2中的例题1为例， ${T P}_{m a x} = \frac{1}{2} = 50$

5.4 流水线的加速比计算

流水线加速比：完成同样一项任务，不使用流水线与使用流水线所用的时间比值称为流水线加速比。计算公式为：

$S=\frac{{T}_{1}}{{T}_{2}}$

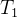式中， ${T}_{1}$ 为不使用流水线完成一项任务的时间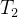， ${T}_{2}$ 为使用流水线完成一项任务的时间

以5.2中的例题1为例， $S=\frac{(2+2+1)\times 100}{203}=\frac{500}{203}\approx 2.46$

5.5 流水线的效率计算

流水线的效率：流水线的设备利用率，在时空图图上，流水线的效率定义为n个任务占用的时空区与k个流水段总的时空区之比。计算公式为：

$E=\frac{{T}_{0}}{k{T}_{k}}$

式中， ${T}_{0}$ 为n个任务占用的时空区，k为流水段个数， ${T}_{k}$ 为1个流水段占用的时空区

【例题2】

一条指令分为S1、S2、S3、S4一共四个部分，每部分执行时间分别为Δt、Δt、Δt、3Δt，求使用流水线方式连续处理4条该指令的效率

解答：

$E = \frac{(Δ t + Δ t + Δ t + 3 Δ t) \times 4}{(Δ t + Δ t + Δ t + 3 Δ \times 4) \times 4} = \frac{6}{15} = 40$

上述计算式中的4均表示4条指令

6 存储系统

6.1 层次化存储结构

速度	存储器类型	说明	容量
快	CPU	寄存器	以Bytes为单位
较快	Cache（高速缓存）	按内容存取	以KB、MB为单位
较慢	内存（主存）	CPU可以直接操作内存	以MB（很少）、GB为单位
慢	外存（辅存）	硬盘、光盘、U盘等	以MB（基本淘汰）、GB、TB为单位

6.2 Cache概念

Cache功能：提高CPU数据输入输出的速率，即突破CPU与存储系统间数据传送带宽的限制

使用 “Cache+主存储器” 的系统进行读操作的平均周期为：

${t}_{3}=h*{t}_{1}+(1-h)*{t}_{2}$

上式中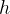，代表对Cache的访问命中率， (1-h) 称为失效率（未命中率）， ${t}_{1}$ 表示Cache的周期时间， ${t}_{2}$ 表示主存储器周期时间

【例题3】

使用 “Cache+主存储器” 的系统进行读操作，读取Cache的周期时间为1ns，读取主存储器的周期时间为1ms，对Cache的访问命中率为95%，求该系统读操作的平均周期时间

解答：

$t=0.95 \times 1 + (1-0.95) \times 1000=50.95 ns$

引入Cache后，读取操作效率提高了近20倍

6.3 局部性原理

（1）时间局部性：计算机在某时段集中访问某一指令。比如频繁的给某一个变量执行+1操作

（2）空间局部性：计算机在某时段集中访问某一空间的数据。比如给一段连续的地址空间赋初值

工作集理论：工作集是进程运行时频繁访问的页面集合

6.4 主存储器

1、主存分类

（1）随机存取存储器（RAM）：掉电丢失数据

DRAM（Dynamic RAM）、SDRAM

SRAM（Stattic RAM）

（2）只读存ROM）：掉电之后不丢失数据

MROM（Mask ROM）

PROM（Programmable ROM）

EPROM（Erasable PROM）

闪存（Flash Memory）

2、主存编址

8*4位的存储器：地址空间位8个单元，每个地址按4bit编址

8*8位的存储器：地址空间位8个单元，每个地址按8bit编址

16*4位的存储器：地址空间位16个单元，每个地址按4bit编址

例题：

内存地址从AC000H到C7FFFH，共有____K个地址单元，如果该内存地址按字（16bit）编址，由285片存储器芯片构成。已知构成此内存的芯片每片有16K个存储单元，则该芯片每个存储单元存储____位

解答：

地址空间单位：C7FFF+1-AC000=C8000-AC000=1C000H

用二进制表示为：0001 1100 0000 0000 0000

转换为K为单位，即除以 $2^{10}$ ，右移10个0，即为：

0001 1100 00 K= 0111 0000 K = (64+32+16)K = 112K

由存储器空间等价，可得： $112K \times 16=28 \times 16K \times ?$

解得该芯片每个存储单元存储： $\frac{112K \times 16}{28 \times 16K}=4bit$

答案为：112，4

6.5 磁盘结构与参数

磁盘：磁道+扇区

存取时间 = 寻道时间+等待时间（平均定位时间+转动延迟）

寻道时间：磁头移动到磁道所需要的时间

等待时间：等待读写的扇区转到磁头下方所用的时间

【例题4】

假设某磁盘的每个磁道划分成11个物理块，每块存放1个逻辑记录，逻辑记录R0~R10存放在同一磁道上，记录的存放顺序如下表所示：

物理块	1	2	3	4	5	6	7	8	9	10	11
逻辑记录	R0	R1	R2	R3	R4	R5	R6	R7	R8	R9	R10

如果磁盘的旋转周期为33ms，磁头当前处在的开始处。若系统使用单缓冲区顺序处理这些记录，每个记录处理时间为3ms，则处理这11个记录的最长时间为___，若对信息进行优化分布后，处理11个记录的最少时间为___

解答：

由题，磁盘的旋转周期为33ms，一共11个逻辑记录，因此读取每个逻辑记录需要3ms，每个记录的处理时间为3ms，因为是单缓冲区顺序处理，所以当处理完逻辑记录R0时，磁头已经在R2开始处，要想处理R1，需要磁盘再转一整圈

转到R0开始：0 ms（磁头当前处在的开始处）

转到R1开始：33+3 ms

......

转到R10开始：(33+3) x 10 = 360 ms

读取R10开始：360 + 3 = 363 ms

处理R10结束：363 + 3 = 366 ms

若进行信息的优化分布，则磁盘无需再转一整圈，共计耗费时间为：(3+3)x11=66 ms

最终答案为：366 ms，66 ms

7 总线系统

（1）内部总线

（2）系统总线

数据总线、地址总线、控制总线

（3）外部总线

8 系统可靠性

8.1 串联系统

串系统如下图所示

若每一个子系统的可靠度分别为： ${R}_{1}$ ， ${R}_{2}$ ，...， ${R}_{n}$

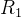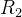可靠性计算公式如下：

$R={R}_{1} \times {R}_{2} \times ... \times {R}_{n}$

若每一个子系统的失效率分别为： ${\lambda }_{1}$ ， ${\lambda }_{2}$ ，...， ${\lambda }_{n}$

失效率近似计算公式如下：

$\lambda = {\lambda }_{1}+{\lambda }_{2}+...+{\lambda }_{n}$

8.2 并联系统

并联系统如下图所示

若每一个子系统的可靠度分别为： ${R}_{1}$ ， ${R}_{2}$ ，...， ${R}_{n}$

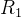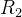可靠性计算公式如下：

$R=1-(1-{R}_{1}) \times (1-{R}_{2}) \times ... \times (1-{R}_{n})$

若所有子系统的失效率均为 $\lambda$

失效率计算公式如下：

$\mu = \frac{1}{\frac{1}{\lambda} \sum_{j=1}^{n}\frac{1}{j}}$

8.3 模冗余系统

模冗余系统如下图所示

模冗余系统由N个相同的子系统和一个表决器组成，若每个子系统的可靠性为 ${R}_{0}$

可靠性计算公式为：

$R=\sum_{i=n+1}^{N}C_{N}^{j}\times R_{0}^{i}(1-{R}_{0})^{N-i}$

8.4 混合系统

混合系统如下图所示

混合系统中既有串联系统部分，也有并联系统部分，其可靠性计算需要使用整体替换法，即求出某部分的可靠性，再再此部分用一个系统代替

例如上图可靠性计算为： $R \times (1-(1-R)^{3}) \times (1-(1-R)^{2})$

9 校验码

9.1 校验码概念

检错：检查传输是否发生错误

纠错：检查错误后纠正错误

码距：一个编码系统的码距是整个编码系统中任意两个码字的最小距离

在一个码组内为了检测e个误码，要求最小码距d应该满足：d >= e+1
在一个码组内为了纠正t个误码，要求最小码距d应该满足：d >= 2t+1

9.2 循环校验码

循环校验码（CRC，Cyclic Redundancy Check）

利用生成多项式为k个数据位产生r个校验码来进行编码，其编码长度为k+r，其格式为：

若数据码占k位，则校验码占n-k位，n为CRC码的字长，校验码位数越多，校验能力就越强

在求CRC编码时，采用模2除法

模2除法是指在做除法运算的过程中不计其进位的除法

【例题5】

原始报文为：11001010101，生成的多项式为 ${x}^{4}+{x}^{3}+x+1$ ，求对其进行CRC编码？

解答：

多项式编码为：11011，长度为5位，因此余数为4位，所以在原始报文后补4个0

然后，计算110010101010000 模2除 11011的余数，为0011

CRC编码为：110010101010011

该编码的数据码占11位，校验码占4位，共15位

9.3 海明校验码

考察重点

海明码（Hamming Code）

设海明码的数据位为n位，校验位为k位，则

${2}^{k}>=n+k+1$

【例题6】

求信息1011的海明码

解答：

（1）由题意，n=4，因 ${2}^{3}>=4+3+1$ ，得出k=3，校验码放在第1、2、4位，一共7位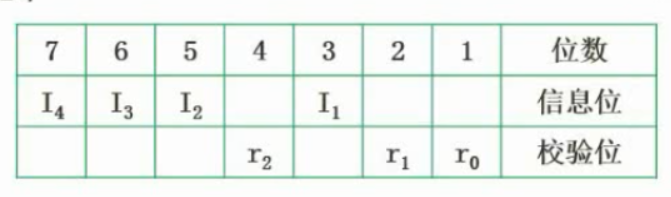

（2）I4=1，I3=0，I2=1，I1=1

将编码位数拆分成2的阶乘的组合，如下

编码位	海明码下标	校验组合	海明码
H1（r0）	1	-	I4 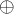$\oplus$ I2 $\oplus$ I1 = 1
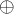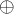H2（r1）	2	-	I4 $\oplus$ I3 $\oplus$ I1 = 0
H3（I1）	3=1+2	r0、r1	1
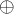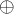H4（r2）	4	-	I4 $\oplus$ I3 $\oplus$ I2 = 0
H5（I2）	5=1+4	r0、r2	1
H6（I3）	6=2+4	r1、r2	0
H7（I4）	7=1+2+4	r0、r1、r2	1

（3）求得 r2=0，r1=0，r0=1

（4）因此海明码为 1010101

海明码还有纠错能力

在例题6中，若收到信息为1011101，再次计算：

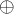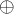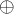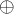r2 $\oplus$ I4 $\oplus$ I3 $\oplus$ I2 = 1，

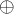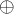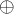r1 $\oplus$ I4 $\oplus$ I3 $\oplus$ I1 = 0，

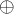r0 $\oplus$ I4 $\oplus$ I2 $\oplus$ I1 = 0，

计算结果100的十进制为4，说明第4位出现错误，即校验位r2出现错误，将其取反即可纠正

纠正后的海明码为 1010101

相关阅读:
[Qt网络编程]之UDP通讯的简单编程实现
 Vue Router的使用
 在子页面（弹窗）的表单中填写完信息点击提交按钮后，如何将表单中的内容传递给父页面中的table
多线程与高并发（三）—— 源码解析 AQS 原理
 java源码系列：HashMap底层存储原理详解——7、演示1.7底层实现原理验证-如何使用链表存储
 Xline 源码解读（四）—— CURP 状态机引擎
 树莓派登录后运行PYTHON
Java 异步编程 (5 种异步实现方式详解)
（附源码）springboot企业合同管理系统毕业设计 161456
[Power BI] 认识Power Query和M语言
原文地址：https://blog.csdn.net/lishan132/article/details/126907718

软考中级-软件设计师-第2章 计算机组成与体系结构

1 数据的表示

1.1 进制转换

1.2 机器编码方式

1.3 浮点数的表示

2 计算机结构

3 Flynn分类法

4 CISC与RISC

5 流水线技术

5.1 流水线的概念

5.2 流水线的时间计算

5.3 流水线的吞吐率计算

5.4 流水线的加速比计算

5.5 流水线的效率计算

6 存储系统

6.1 层次化存储结构

6.2 Cache概念

6.3 局部性原理

6.4 主存储器

6.5 磁盘结构与参数

7 总线系统

8 系统可靠性

8.1 串联系统

8.2 并联系统

8.3 模冗余系统

8.4 混合系统

9 校验码

9.1 校验码概念

9.2 循环校验码

9.3 海明校验码

软考中级-软件设计师-第2章计算机组成与体系结构