简单函数模拟优化器

简单函数模拟优化器

优化器是引导神经网络更新参数的工具，深度学习在计算出损失函数之后，需要利用优化器来进行反向传播，完成网络参数的更新。在这个过程中，便会使用到优化器，优化器可以利用计算机数值计算的方法来获取损失函数最小的网络参数。
接下来，我们利用简单的数学模型构建一个模拟的优化器。

首先，构建相关函数

import numpy as np
import matplotlib.pyplot as plt

#打印结果
def print_info( k, x_0, y_0, f2):
    print('迭代次数：{}'.format(k))
    print('极值点：【x_0】：{} 【y_0】：{}'.format(x_0, y_0))
    print('函数的极值：{}'.format(f2))

#绘制效果图
def draw_process(w):
    X = np.arange(0, 1.5, 0.01)  # 起始、终止、步长
    Y = np.arange(-1, 1, 0.01)
    [x, y] = np.meshgrid(X, Y)  # 将x中每一个数据和y中每一个数据组合生成很多点,然后将这些点的x坐标放入到X中,y坐标放入Y中,并且相应位置是对应的
    f = x ** 3 - y ** 3 + 3 * x ** 2 + 3 * y ** 2 - 9 * x
    plt.contour(x, y, f, 20)
    plt.plot(w[:, 0], w[:, 1], 'g*', w[:, 0], w[:, 1])
    plt.show()

#生成函数
def fn(x, y):
    return x ** 3 - y ** 3 + 3 * x ** 2 + 3 * y ** 2 - 9 * x

#对x求偏导
def dx(x):
    return 3 * x ** 2 + 6 * x - 9

#对y求偏导
def dy(y):
    return - 3 * y ** 2 + 6 * y

"""
    函数: f(x) = x**3 - y**3 + 3 * x**2 + 3 * y**2 - 9 * x
    最优解: x = 1, y = 0
    极小值: f(x,y) = -5
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

其次，构建各种优化器函数：

1、Momentum（使用动量的随机梯度下降)

SGD每次都会在当前位置沿梯度负方向更新，不会考虑先前的梯度方向及大小；Momentum则是通过引入一个新的变量v去积累之前的梯度，从来可以加速网络的学习过程，也就是说如果当前时刻的梯度方向与之前时刻累计的梯度方向一致，那么梯度会加强，梯度下降的幅度更大，反之，梯度下降的幅度会降低。

Monmentum涉及到的函数与参数：

生成函数：z = f(x,y)
损失函数：Loss()
初始参数：weight
初始速度：v
学习率：lr
动量参数：alpha
误差阈值：epsilon

大致流程：

(1)从训练集中采集把后含m个样本{x1,······,xm}的小批量，对应目标yi。
(2)计算梯度估计：

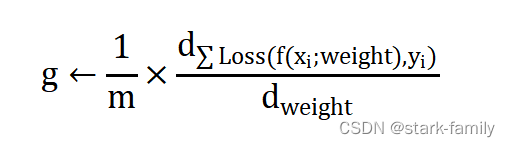
(3)计算速度更新：

(4)应用更新：

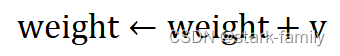
(5)重复执行（1）到（4），直到达到终止条件为止，终止条件一般是迭代次数达到iters或者预测值与真实值之间的误差小于误差阈值epsilon。

模拟优化器的具体代码：

#使用动量的随机梯度下降
def momentum(x_0,y_0):
    f1, f2 = fn(x_0, y_0), 0 # f1为预测值，f2为真实值（目标值）
    w = np.array([x_0, y_0])  # 每次迭代后的函数值，用于绘制梯度曲线
    k = 0  # 当前迭代次数

    lr = 0.01 #学习率
    alpha = 0.9 #动量参数
    iters = 100000 #迭代次数上限
    epsilon = 1e-10 #误差阈值
    v = 0.0 #速度

    while True:
        if abs(f1 - f2) <= epsilon or k > iters:
            break

        f1 = fn(x_0, y_0)
        g = np.array([dx(x_0), dy(y_0)])
        v = alpha * v - lr * g  # 速度更新
        x_0, y_0 = np.array([x_0, y_0]) + v  # 应用更新

        f2 = fn(x_0, y_0)

        w = np.vstack((w, (x_0, y_0)))
        k += 1
    print_info(k, x_0, y_0, f2)
    draw_process(w)

momentum(x_0=0.5,y_0=0.5)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

迭代次数：195
极值点：【x_0】：0.9999837364060098 【y_0】：-1.2415641058597648e-05
函数的极值：-4.999999997950532
1
2
3

效果图

2、AdaGrad（自适应梯度下降）

针对SGD与Momentum存在的问题，AdaGrad（Adaptive Gradient）是在SGD基础上引入二阶动量，能够对不同的参数使用不同的学习率进行更新，对于梯度较大的参数，那么学习率就会变得较小；而对于梯度较小的参数，那么学习率就会变得较大，这样就会使在陡峭的区域下降速度快，平缓的区域下降速度慢。

AdaGrad涉及到的函数与参数：

生成函数：z = f(x,y)
损失函数：Loss()
初始参数：weight
梯度累计变量：r (伽马）
学习率：lr
小常数：delta，（为了数值稳定，一般设置为10^-7）
误差阈值：epsilon

大致流程：

初始化累计变量 r = 0
(1)从训练集中采集把后含m个样本{x1,······,xm}的小批量，对应目标yi。
(2)计算梯度估计：

(3)累计平方梯度：

(4)计算参数更新：

(5)应用更新：

(5)重复执行（1）到（4），直到达到终止条件为止，终止条件一般是迭代次数达到iters或者预测值与真实值之间的误差小于误差阈值epsilon。

模拟优化器的具体代码：

##使用学习率自适应的随机梯度下降
def AdaGrad(x_0,y_0):
    f1, f2 = fn(x_0, y_0), 0 # f1为预测值，f2为真实值（目标值）
    w = np.array([x_0, y_0])  # 每次迭代后的函数值，用于绘制梯度曲线
    k = 0  # 当前迭代次数

    lr = 0.01 #学习率
    delta = 1e-7 #小常数
    iters = 100000 #迭代次数上限
    epsilon = 1e-10 #误差阈值
    r = 0.0 #梯度累计变量

    while True:
        if abs(f1 - f2) <= epsilon or k > iters:
            break

        f1 = fn(x_0, y_0)
        g = np.array([dx(x_0), dy(y_0)])
        r = r + np.dot(g,g)
        #np.dot(a, b), 其中a为一维的向量，b为一维的向量，这里a和b都是np.ndarray类型的（一维的所以是向量叉乘）
        #两个不共线的向量叉乘的结果是与这两个向量所在平面垂直的一个向量（外积），两个向量点积的结果是一个数值（内积）。

        delta_weight = np.dot(-lr / (delta + pow(r, 1 / 2)), g) #参数更新
        x_0, y_0 = np.array([x_0, y_0]) + delta_weight #应用更新

        f2 = fn(x_0, y_0)

        w = np.vstack((w, (x_0, y_0)))
        k += 1
    print_info(k, x_0, y_0, f2)
    draw_process(w)

AdaGrad(x_0=0.5,y_0=0.5)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

迭代次数：13691
极值点：【x_0】：0.999999963104632 【y_0】：0.00016986797379206335
函数的极值：-4.999999913439508
1
2
3

效果图

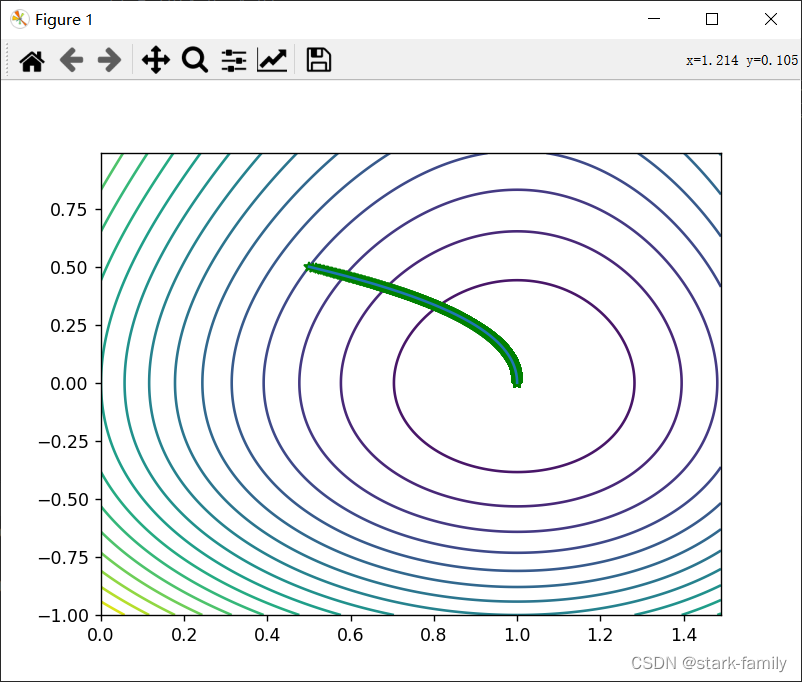
3、RMSProp

RMSProp算法修改AdaGrad以在非凸设定下效果更好，改变梯度积累为指数加权的移动平均。Adagrad旨在应用于图问题是快速收敛。当应用于非凸函数训练神经网络时，学习轨迹可能穿过了很多不同的结构，最后到达一个局部是非碗区域。AdaGrad根据平方梯度的整个历史收缩学习率，可能使得学习率在达到这样的凸结构前就变得太小了。
RMSProp使用指数衰减平均一丢弃遥远过去的历史，使其能够在找到凸碗结构后快速收敛，它就像一个初始化与该碗状结构的AdaGrad算法实例。

RMSProp涉及到的函数与参数：

生成函数：z = f(x,y)
损失函数：Loss()
初始参数：weight
梯度累计变量：r (伽马）
学习率：lr
衰减速率：ρ （代码里我们那就用p表示）
小常数：delta，（δ，为了数值稳定，建议默认为为10^-6）
误差阈值：epsilon （ε）

大致流程：

初始化累计变量 r = 0
(1)从训练集中采集把后含m个样本{x1,······,xm}的小批量，对应目标yi。
(2)计算梯度估计：

(3)累计平方梯度：

(4)计算参数更新：

(5)应用更新：

(5)重复执行（1）到（4），直到达到终止条件为止，终止条件一般是迭代次数达到iters或者预测值与真实值之间的误差小于误差阈值epsilon。

模拟优化器的具体代码：

#使用RMSProp的随机梯度下降
def RMSProp(x_0,y_0):
    f1, f2 = fn(x_0, y_0), 0 # f1为预测值，f2为真实值（目标值）
    w = np.array([x_0, y_0])  # 每次迭代后的函数值，用于绘制梯度曲线
    k = 0  # 当前迭代次数

    lr = 0.01 #学习率
    delta = 1e-6 #小常数
    p = 0.5  # 衰减速率
    iters = 100000 #迭代次数上限
    epsilon = 1e-10 #误差阈值
    r = 0.0 #梯度累计变量

    while True:
        if abs(f1 - f2) <= epsilon or k > iters:
            break

        f1 = fn(x_0, y_0)
        g = np.array([dx(x_0), dy(y_0)])
        r = p * r + (1 - p) * np.dot(g,g)
        #np.dot(a, b), 其中a为一维的向量，b为一维的向量，这里a和b都是np.ndarray类型的（一维的所以是向量叉乘）
        #两个不共线的向量叉乘的结果是与这两个向量所在平面垂直的一个向量（外积），两个向量点积的结果是一个数值（内积）。

        delta_weight = np.dot(-lr / pow(delta + r, 1 / 2), g) # 参数更新
        x_0, y_0 = np.array([x_0, y_0]) + delta_weight #应用更新

        f2 = fn(x_0, y_0)

        w = np.vstack((w, (x_0, y_0)))
        k += 1
    print_info(k, x_0, y_0, f2)
    draw_process(w)

RMSProp(x_0=0.5,y_0=0.5)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

迭代次数：100001
极值点：【x_0】：1.0049930572293455 【y_0】：0.0
函数的极值：-4.999850291797012
1
2
3

效果图

很明显，RMSProp迭代的时间更久了。

4、Adam (Adaptive moments）

Adam是另一种学习率自适应的优化算法。

Adam是将Momentum与RMSProp结合起来的一种算法，引入了Momentum的一阶动量来累计梯度与RMSProp的二阶动量可以使得收敛速度快的同时使得波动幅度小，然后在此基础上增加了两个修正项，能够实现参数自新。

Adam优化器具有以下优点：

1. 实现简单，计算高效，对内存需求少
2. 参数的更新不受梯度的伸缩变换影响
3. 超参数具有很好的解释性，且通常无需调整或仅需很少的微调
4. 更新的步长能够被限制在大致的范围内（初始学习率）
5. 能自然地实现步长退火过程（自动调整学习率）
6. 很适合应用于大规模的数据及参数的场景
7. 适用于不稳定目标函数
8. 适用于梯度稀疏或梯度存在很大噪声的问题

Adam涉及到的函数与参数：

生成函数：z = f(x,y)
损失函数：Loss()
初始参数：weight
梯度累计变量：s，r (伽马）
学习率：lr （步长，建议默认为0.001）
矩估计衰减速率：ρ1和ρ2在区间[0,1)内。（建议默认为：分别为0.9和0.999） （代码里我们暂用p1与p2表示）
小常数：delta，（δ，为了数值稳定，建议默认为为10^-8）
误差阈值：epsilon （ε）

大致流程：

初始化一阶和二阶矩变量 s = 0，r = 0
初始化时间步 t = 0
(1)从训练集中采集把后含m个样本{x1,······,xm}的小批量，对应目标yi。
(2)计算梯度估计：

(3)更新有偏一阶矩估计：

(4)更新有偏二阶矩估计：

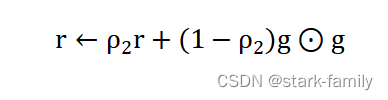
(5)修正一阶矩的偏差：

(6)修正一阶矩的偏差：

(7)计算参数更新：

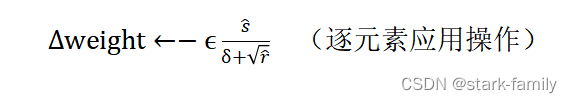
(8)应用更新：

(5)重复执行（1）到（4），直到达到终止条件为止，终止条件一般是迭代次数达到iters或者预测值与真实值之间的误差小于误差阈值epsilon。

模拟优化器的具体代码：

#使用动量的随机梯度下降
def Adam(x_0,y_0):
    f1, f2 = fn(x_0, y_0), 0 # f1为预测值，f2为真实值（目标值）
    w = np.array([x_0, y_0])  # 每次迭代后的函数值，用于绘制梯度曲线
    k = 0  # 当前迭代次数

    lr = 0.001 # 学习率
    delta = 1e-8 # 小常数
    iters = 100000 # 迭代次数上限
    epsilon = 1e-10 # 误差阈值

    p1 = 0.9  # 一阶矩估计指数衰减速率
    p2 = 0.999  # 二阶矩估计指数衰减速率
    s = 0  # 一阶矩估计累计平方梯度（一阶矩变量）
    r = 0  # 二阶矩估计累计平方梯度（二阶矩变量）
    t = 0  # 初始化时间步

    while True:
        if abs(f1 - f2) <= epsilon or k > iters:
            break

        f1 = fn(x_0, y_0)
        g = np.array([dx(x_0), dy(y_0)])

        t = t + 1
        s = p1 * s + (1 - p1) * g
        r = p2 * r + np.dot((1 - p2) * g, g)
        # np.dot(a, b), 其中a为一维的向量，b为一维的向量，这里a和b都是np.ndarray类型的（一维的所以是向量叉乘）
        # 两个不共线的向量叉乘的结果是与这两个向量所在平面垂直的一个向量（外积），两个向量点积的结果是一个数值（内积）。

        s1 = s / (1 - pow(p1, t))  # s1为修正后的一阶矩偏差
        r1 = r / (1 - pow(p2, t))  # r1为修正后的二阶矩偏差

        delta_weight = (-lr * s1) / (pow(r1, 1 / 2) + delta)  # 参数更新
        x_0, y_0 = np.array([x_0, y_0]) + delta_weight  # 应用更新

        f2 = fn(x_0, y_0)

        w = np.vstack((w, (x_0, y_0)))
        k += 1
    print_info(k, x_0, y_0, f2)
    draw_process(w)

Adam(x_0=0.5,y_0=0.5)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

迭代次数：2784
极值点：【x_0】：0.9999999989212892 【y_0】：4.760876046908952e-05
函数的极值：-4.9999999932003245
1
2
3

效果图

很明显，Adam迭代得更快了。