数据结构——树

---

前言

本文介绍了树的相关概念及二叉树：

---

一、树的定义

1.1 什么是树？

树是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就
是说它是根朝上，而叶朝下的。

1.1.1树的特点

树具有以下特点：

1. 每个结点有零个或多个子结点；
2. 没有父结点的结点为根结点；
3. 每一个非根结点只有一个父结点；
4. 每个结点及其后代结点整体上可以看做是一棵树，称为当前结点的父结点的一个子树；

1.2 树的相关术语

1.2.1 结点的度：

一个结点含有的子树的个数称为该结点的度；
例如：A节点含有6个子树（B , C,D,E,F,G）

1.2.2 叶结点：

度为0的结点称为叶结点，也可以叫做终端结点
例如：B,C,H,I,P,Q,K,L,M,N

1.2.3分支结点：

度不为0的结点称为分支结点，也可以叫做非终端结点
除了叶节点都是。

1.2.4结点的层次：

从根结点开始，根结点的层次为1，根的直接后继层次为2，以此类推

1.2.5结点的层序编号：

将树中的结点，按照从上层到下层，同层从左到右的次序排成一个线性序列，把他们编成连续的自然数。

1.2.6树的度：

树中所有结点的度的最大值
该树的最大值为6。

1.2.7树的高度(深度)：

树中结点的最大层次，该树为4

1.2.8森林：

m（m>=0）个互不相交的树的集合，将一颗非空树的根结点删去，树就变成一个森林；给森林增加一个统一的根结点，森林就变成一棵树

1.2.9孩子结点：

一个结点的直接后继结点称为该结点的孩子结点

1.2.10双亲结点(父结点)：

一个结点的直接前驱称为该结点的双亲结点

1.2.11兄弟结点：

同一双亲结点的孩子结点间互称兄弟结点

二、二叉树

2.1 二叉树的基本定义

二叉树就是度不超过2的树(每个结点最多有两个子结点)

2.1.1 满二叉树

一个二叉树，如果每一个层的结点树都达到最大值，则这个二叉树就是满二叉树。

2.1.2 完全二叉树

叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树

2.2 二叉树的遍历

2.2.1 前序遍历

先访问根结点，然后再访问左子树，最后访问右子树

2.2.2 中序遍历

先访问左子树，中间访问根节点，最后访问右子树

2.2.3 后序遍历

先访问左子树，再访问右子树，最后访问根节点

2.2.4 层序遍历

所谓的层序遍历，就是从根节点（第一层）开始，依次向下，获取每一层所有结点的值
那么层序遍历的结果是：EBGADFHC

三、平衡树

学前回顾：
之前我们学习过二叉查找树，发现它的查询效率比单纯的链表和数组的查询效率要高很多，大部分情况下，确实是
这样的，但不幸的是，在最坏情况下，二叉查找树的性能还是很糟糕。
例如我们依次往二叉查找树中插入9,8,7,6,5这9个数据，那么最终构造出来的树是长得下面这个样子：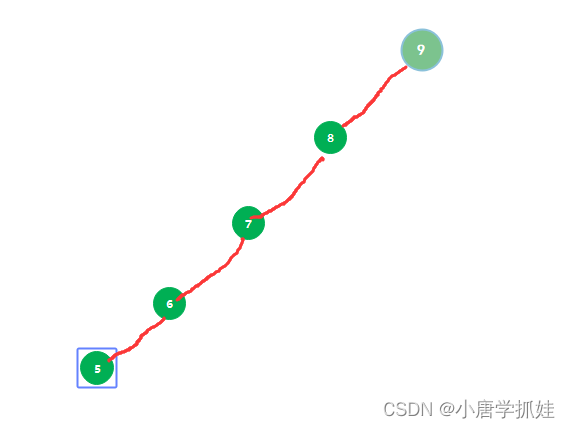

我们会发现，如果我们要查找5这个元素，查找的效率依旧会很低。效率低的原因在于这个树并不平衡，全部是向
左边分支，如果我们有一种方法，能够不受插入数据的影响，让生成的树都像完全二叉树那样，那么即使在最坏情
况下，查找的效率依旧会很好。

3.1 查找树

3.1.1 查找树的定义

为了保证查找树的平衡性，我们需要一些灵活性，因此在这里我们允许树中的一个结点保存多个键。确切的说，我
们将一棵标准的二叉查找树中的结点称为2-结点(含有一个键和两条链)，而现在我们引入3-结点，它含有两个键和
三条链。2-结点和3-结点中的每条链都对应着其中保存的键所分割产生的一个区间。

3.2 红黑树

---

总结