`算法知识` 模意义下的乘法逆元

In computer science, the analysis of algorithms is the process of finding the computational complexity of algorithms—the amount of time, storage, or other resources needed to execute them. Usually, this involves determining a function that relates the size of an algorithm’s input to the number of steps it takes (its time complexity) or the number of storage locations it uses (its space complexity). An algorithm is said to be efficient when this function’s values are small, or grow slowly compared to a growth in the size of the input. Different inputs of the same size may cause the algorithm to have different behavior, so best, worst and average case descriptions might all be of practical interest. When not otherwise specified, the function describing the performance of an algorithm is usually an upper bound, determined from the worst case inputs to the algorithm.

The term “analysis of algorithms” was coined by Donald Knuth.[1] Algorithm analysis is an important part of a broader computational complexity theory, which provides theoretical estimates for the resources needed by any algorithm which solves a given computational problem. These estimates provide an insight into reasonable directions of search for efficient algorithms.

In theoretical analysis of algorithms it is common to estimate their complexity in the asymptotic sense, i.e., to estimate the complexity function for arbitrarily large input. Big O notation, Big-omega notation and Big-theta notation are used to this end. For instance, binary search is said to run in a number of steps proportional to the logarithm of the size n of the sorted list being searched, or in O(log n), colloquially “in logarithmic time”. Usually asymptotic estimates are used because different implementations of the same algorithm may differ in efficiency. However the efficiencies of any two “reasonable” implementations of a given algorithm are related by a constant multiplicative factor called a hidden constant.

Exact (not asymptotic) measures of efficiency can sometimes be computed but they usually require certain assumptions concerning the particular implementation of the algorithm, called model of computation. A model of computation may be defined in terms of an abstract computer, e.g. Turing machine, and/or by postulating that certain operations are executed in unit time. For example, if the sorted list to which we apply binary search has n elements, and we can guarantee that each lookup of an element in the list can be done in unit time, then at most log2(n) + 1 time units are needed to return an answer.

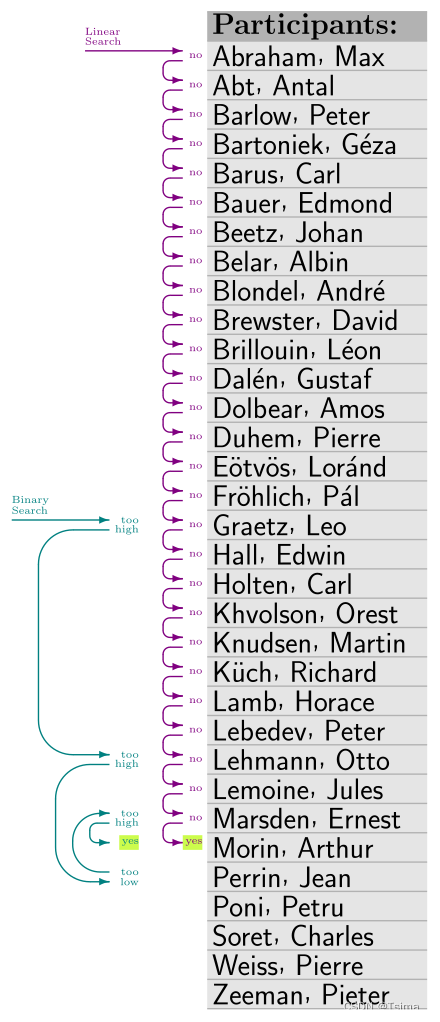
For looking up a given entry in a given ordered list, both the binary and the linear search algorithm (which ignores ordering) can be used. The analysis of the former and the latter algorithm shows that it takes at most log2 n and n check steps, respectively, for a list of size n. In the depicted example list of size 33, searching for “Morin, Arthur” takes 5 and 28 steps with binary (shown in cyan) and linear (magenta) search, respectively.

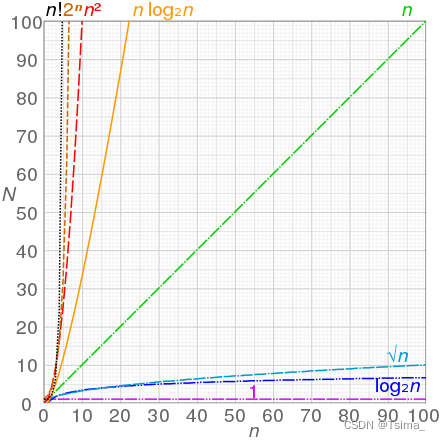
Graphs of functions commonly used in the analysis of algorithms, showing the number of operations N versus input size n for each function