Numpy+PyTorch基础《python深度学习----基于pytorch》

第1章 Numpy基础

Numpy封装了一个新的数据类型ndarray(N-dimensional Array), 它是一个多维数组对象

1.1.1 从已有的数据中创建数组

1. 将列表转换为ndarray:

import numpy as np 
lst1 = [3.14, 1, 3]
nd1 = np.array(lst1)
1
2
3

2. 嵌套列表可以转换为多维ndarray(列表换成元组也同样适用)

1.1.2利用random模块生成数组

随机数种子seed只有一次有效，在下一次调用产生随机数函数前没有设置seed，则还是产生随机数。

1.1.3 创建特定形状的多维数组

np.ones_like 函数：返回一个用1填充的跟输入 形状和类型 一致的数组

1.1.4 利用arange, linspace函数生成数组

arange([start,] stop[,step, ], dtype=None)
np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

1.3 Numpy的算数运算

1.3.1 对应元素相乘

A*B， 即 np.multiply(A, B) 矩阵A和B的对应元素相乘
Numpy数组不仅可以和数组进行对应元素相乘，还可以和单一数值（即标量）进行运算。运算时，Numpy数组中的每个元素都和标量进行运算，其中会用到广播机制
由此可得：数组通过一些激活函数后，输出与输入形状一致

1.3.2 点积运算

即内积， numpy.dot(a, b, out=None)

1.4 数组变形

在矩阵或者数组的运算中，会遇到需要把多个向量或矩阵按某轴方向合并或展平（如在卷积或循环神经网络中，在全连接层之前，需要把矩阵展平）的情况。

1.4.1 更改数组的形状

reshape: 不修改向量本身

import numpy as np 
arr = np.arange(10)
print(arr)
print(arr.reshape(2, 5))
print(arr.reshape(5,-1))# 指定维度时可以只指定行数或列数，其他用-1代替
# reshape函数不支持指定函数或列数，所以-1在这里是必要的
1
2
3
4
5
6

resize: 修改向量本身
ravel:

import numpy as np 
arr = np.arange(6).reshape(2, -1)
print(arr)
print("按列优先展平")
print(arr.ravel('F'))  #ravel不会产生原数组的副本
print("按行优先展平")
print(arr.ravel())
print("arr并没有被改变，arr:\n", arr)

1
2
3
4
5
6
7
8
9

flatten：把矩阵转换为向量，这种需求经常出现在卷积网络与全连接层之间

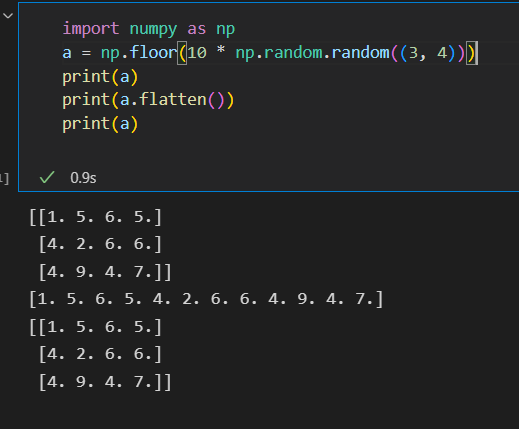
squeeze: 这是一个主要用来降维的函数，把矩阵中含1的维度去掉。在Pytorch中还有一种与之相反的操作—torch.unsqueeze
transpose: 对高维矩阵进行轴对换，这个在深度学习中经常使用，比如把图片中表示颜色顺序的RGB改为GBR(OpenCV默认通道为BGR，可能是基于某种硬件层面的原因。因为caffe，作为最早最流行的一批库的代表，用了opencv，而opencv默认通道是bgr的。这是opencv的入门大坑之一，bgr是个历史遗留问题，为了兼容早年的某些硬件)

import numpy as np 
arr2 = np.arange(24).reshape(2, 3, 4)
print(arr2.shape)
print(arr2.transpose(1, 2, 0).shape)    # 本来0, 1, 2的位置对调更换为1, 2, 0
1
2
3
4

1.4.2 合并数组

列举了常见的用于数组或向量合并的方法

1）append， concatenate以及stack都有一个axis参数， 用于控制数组的合并方式是按行还是按列
2）对于append和concatenate, 待合并的数组必须有相同的行数或列数（满足一个即可）
3）stack, hstack, dstack 要求待合并的数组必须具有相同的形状（shape）

1. append:

import numpy as np 
# 合并一维数组
a = np.array([1,2,3])
b = np.array([4,5,6])
c = np.append(a, b)
print(c)
# 合并多维数组
a = np.arange(4).reshape(2,2)
b = np.arange(4).reshape(2,2)
# 按行合并
c = np.append(a, b, axis=0)
print("按行合并后的结果")
print(c)
print('合并后数据维度', c.shape)
# 按列合并
d = np.append(a, b, axis=1)
print('按列合并后的结果')
print(d)
print('合并后数据维度', d.shape

################输出
[1 2 3 4 5 6]
按行合并后的结果
[[0 1]
 [2 3]
 [0 1]
 [2 3]]
合并后数据维度 (4, 2)
按列合并后的结果
[[0 1 0 1]
 [2 3 2 3]]
合并后数据维度 (2, 4)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

2. concatenate: 沿指定轴连接数组或矩阵
   
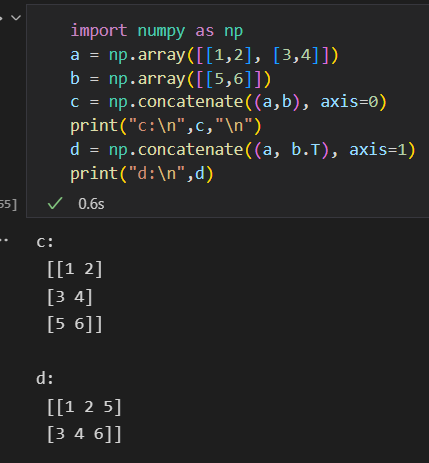
3. stack: 沿指定轴堆叠数组或矩阵
   

1.5 批量处理

把大数据拆分为多个批次的步骤：
1）得到数据集
2）随机打乱数据
3）定义批大小
4）批处理数据集

1.6 通用函数

Numpy提供了两种基本的对象，即ndarray和ufunc对象；
Numpy的另一个对象通用函数（ufunc）,ufunc是Universal Function的缩写，它是一种能对数组的每个元素进行操作的函数。计算速度快，比math模块中的函数更灵活。math模块的输入一般是标量，但Numpy中的函数可以是向量或矩阵，而利用向量或矩阵可以避免使用循环语句。


AttributeError module ‘time‘ has no attribute ‘clock’
原因是 Python3.8 不再支持time.clock，但在调用时依然包含该方法。
可以用 time.perf_counter() 来替换即可，然后可以正常使用计时

1. math与numpy函数的性能比较

import time 
import math 
import numpy as np 

x = [ i * 0.001 for i in np.arange(1000000)]
start = time.perf_counter()
for i, t in enumerate(x):
    x[i] = math.sin(t)
print("math.sin:", time.perf_counter() - start)

x = [i * 0.001 for i in np.arange(1000000)]
x = np.array(x)
start = time.perf_counter()
np.sin(x)
print("numpy.sin:",time.perf_counter() - start)
# 由此可见numpy.sin比math.sin快近10倍

#################
math.sin: 0.16589058306999505
numpy.sin: 0.010521452873945236
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

list和 array的区别：

2. 循环与向量运算比较
充分使用Python的numpy库中的内建函数（Built-in Function）,来实现计算的向量化，可大大提高运算速度。Numpy库中的内建函数使用了SIMD指令。使用向量化要比使用循环计算速度快得多。如果使用GPU，其性能将更强大，不过Numpy不支持GPU。PyTorch支持GPU。

import time 
import numpy as np 

x1 = np.random.rand(1000000)
x2 = np.random.rand(1000000)
# 使用循环计算向量点积
tic = time.process_time()
dot = 0
for i in range(len(x1)):
    dot += x1[i] * x2[i]
toc = time.process_time()
print("dot = " + str(dot) + "\n loop   ---time = " +
str(1000*(toc-tic)) + "ms")
 
# 使用numpy函数求点积
tic = time.process_time()
dot = 0
dot = np.dot(x1, x2)
toc = time.process_time()
print("dot = " + str(dot) + "\n verctor ---time = " + 
str(1000*(toc-tic)) + "ms")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

输出结果：
dot = 249904.11401943976
loop —time = 262.6966889999984ms
dot = 249904.11401943566
verctor —time = 5.148319999999984ms

因此在深度学习算法中，一般都使用向量化矩阵进行运算

1.7 广播机制

Numpy的universal functions中要求输入的数组shape是一致的，当数组的shape不相等时，则会使用广播机制。不过，调整数组使得shape一样，需要满足一定的规则，否则将出错。
规则如下：
1）让所有输入数组都向其中shape最长的数组看齐，不足的部分则通过在前面加1补齐，如：
a: 232
b:32
则b向a看齐，在b的前面加1，变成：13*2
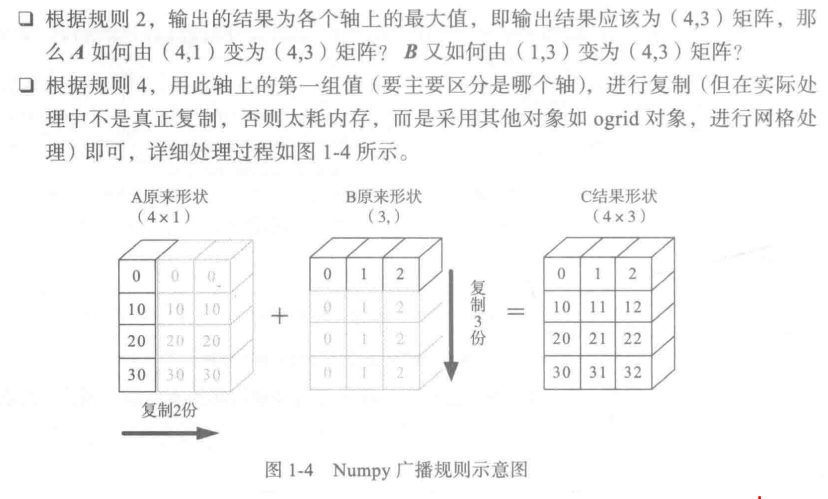
2) 输出数组的shape是输入数组shape的各个轴上的最大值；
3）如果输入数组的某个轴和输出数组的对应轴的长度相同或者某个轴的长度为1时，这个数组能被用来计算，否则出错；
4）当输入数组的某个轴的长度为1时，沿着此轴运算时都用（或复制）此轴上的第一组值



Numpy官网

第2章 Pytorch基础

pytorch是一个建立在Torch库之上的Python包，旨在加速深度学习应用。它提供一种类似Numpy的抽象方法来表征张量，可以利用GPU加速训练，采用动态计算图（Dynamic Computational Graph）结构，且基于tape的Autograd系统的深度神经网络。其他很多框架，比如TF(TF2.0也加入了动态网络的支持)， Caffe, CNTK, Theano等，采用静态计算图。

Numpy与Tensor

Tensor自称为神经网络界的Numpy，它与Numpy相似，二者可以共享内存，且之间的转换非常方便和高效。
不同：Numpy会把ndarray放在CPU中进行加速，而Torch产生的Tensor会放在GPU中进行加速运算（假设当前环境有GPU）

2.4.1 Tensor概述

对Tensor的操作很多，从接口的角度可分两类：
1）torch.function, 如torch.sum, torch.add等
2）tensor.function, 如tensor.view, tensor.add等
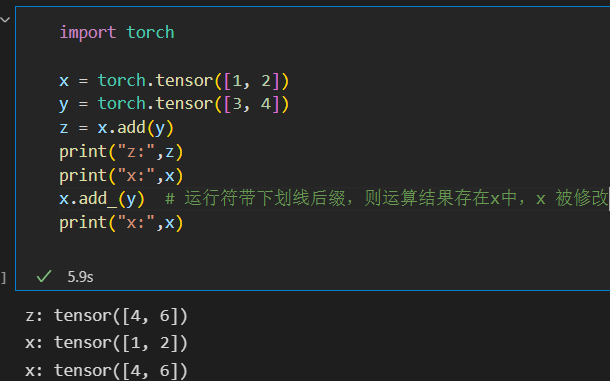
这些操作对于大部分的Tensor都是等价的，如torch.add(x, y)与x.add(y)等价

从修改方式的角度也可分为两类：
1）不修改自身数据，如x.add(y), x的数据不变，返回一个新的Tensor
2）修改自身数据，如x.add_(y)(运行符带下划线后缀)，运算结果存在x中，x被修改

2.4.2 创建Tensor

可以从列表或ndarray等类型进行构建，也可根据指定形状构建

import torch 
# 根据list数据生成Tensor 
print("list->Tensor:\n",torch.Tensor([1, 2, 3, 4, 5, 6]))
# 根据指定形状生成Tensor
print("\n2*3 Tensor:\n",torch.Tensor(2, 3))
# 根据给定的Tensor的形状
t = torch.Tensor([[1, 2, 3],[4, 5, 6]])
# 查看Tensor的形状
print("\nt.size():\n",t.size())
# shape与size()等价方式
print("\nt.shape:\n",t.shape)
#根据已有形状创建Tensor
print("\nt.size()->Tensor:\n",torch.Tensor(t.size()))
1
2
3
4
5
6
7
8
9
10
11
12
13

【说明】
torch.Tensor和torch.tensor的几点区别：
1）torch.Tensor是torch.empty和torch.tensor之间的一种混合，但是，当传入数据时，torch.Tensor使用全局默认dtype(FloatTensor),而torch.tensor是从数据中推断数据类型
2）torch.tensor(1)返回一个固定值1，而torch.Tensor(1)返回一个大小为1 的张量，它是随机初始化的值

import torch 

t1 = torch.Tensor(1)  # 返回一个大小为1的张量，随机初始化的值
t2 = torch.tensor(1) #返回固定值1 
print("t1的值{}, t1的数据类型{}".format(t1, t1.type()))
print("t2的值{}, t2的数据类型{}".format(t2, t2.type()))
1
2
3
4
5
6

t1的值tensor([1.4013e-45]), t1的数据类型torch.FloatTensor
t2的值1, t2的数据类型torch.LongTensor

【rand和randn的区别：】
rand: rand 生成均匀分布的伪随机数。分布在（0~1）之间
randn: 生成标准正态分布的伪随机数（均值为0，方差为1）
【size()和shape的区别：】
在numpy里面，两个是不相同的，size: 所有元素的个数和， shape: 数组类型大小（3，2） ，但在pytorch里面，两个是一样的,表达的都是数组类型

import torch
import numpy as np

a = np.array([[1,2,3],
              [4,5,6]])

x = torch.tensor(a)
print("numpy:")
print("Shape of a:",a.shape)
print("Type of a.shape:", type(a.shape))
print("Size of a:", a.size)
print("-------------")
print("pytorch:")
print("Shape of x:",x.shape)
print("Size of x:",x.size())
print("Type of x.size():",type(x.size()))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2.4.3 修改Tensor形状

import torch 
x = torch.randn(2, 3) # 2维， 2*3 
print(x.size())
print(x.dim())
print(x)
print(x.view(3,2))  #是先把x展平，然后在变为3*2???
y = x.view(-1)  # 把x展平为1维向量
print(y)
print("y.shape: ",y.shape)
#添加一个维度
z = torch.unsqueeze(y, 0)
print(z)
# 查看z的形状
print(z.size())
# 计算z 的元素个数
print(z.numel())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

【说明】：
torch.view和torch.reshape的异同：
1）reshape()可以由torch.reshape()， 也可由torch.Tensor.reshape()调用。但view()值可由torch.Tensor.view()调用
2）对于一个将要被view的Tensor, 新的size必须与原来的size与stride兼容。否则，在view之前必须调用contiguous()方法
3）同样也是返回与input数据量相同，但形状不同的Tensor。若满足view条件，则不会copy, 若不满足，则会copy
4) 如果指向重塑张量，请使用torch.reshape 如果还关注内存使用情况并希望确保两个张量共享相同的数据，请使用torch.view

2.4.4 索引操作

在pytorch中,gather()函数的作用是将数据从input中按index提出,
scatter_(input, dim, index, src): 将src中数据根据index中的索引按照dim的方向填进input。可以理解成放置元素或者修改元素
dim：沿着哪个维度进行索引
index：用来 scatter 的元素索引
src：用来 scatter 的源元素，可以是一个标量或一个张量

2.4.5广播机制

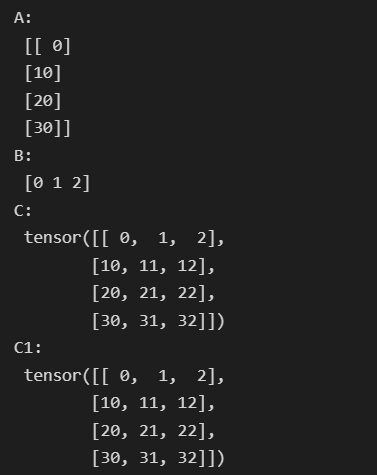
pytorch支持自动广播，torch.from_numpy(A)

import torch 
import numpy as np 

A = np.arange(0, 40, 10).reshape(4,1)  # A为2维，即4*1矩阵
B = np.arange(0, 3)
# print("A:\n",A)
# print("B:\n",B)
# 把ndarray转换为Tensor
A1 = torch.from_numpy(A)  #形状为4*1
B1 = torch.from_numpy(B)  #形状为3
# Tensor自动实现广播
C = A1 + B1 
print("C:\n",C)
# 我们可以根据广播机制，手动进行配置
B2 = B1.unsqueeze(0)  # B2的形状为1*3 
# 使用expand函数重复数组，分别的4*3的矩阵
A2 = A1.expand(4, 3)
B2 = B1.expand(4, 3)
C1 = A2 + B2 
print("C1:\n", C1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

2.4.6 逐元素操作

2.4.7 归并操作

归并操作可用对整个Tensor，也可以沿着某个纬度进行归并，这类操作的输入输出形状一般并不相同，而是往往输入大于输出形状

【说明】：
归并操作一般涉及一个dim参数，指定沿哪个维进行归并。另一个参数是keepdim, 说明输出结果中是否保留维度1， 缺省情况是False, 即不保留

import torch 
a = torch.linspace(0, 10, 6)
print(a)
a = a.view((2,3))
print(a)
# 沿y轴方向累加，即dim=0
print(a.sum(dim=0))   #形状为[3]
# 沿y轴方向累加，即dim=0, 并保留含1的维度
print(a.sum(dim=0, keepdim=True))#形状为[1, 3]
1
2
3
4
5
6
7
8
9

2.4.8 比较操作

2.4.9 矩阵操作

2.4.10 Pytorch与Numpy比较

2.5 Tensor与Autograd

2.5.1 自动求导要点

为实现对Tensor自动求导，需考虑如下事项：
1）创建叶子结点的Tensor, 使用requires_grad参数指定是否记录对其的操作，以便之后利用backward()方法进行梯度求解。requires_grad参数的缺省值为False,如果要对其求导需设置为True, 然后与之有依赖关系的结点会自动变为True
2）可利用requires_grad_()方法修改Tensor的requires_grad属性。可以调用.detach()或者with torch.no_grad()：， 将不再计算张量的梯度，不再跟踪张量的历史记录。这点在评估模型，测试模型阶段中常常用到
3）通过运算创建的Tensor（即非叶子结点），会自动被赋予grad_fn属性。该属性表示梯度函数。叶子结点的grad_fn为None
4）最后得到的Tensor执行backward()函数，此时自动计算各变量的梯度，并将累加结果保存到grad属性中。计算完成后，非叶子结点的梯度自动释放
5）backward()函数接受参数，此参数应和调用backward()函数的Tensor的维度相同，或者是可broadcast的维度。如果求导的Tensor为标量（即一个数字），则backward中的参数可省略
6）反向传播的中间缓存会被清空，如果需要进行多次反向传播，需要指定backward中的参数retain_graph = True。多次反向传播时，梯度是累加的
7）非叶子结点的梯度backward调用后即被清空
8）可以通过用torch.no_grad()包裹代码块的形式来组织autograd去跟踪那些标记为.requesgrad=True的张量的历史记录。这步在测试阶段经常使用

在整个过程中, pytorch采用计算图的形式进行组织，该计算图为动态图，且在每次前向传播时，将重新构建。

深度学习中的梯度
深度学习中的梯度 梯度是一个向量,是一个n元函数f关于n个变量的偏导数,梯度会指向各点处的函数值降低的方向。更严格的讲,梯度指示的方向是各 点处的函数值减少最多的方向。

2.5.3 标量反向传播

PyTorch调用backward()方法，将自动计算各节点的梯度，这是一个反向传播过程


pytorch中retain_graph=True的作用：

总的来说进行一次backward之后，各个节点的值会清除，这样进行第二次backward会报错，如果加上retain_graph==True后,可以再来一次backward。
retain_graph如果设置为False，计算图中的中间变量在计算完后就会被释放。但是在平时的使用中这个参数默认都为False从而提高效率，和creat_graph的值一样

例子理解：假设有一个输入$x$, $y=x^2$, $z=y\ast 4$，然后有两个输出，一个output1 = z.mean(), 另一个output2 = z.sum(), 对这两个output执行backward

import torch 
x = torch.randn((1, 4), dtype=torch.float32, requires_grad=True)
y = x ** 2
z = y*4 
print(x, y, z)
loss1 = z.mean()
loss2 = z.sum()
print(loss1, loss2)
loss1.backward() #因为这里loss1为标量，所以无须给backward传参
print(loss1, loss2)
loss2.backward()
1
2
3
4
5
6
7
8
9
10
11

程序正常执行到第12行，所有的变量正常保存。但是在第13行报错：

RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.

分析：计算节点数值保存了，但是计算图x-y-z结构被释放了，而计算loss2的backward仍然试图利用x-y-z的结构，因此会报错。

因此需要retain_graph参数为True去保留中间参数从而两个loss的backward()不会相互影响。正确的代码应当把第11行以及之后改成

#假设需要执行两次backward,先执行第一个backward,再执行第二个backward
loss1 = backward(retain_graph=True)
loss2.backward() #执行完这个后，所有中间变量都会被释放，以便下一次的循环
1
2
3

retain_graph参考

叶子结点的梯度，如果没有设置requires_grad=True则执行backward后，其梯度为None
非叶子节点的梯度，执行backward之后，会自动清空

2.5.4 非标量反向传播

PyTorch有个简单的规定，不让张量（Tensor）对张量求导，只允许标量对张量求导，因此，如果目标张量对一个非标量调用backward(), 则需要传入一个gradient参数，该参数也是张量，而且需要与调用backward()的张量形状相同。传入此参数是为了把张量对张量的求导转换为标量对张量的求导

backward函数的格式为：
backward(gradient=None, retain_graph=None, create_graph=False)



记得对x的梯度清零！！！
上面backward之后得到的结果为$J^T$的原因如下：
结果y是一个向量，直接对y进行反向传播：
$\frac{\partial y}{\partial x_1}=\frac{\partial y}{\partial y_1}\frac{\partial y_1}{\partial x_1}+\frac{\partial y}{\partial y_2}\frac{\partial y_2}{\partial x_1}$
$\frac{\partial y}{\partial x_2}=\frac{\partial y}{\partial y_1}\frac{\partial y_1}{\partial x_2}+\frac{\partial y}{\partial y_2}\frac{\partial y_2}{\partial x_2}$
写成矩阵运算形式则如下：
[ ∂ y ∂ x 1 ∂ y ∂ x 2 ] = [ ∂ y 1 ∂ x 1 ∂ y 2 ∂ x 1 ∂ y 1 ∂ x 2 ∂ y 2 ∂ x 2 ] [ ∂ y ∂ y 1 ∂ y ∂ y 2 ] \left[

\right]=\left[\right]\left[\right] [∂x1∂y​∂x2∂y​​]=[∂x1​∂y1​​∂x2​∂y1​​​∂x1​∂y2​​∂x2​∂y2​​​][∂y1​∂y​∂y2​∂y​​]
可以看到，矩阵运算形式中前面2 × 2 的矩阵中的结果正是我们想要的。我们称之为雅可比(Jacobian)矩阵(严格地说，是雅可比矩阵的转置)。

由此可得backward之后得到的结果为$J^T$的原因。

pytorch中backward得到的雅克比矩阵为什么是转置后的？
在PyTorch中，只能对标量使用backward，如果对向量进行backward则会报错

import torch

x=torch.tensor([2,3,4],dtype=torch.float,requires_grad=True)
print(x)
y=x*2
print(y)
# z=y.mean()
# z.backward()
y.backward()
print(x.requires_grad)
print(x.grad)
1
2
3
4
5
6
7
8
9
10
11

以上代码运行：RuntimeError: grad can be implicitly created only for scalar outputs
但如果我们将y.backward()改为y.backward(torch.Tensor([1,1,1]))，则可以正确输出x的梯度。

可以看到，矩阵运算形式中前面2 × 2的矩阵中的结果正是我们想要的。我们称之为雅可比(Jacobian)矩阵(严格地说，是雅可比矩阵的转置)。

这正是pytorch官方文档中所说的思想。当我们对向量进行反向传播时，通过在backward()中添加一个向量v vv，就可以分别得到原向量中每一项乘向量v vv中系数后对应的梯度值。

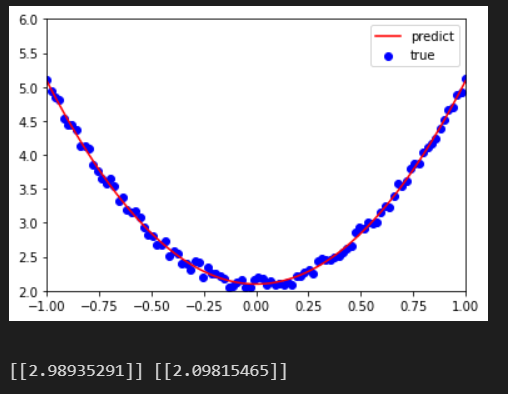
2.6 使用numpy实现机器学习

# y = 3*x*x +2
# 1)导入需要的库
import numpy as np 
from matplotlib import pyplot as plt 
#2)生成输入数据x以及目标数据y
#设置随机数种子，生成同一个份数据，以便用多种方法进行比较
np.random.seed(100)
x = np.linspace(-1, 1, 100).reshape(100,1)
y = 3*np.power(x, 2) + 2 + 0.2*np.random.rand(x.size).reshape(100,1)
#3)查看x,y数据分布情况
plt.scatter(x,y)
plt.show()

# 4)初始化权重参数
w1 = np.random.rand(1, 1)
b1 = np.random.rand(1, 1)
# 5) 训练模型
lr = 0.001  #learning rate学习率
for i in range(800):
    # 前向传播
    y_pred = np.power(x, 2)*w1 + b1
    # 定义损失函数
    loss = 0.5*(y_pred -y) ** 2
    loss = loss.sum()
    #计算梯度
    grad_w = np.sum((y_pred - y) * np.power(x, 2))
    grad_b = np.sum(y_pred -y)
    #使用梯度下降法，使得loss最小
    w1 -= lr * grad_w
    b1 -= lr * grad_b

# 6) 可视化结果
plt.plot(x, y_pred, 'r-', label='predict') #绘制经过点的曲线
plt.scatter(x, y, color='blue',marker='o', label='true')#绘制散点图
plt.xlim(-1, 1) #显示x轴的作图范围
plt.ylim(2, 6)  #显示y轴的作图范围
plt.legend()# 显示图例
plt.show()
print(w1, b1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

2.7 使用Tensor及Antograd实现机器学习

此处将使用Pytorch的一个自动求导的包----antograd, 利用这个包以及对应的Tensor，便可利用自动反向传播来求梯度，无需手工计算梯度。

# 1) 导入需要的库
import torch as t 
from matplotlib import pyplot as plt 
# 2) 生成训练数据，并可视化数据分布情况
t.manual_seed(100)
dtype = t.float
# 生成x坐标数据，x为tensor,需要把x的形状转换为100*1
x = t.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
# 生成y坐标数据，y为tensor,形状为100*1，另加上一些噪声
y = 3 * x.pow(2) + 2 + 0.2*torch.rand(x.size())

# 画图，把tensor数据转换为numpy数据
plt.scatter(x.numpy(), y.numpy())
plt.show



# 3）初始化权重参数
# 随机初始化参数，参数w,b为需要学习的，故需requires_grad=True
w = t.randn(1, 1, dtype=dtype, requires_grad=True)
b = t.zeros(1, 1, dtype=dtype, requires_grad=True)

# 4) 训练模型
lr = 0.001   #学习率
for ii in range(800):
    # 前向传播，并定义损失函数loss
    y_pred = x.pow(2).mm(w) + b
    loss = 0.5 * (y_pred - y) ** 2
    loss = loss.sum()

    # 自动计算梯度，梯度存放在grad属性中
    loss.backward()

    # 手动更新参数，需要用torch.no_grad(),使上下文环境中切断自动求导的计算
    with t.no_grad():
        w -= lr * w.grad
        b -= lr * b.grad
        # 梯度清零
        w.grad.zero_()
        b.grad.zero_()

# 5) 可视化训练结果
plt.plot(x.numpy(), y_pred.detach().numpy(), 'r-', label='predict')
plt.scatter(x.numpy(), y.numpy(), color='blue', marker='o', label='true')

plt.xlim(-1, 1)
plt.ylim(2, 6)
plt.legend()
plt.show()
print(w, b)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50