遗传算法GA求解连续函数问题

目录

一、遗传算法基本思想

二、遗传算法的主要步骤

三、遗传编码

1.二进制编码

2.实数编码

四、遗传算法流程

五、例题

---

一、遗传算法基本思想

遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。

二、遗传算法的主要步骤

（1）编码：将问题的候选解用染色体表示，实现解空间向编码空间的映射过程。遗传算法不直接处理解空间的决策变量，而是将其转换成由基因按一定结构组成的染色体。编码方式有很多，如二进制编码、实数向量编码、整数排列编码、通用数据结构编码等等。本文将采用二进制编码的方式，将十进制的变量转换成二进制，用0和1组成的数字串模拟染色体，可以很方便地实现基因交叉、变异等操作。 

（2）种群初始化：产生代表问题可能潜在解集的一个初始群体（编码集合）。种群规模设定主要有以下方面的考虑：从群体多样性方面考虑，群体越大越好，避免陷入局部最优；从计算效率方面考虑，群体规模越大将导致计算量的增加。应该根据实际问题确定种群的规模。产生初始化种群的方法通常有两种：一是完全随机的方法产生；二是根据先验知识设定一组必须满足的条件，然后根据这些条件生成初始样本。

（3）计算个体适应度：利用适应度函数计算各个个体的适应度大小。适应度函数（Fitness Function）的选取直接影响到遗传算法的收敛速度以及能否找到最优解，因为在进化搜索中基本不利用外部信息，仅以适应度函数为依据，利用种群每个个体的适应程度来指导搜索。

（4）进化计算：通过选择、交叉、变异，产生出代表新的解集的群体。选择（selection）：根据个体适应度大小，按照优胜劣汰的原则，淘汰不合理的个体；交叉（crossover）：编码的交叉重组，类似于染色体的交叉重组；变异（mutation）：编码按小概率扰动产生的变化，类似于基因突变。

（5）解码：末代种群中的最优个体经过解码实现从编码空间向解空间的映射，可以作为问题的近似最优解。这是整个遗传算法的最后一步，经过若干次的进化过程，种群中适应度最高的个体代表问题的最优解，但这个最优解还是一个由0和1组成的数字串，要将它转换成十进制才能供我们理解和使用。

三、遗传编码

遗传编码将变量转化为基因组的表示形式，优化变量的编码机制有二进制编码、十进制编码（实数编码）等。

1.二进制编码

这里简单介绍以下二进制编码的实现原理。例如，求实数区间上函数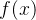的最大值，传统的方法是不断调整自变量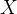的值，假设使用二进制编码新式，我们可以由长度6的未穿表示变量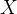，即从000000到111111，并将中间的取值映射到实数区间内。由于哦才能够整数上来看，6位长度二进制表示范围为0~63，所以对应的区间，每个相邻值之间的阶跃值为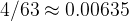。这个就是编码的精度，编码精度越高，所得到的解的质量也越高。

2.实数编码

在解决高维、连续优化问题等是，经常采用实数编码方式。实数编码的优点是计算精度搞，便于和经典连续优化算法结合。

四、遗传算法流程

1）初始化。设置进化代数计数器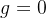，设置最大进化代数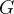，随机生成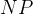个个体作为初始群体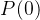

2）个体评价。计算群体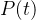中各个个体的适应度

3）选择运算。将选择算子作用域群体，根据个体适应度，按照一定的规则和方法，选择一些优良个体遗传到下一代群体。

4）交叉运算。将交叉算子作用于群体，对选中的成对个体，以某一概率交换他们之间的部分染色体，产生新的个体

5）变异运算。将变异算子作用于群体，对选中的个体，以某一概率改变某一个或某一些基因值为其他的等位基因。群体P(t)经过选择、交叉、和变异运算之后得到下一代群体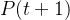。计算其适应度值，并根据适应度值进行排序，准备进行下一代遗传操作。

6）终止条件判断：若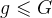，则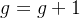，转到步骤2）；若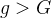，则终止计算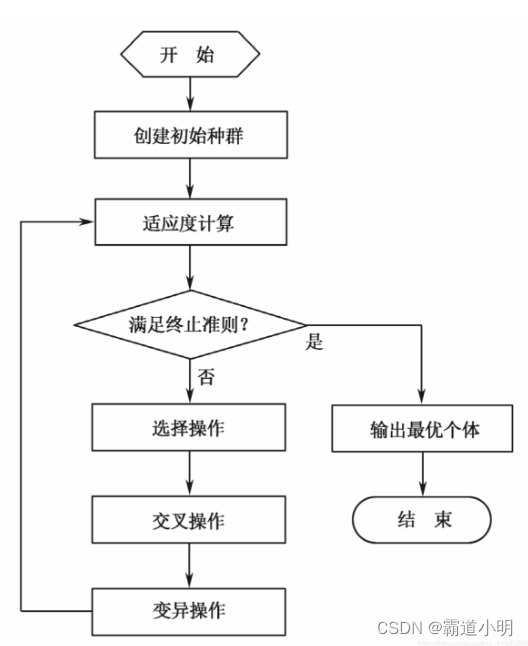

五、例题

用标准遗传算法求函数的最大值，其中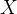的取值范围为 。函数图像图下

仿真过程如下：

1）初始化种群数目NP=50，染色体二进制编码长度为L=20，最大进化代数G=100，交叉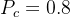概率，变异概率 。

2）产生初始化种群，将二进制编码转换成十进制，计算个体适应度值，并进行归一化；采用基于轮盘赌的选择操作，基于概率的交叉和变异操作，产生新的种群，并把历代最优个体保留在新种群中，进行下一步遗传操作

3）判断是否满足条件：若满足，则结束搜索

%%%%%%%%%%%%%%%%%%%%标准遗传算法求函数极值%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%初始化参数%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;              %清除所有变量
close all;              %清图
clc;                    %清屏
NP=50;                  %种群数量
L=20;                   %二进制数串长度
Pc=0.8;                 %交叉率
Pm=0.1;                 %变异率
G=100;                  %最大遗传代数
Xs=10;                  %上限
Xx=0;                   %下限
f=randi([0,1],NP,L);        %随机获得初始种群
%%%%%%%%%%%%%%%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%%%%%%%%%%
for k=1:G
    %%%%%%%%%%%%将二进制解码为定义域范围内十进制%%%%%%%%%%%%%%
    for i=1:NP
        U=f(i,:);
        m=0;
        for j=1:L
            m=U(j)*2^(j-1)+m;
        end
        x(i)=Xx+m*(Xs-Xx)/(2^L-1);
        Fit(i)= func1(x(i));
    end
    maxFit=max(Fit);           %最大值
    minFit=min(Fit);           %最小值
    rr=find(Fit==maxFit);
    fBest=f(rr(1,1),:);        %历代最优个体   
    xBest=x(rr(1,1));
    Fit=(Fit-minFit)/(maxFit-minFit);  %归一化适应度值
    %%%%%%%%%%%%%%%%%%基于轮盘赌的复制操作%%%%%%%%%%%%%%%%%%%
    sum_Fit=sum(Fit);
    fitvalue=Fit./sum_Fit;
    fitvalue=cumsum(fitvalue);
    ms=sort(rand(NP,1));
    fiti=1;
    newi=1;
    while newi<=NP
        if (ms(newi))<fitvalue(fiti)
            nf(newi,:)=f(fiti,:);
            newi=newi+1;
        else
            fiti=fiti+1;
        end
    end   
    %%%%%%%%%%%%%%%%%%%%%%基于概率的交叉操作%%%%%%%%%%%%%%%%%%
    for i=1:2:NP
        p=rand;
        if p<Pc
            q=randi([0,1],1,L);
            for j=1:L
                if q(j)==1;
                    temp=nf(i+1,j);
                    nf(i+1,j)=nf(i,j);
                    nf(i,j)=temp;
                end
            end
        end
    end
    %%%%%%%%%%%%%%%%%%%基于概率的变异操作%%%%%%%%%%%%%%%%%%%%%%%
    i=1;
    while i<=round(NP*Pm)
        h=randi([1,NP],1,1);      %随机选取一个需要变异的染色体
        for j=1:round(L*Pm)         
            g=randi([1,L],1,1);   %随机需要变异的基因数
            nf(h,g)=~nf(h,g);
        end
        i=i+1;
    end
    f=nf;
    f(1,:)=fBest;                   %保留最优个体在新种群中
    trace(k)=maxFit;                %历代最优适应度
end
xBest;                              %最优个体
figure
plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
%%%%%%%%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function result=func1(x)
fit= x+10*sin(5*x)+7*cos(4*x);
result=fit;
end