【数论】卡特兰数

知识点

---

一 . 进出栈问题

例题：洛谷 P1044 [NOIP2003 普及组] 栈

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

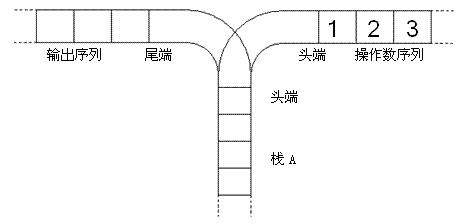
宁宁考虑的是这样一个问题：一个操作数序列，（图示为 1 到 3 的情况），栈 A 的深度大于 n。

现在可以进行两种操作，

1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1的过程。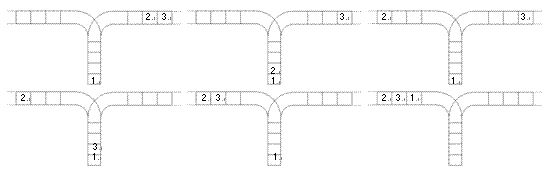

（原始状态如上图所示）

你的程序将对给定的 n，计算并输出由操作数序列 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 。

输出格式

输出文件只有一行，即可能输出序列的总数目。

输入输出样例

输入 #1

3

输出 #1

5

说明/提示

【题目来源】

NOIP 2003 普及组第三题

 方法1：记忆化搜索

#include 
#include 
using namespace std;
int stack[100][100];
int n;
int dfs(int x,int y)
{
	if(x==0)	return 1;
	if(stack[x][y]!=0)	return stack[x][y];	
	if(y>0)	stack[x][y]+=dfs(x,y-1);
	stack[x][y]+=dfs(x-1,y+1);
	return stack[x][y];	
}
 
int main()
{
	cin>>n;
	cout<<dfs(n,0)<
	return 0;
}

 方法2：通过递推式进行运算

（待填坑）

方法3：卡特兰数公式（待填坑）

---

相关练习：洛谷 P1754 球迷购票问题

方法一：动态规划

思路：设dp[i][j]，下标表示已经有 i 张50元的纸币，有 j 张100元的纸币；在满足 的情况下，统计下一个人是50元的总情况数与下一个人是100元的总情况数之和，为当前时间的总情况数。

#include 
#include 
#include 
#include 
using namespace std;
int n;
int dp[105][105];
inline int read()
{
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9')
	{
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9')
	{
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
int main()
{
	n=read();
	for(int i=1;i<=n;++i)
	{
		dp[i][0]=1; //有i张50元的纸币，没有100元的总情况只有1种，进行初始化
	}
	for(int i=1;i<=n;++i)
	{
		for(int j=1;j<=i;++j) //100元的数目不能超过50元的纸币
		{
			dp[i][j]=dp[i-1][j]+dp[i][j-1]; 
        //下一轮的情况：下一个人是50元的总情况数与下一个人是100元的总情况数之和
		}
	}
	printf("%d",dp[n][n]);
	return 0;
}

方法二：卡特兰数公式