公式向-完美解释梯度消失与LSTM

前言

为了获取最佳阅读体验，建议访问个人博客：https://jmxgodlz.xyz

首先抛出关键性结论：

1. RNN模型在时间维度共享参数矩阵，因此RNN模型总的梯度等于各时间的梯度之和，$g=\sum g_t$。

2. RNN中总的梯度不会消失，只是远距离梯度消失，梯度被近距离梯度主导，无法捕获远距离特征。

3. 梯度消失的本质：由于RNN模型在时间维度共享参数矩阵，导致针对隐藏状态h求导时，循环计算矩阵乘法，最终梯度上出现了参数矩阵的累乘。

4. LSTM缓解梯度消失的本质：引入门控机制，将矩阵乘法转为逐元素相乘的哈达马积:$c_t=f_t\odot c_{t-1}+i_t\odot \tanh \left(W_c\left[h_{t-1},x_t\right]+b_c\right)$

梯度消失分析

基本介绍

RNN的状态更新公式如下：

h t = f ( W h t − 1 + U x t )

ht​=f(Wht−1​+Uxt​)​(1)​

$$y_t=f(V{h}_t)\text{\hspace{1em}(2)}$$

其中，h表示隐藏状态，f表示激活函数，W、U表示参数矩阵，x表示输入。从该式中可以看出不同时间维度的参数矩阵是共享的。

反向传播

我们在反向传播过程进行梯度求导，以对参数矩阵U求导为例

$$\frac{\partial y_t}{\partial U}=\frac{\partial y_t}{\partial h_t}\frac{\partial h_t}{\partial U}\text{\hspace{1em}(3)}$$

其中

∂ h t ∂ U = ∑ s = 0 t ∂ h t ∂ h s ∂ h s ∂ U

∂U∂ht​​=s=0∑t​∂hs​∂ht​​∂U∂hs​​​(4)​

$$\frac{\partial h_t}{\partial h_s}=\frac{\partial h_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial h_{t-2}}\dots \frac{\partial h_{s+1}}{\partial h_s}\text{\hspace{1em}(5)}$$

从式（1）（2）中可以递推到$h_0$，每一个隐藏状态h均与参数矩阵有关，最后的梯度$y_t$依赖于每一个隐藏状态。

$以y_2为例,y_2=f(V{h}_2)=f(Vf(W{h}_1+U{x}_1))=f(Vf(Wf(W{h}_0+U{x}_0)+U{x}_1))$,通过全微分求导，$h_t$对$U,h_{t-1}$求偏导数

∂ y 2 ∂ U = ∂ y 2 ∂ h 2 ∂ h 2 ∂ U = ∂ y 2 ∂ h 2 ( ∂ h 2 ∂ h 1 ∗ ∂ h 1 ∂ U + ∂ h 2 ∂ U ) = ∂ y 2 ∂ h 2 ( ∂ h 2 ∂ h 1 ∗ ( ∂ h 1 ∂ h 0 ∗ ∂ h 0 ∂ U + ∂ h 1 ∂ U ) + ∂ h 2 ∂ U ) = ∂ y 2 ∂ h 2 ( ∂ h 2 ∂ U + ∂ h 2 ∂ h 1 ∂ h 1 ∂ U + ∂ h 2 ∂ h 1 ∂ h 1 ∂ h 0 ∂ h 0 ∂ U ) (6)

\tag{6} ∂U∂y2​​​=∂h2​∂y2​​∂U∂h2​​=∂h2​∂y2​​(∂h1​∂h2​​∗∂U∂h1​​+∂U∂h2​​)=∂h2​∂y2​​(∂h1​∂h2​​∗(∂h0​∂h1​​∗∂U∂h0​​+∂U∂h1​​)+∂U∂h2​​)=∂h2​∂y2​​(∂U∂h2​​+∂h1​∂h2​​∂U∂h1​​+∂h1​∂h2​​∂h0​∂h1​​∂U∂h0​​)​(6)

$$设:z_t=W{h}_{t-1}+U{x}_t\text{\hspace{1em}(7)}$$

$z_t$代表未经过激活函数的神经网络输出，式（1）转化为：

$$h_t=f(z_t)\text{\hspace{1em}(8)}$$

$$\frac{\partial h_t}{\partial h_{t-1}}=\frac{\partial h_t}{\partial z_t}\frac{\partial z_t}{\partial h_{t-1}}\text{\hspace{1em}(9)}$$

式（8）可以拆分为两部分：

$$\frac{\partial z_t}{\partial h_{t-1}}=W\text{\hspace{1em}(10)}$$

∂ h t ∂ z t = ( ∂ h t , 1 ∂ z t , 1 ∂ h t , 1 ∂ z t , 2 ⋯ ∂ h t , 1 ∂ z t , n ⋮ ⋮ ⋱ ⋮ ∂ h t , n ∂ z t , 1 ∂ h t , n ∂ z t , 2 ⋯ ∂ h t , n ∂ z t , n ) (11) \frac{\partial h_{t}}{\partial z_{t}}=\left(

\right) \tag{11} ∂zt​∂ht​​=⎝ ⎛​∂zt,1​∂ht,1​​⋮∂zt,1​∂ht,n​​​∂zt,2​∂ht,1​​⋮∂zt,2​∂ht,n​​​⋯⋱⋯​∂zt,n​∂ht,1​​⋮∂zt,n​∂ht,n​​​⎠ ⎞​(11)

其中，$h_t$元素由$z_t$逐元素激活得到，因此两者对应元素才具有依赖关系，未对应元素无依赖关系，导数为0，式（10）成为一个对角矩阵.

∂ h t ∂ z t = ( f ′ (  z t , 1 ) 0 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ f ′ ( z t , n ) ) = d i a g [ f ′ ( z t ) ] (12) \frac{\partial h_{t}}{\partial z{t}}=\left(

\right)=diag[f^{\prime}(z_t)] \tag{12} ∂zt∂ht​​=⎝ ⎛​f′( zt,1​)⋮0​0⋮0​⋯⋱⋯​0⋮f′(zt,n​)​⎠ ⎞​=diag[f′(zt​)](12)

根据式（9）（11），式（5）求解得到：

$$\frac{\partial h_t}{\partial h_s}=\prod _{k=s+1}^t{W}^T\mathrm{diag}\left[f^{\prime }\left(z_k\right)\right]\text{\hspace{1em}(13)}$$

在式（12）中已经出现了矩阵的连乘，根据矩阵的相容性"$||XY||\le ||X||||Y||$"

∣ ∣ ∂ h t ∂ h s ∣ ∣ = ∏ k = s + 1 t ∣ ∣ W T diag ⁡ [ f ′ ( z ⁡ k ) ] ∣ ∣ ≤ ∏ k = s + 1 t ∣ ∣ W T ∣ ∣ ∣ ∣ diag ⁡ [ f ′ ( z ⁡ k ) ] ∣ ∣ ≤ ∏ k = s + 1 t σ m a x γ = ( σ m a x γ ) t − s (14)

\tag{14} ∣∣∂hs​∂ht​​∣∣​=k=s+1∏t​∣∣WTdiag[f′(zk​)]∣∣≤k=s+1∏t​∣∣WT∣∣∣∣diag[f′(zk​)]∣∣≤k=s+1∏t​σmax​γ=(σmax​γ)t−s​(14)

其中,$\sigma$ 代表矩阵W的最大奇异解，$\gamma$代表激活函数f的上界，例如双曲正切函数的上界为$||tan{h}^{{}^{\prime }}(x)||\le 1$，sigmoid函数的上界为$||sigmoi{d}^{{}^{\prime }}(x)\le \frac{1}{4}||$。
因此在远距离依赖，即t-s较大的情况下，当${\sigma }_{max}\gamma <1$时，会发生梯度消失;当${\sigma }_{max}\gamma >1$时，会发生梯度爆炸。

**TIPS：**这里只是不等式情况，因此即使不等式右边远大于1，也有可能发生梯度消失。但是，在实际情况下，矩阵范数的约束与实际值相当接近。

补充说明

对于传统RNN模型，在训练初期避免梯度消失与参数矩阵的初始化，即最大奇异解$\sigma$值有关。

避免梯度消失的矩阵最小初始化方式如下：

以双曲正切函数为例，双曲正切函数的$\gamma =1$，为了使${\sigma }_{max}\gamma =1$，即$\sigma =1$。

为了使不等式置信度更高，将矩阵W的所有奇异解设置为1.

对于每一列而言，${\Sigma }_i{w}_{ij}^2=1$，其中j代表第j列，矩阵中每个元素是一个n维向量，i代表矩阵第i行，w代表列向量。

$n\mathbb{E}\left(w^2\right)=1$，

我们假设w服从均匀分布，区间为$[-R,R]$,均匀分布的均值为0，方差$\mathbb{E}\left(w^2\right)=\frac{R^2}{3}$【均匀分布方差为$\frac{(b-a{)}^2}{12}$】。

代入得到$$n\frac{R^2}{3}=1\text{\hspace{1em}(15)}$$

即$$R=\frac{\sqrt{3}}{\sqrt{n}}\text{\hspace{1em}(16)}$$

因此w符合的分布为$[-\frac{\sqrt{3}}{\sqrt{n}},\frac{\sqrt{3}}{\sqrt{n}}]$，当矩阵是方阵时的Xavier-Glorot initialization分布；当矩阵行列不同时，Xavier-Glorot initialization分布为$\left[-\frac{\sqrt{6}}{\sqrt{m+n}},\frac{\sqrt{6}}{\sqrt{m+n}}\right]$。

LSTM提出

关于RNN反向传播的一些评论：

1. RNN模型在时间维度共享参数矩阵
2. 权重更新的频率与梯度的准确性需要权衡，越少的更新次数，梯度准确性越高，但训练速度也下降了。【由反向传递时，使用上一时刻状态做近似导致】
3. 梯度消失带来不稳定的梯度流；共享参数带来对最新更新的过度敏感
4. 针对上述三点，进行错误传播过程的梯度截断是有必要的
5. 传播梯度分量也是可以的

LSTM缓解梯度消失的根本方法：write it down【将状态记录下来】，但是如果无限制的写入也会带来问题，因此升级为有选择的读写，这样带来了LSTM的三个关键机制：

1. 有选择的写入，写入关键信息
2. 有选择的读取信息
3. 有选择的遗忘信息

我们可以通过门机制实现选择性，但要如何将这三个机制结合起来呢？

LSTM原型

首先，提出一个LSTM原型，本着先读取状态，再写入的原则，每一次更新状态的增量${\tilde{s}}_t$，由$o_t$选择性读取上一个状态的内容，$i_t$为选择写入，$f_t$选择性遗忘上一状态的内容：

i t = σ ( W i s t − 1 + U i x t + b i ) o t = σ ( W o s t − 1 + U o x t + b o ) f t = σ ( W f s t − 1 + U f x t + b f ) s t ~ = ϕ ( W ( o t ⊙ s t − 1 ) + U x t + b ) s t = f t ⊙ s t − 1 + i t ⊙ s ~ t (17)

\tag{17} it​ot​ft​st​~​st​​=σ(Wi​st−1​+Ui​xt​+bi​)=σ(Wo​st−1​+Uo​xt​+bo​)=σ(Wf​st−1​+Uf​xt​+bf​)=ϕ(W(ot​⊙st−1​)+Uxt​+b)=ft​⊙st−1​+it​⊙s~t​​(17)

三个起效果的改进版本

按理说上述LSTM原型能够起效果，但事与愿违，**选择性读取与选择性写入未能很好的协调，导致状态值非常大，紧接着门机制变得饱和。**这种情况源于的$s_t$是无界的，会变得非常大从而导致门机制饱和，因此接下来的三个改进的生效版本均是约束$s_t$的大小，将其约束成有界。

归一化LSTM原型

针对$s_t$进行正态归一化，$s_t=\frac{s_t-mean(s_t)}{\sqrt{Var(s_t)+1}}$，也可以类似于层归一化等方式添加缩放与平移分量。

归一化后的$s_t$从无界成为有界。

GRU：将写入与遗忘强绑定

$$s_t=\left(1-i_t\right)\odot s_{t-1}+i_t\odot {\tilde{s}}_t\text{\hspace{1em}(18)}$$

GRU将写入门与遗忘门绑定起来，使之加和为1。将$s_t$变成$s_{t-1}$与${\tilde{s}}_t$的element-wise加权平均，当两者均有界时，$s_t$也有界。

以下给出GRU的计算公式，与原理图：

r t = σ ( W r s t − 1 + U r x t + b r ) z t = σ ( W z s t − 1 + U z x t + b z ) s t ~ = ϕ ( W ( r t ⊙ s t − 1 ) + U x t + b ) s t = z t ⊙ s t − 1 + ( 1 − z t ) ⊙ s ~ t (19)

\tag{19} rt​zt​st​~​st​​=σ(Wr​st−1​+Ur​xt​+br​)=σ(Wz​st−1​+Uz​xt​+bz​)=ϕ(W(rt​⊙st−1​)+Uxt​+b)=zt​⊙st−1​+(1−zt​)⊙s~t​​(19)

伪LSTM：通过激活函数约束

通过激活函数，将$s_t$限制到激活函数的上界内。

只有在更新写入时，为了避免信息的变化，未使用激活函数约束。

以下给出伪LSTM的计算公式，与原理图：

i t = σ ( W i ( ϕ ( s t − 1 ) ) + U i x t + b i ) o t = σ ( W o ( ϕ ( s t − 1 ) ) + U o x t + b o ) f t = σ ( W f ( ϕ ( s t − 1 ) ) + U f x t + b f ) s ~ t = ϕ ( W ( o t ⊙ ϕ ( s t − 1 ) ) + U x t + b ) s t = f t ⊙ s t − 1 + i t ⊙ s ~ t r n n out  = ϕ ( s t ) (20)

\tag{20} it​ot​ft​s~t​st​rnnout ​​=σ(Wi​(ϕ(st−1​))+Ui​xt​+bi​)=σ(Wo​(ϕ(st−1​))+Uo​xt​+bo​)=σ(Wf​(ϕ(st−1​))+Uf​xt​+bf​)=ϕ(W(ot​⊙ϕ(st−1​))+Uxt​+b)=ft​⊙st−1​+it​⊙s~t​=ϕ(st​)​(20)

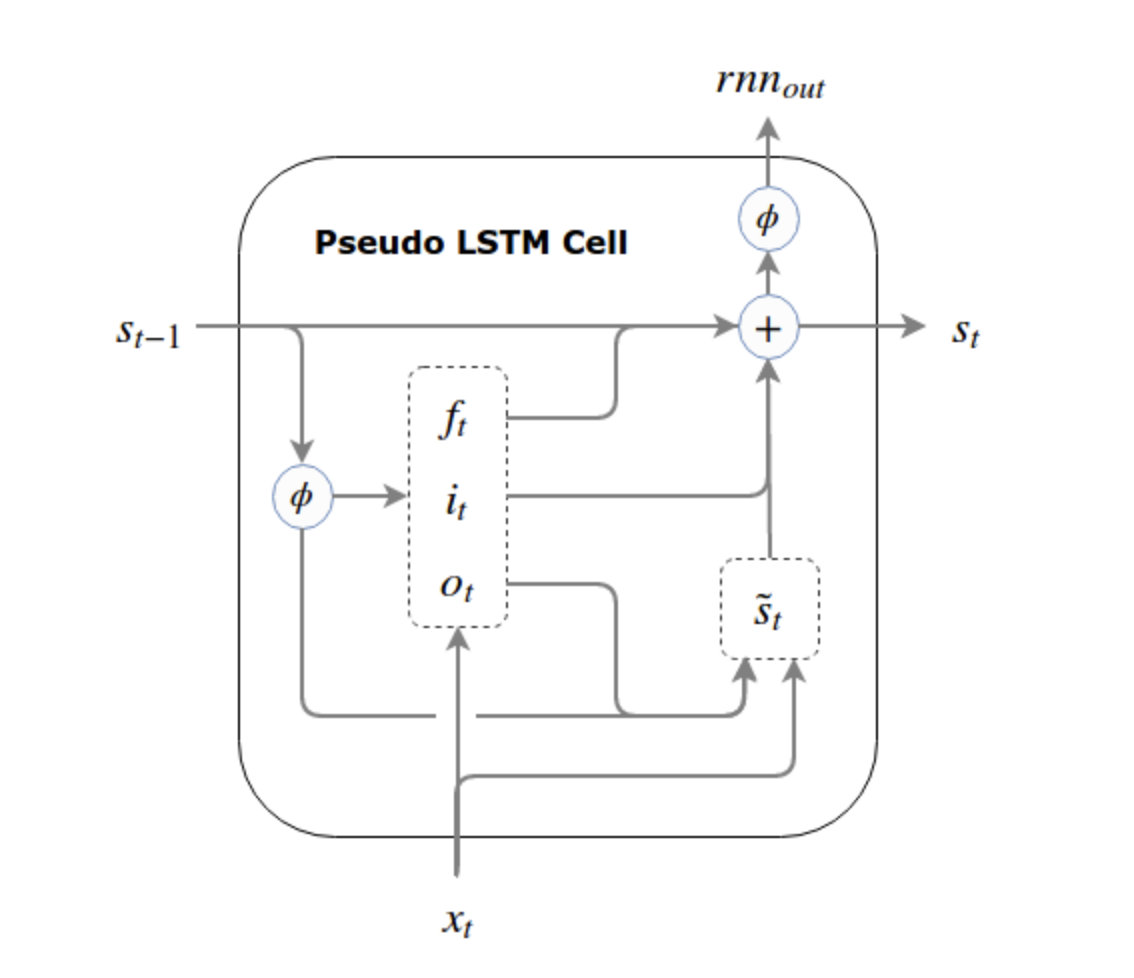
LSTM提出

LSTM与伪LSTM的几点关键区别如下：

1. LSTM是先写后读，因此添加了一个“影子”状态，Hochreiter and Schmidhuber等人认为状态s与剩余的RNN cell是独立的。

2. 使用门控影子状态$h_{t-1}=o_{t-1}\odot \varphi (c_{t-1})$计算门结构，替换激活后的$\varphi (c_{t-1})$。这样隐藏状态均是当前时间下的信息，与读取信息时$(o_t\odot s_{t-1})$利用前一时刻信息不同。

3. 使用门控影子状态作为RNN cell的输出$h_t=o_t\odot \varphi (c_t)$，替代$\varphi (c_t)$。

这样一来，LSTM的输入就是上一时刻的$c_{t-1},h_{t-1}$，输出为$c_t,h_t$。

基础LSTM

基础LSTM单元的公式与原理图如下：

i t = σ ( W i h t − 1 + U i x t + b i ) o t = σ ( W o h t − 1 + U o x t + b o ) f t = σ ( W f h t − 1 + U f x t + b f ) c ~ t = ϕ ( W h t − 1 + U x t + b ) c t = f t ⊙ c t − 1 + i t ⊙ c ~ t h t = o t ⊙ ϕ ( c t ) r n n out  = h t (21)

\tag{21} it​ot​ft​c~t​ct​ht​rnnout ​​=σ(Wi​ht−1​+Ui​xt​+bi​)=σ(Wo​ht−1​+Uo​xt​+bo​)=σ(Wf​ht−1​+Uf​xt​+bf​)=ϕ(Wht−1​+Uxt​+b)=ft​⊙ct−1​+it​⊙c~t​=ot​⊙ϕ(ct​)=ht​​(21)

The LSTM with peepholes

利用前一状态$c_{t-1}$来进行门控机制的计算，但输出利用实时信息$c_t$。

计算公式如下：

i t = σ ( W i h t − 1 + U i x t + P i c t − 1 + b i ) f t = σ ( W f h t − 1 + U f x t + P f c t − 1 + b f ) c ~ t = ϕ ( W h t − 1 + U x t + b ) c t = f t ⊙ c t − 1 + i t ⊙ c ~ t o t = σ ( W o h t − 1 + U o x t + P o c t + b o ) h t = o t ⊙ ϕ ( c t ) rnn ⁡ out  = h t (22)

\tag{22} it​ft​c~t​ct​ot​ht​rnnout ​​=σ(Wi​ht−1​+Ui​xt​+Pi​ct−1​+bi​)=σ(Wf​ht−1​+Uf​xt​+Pf​ct−1​+bf​)=ϕ(Wht−1​+Uxt​+b)=ft​⊙ct−1​+it​⊙c~t​=σ(Wo​ht−1​+Uo​xt​+Po​ct​+bo​)=ot​⊙ϕ(ct​)=ht​​(22)

LSTM如何解决梯度消失

从上述分析可以得到，梯度消失中最大原因是需要计算$\frac{\partial h_t}{\partial h_s}$，如果这个值不随着层数的增加，趋于0或者无穷大，那么就能够捕获到长距离依赖信息。

LSTM将状态与其他部分分开，状态更新部分变成:

$$c_t=f_t\odot c_{t-1}+i_t\ast {\tilde{c}}_t=c_t=f_t\odot c_{t-1}+i_t\odot \tanh \left(W_c\left[h_{t-1},x_t\right]+b_c\right)\text{\hspace{1em}(23)}$$

针对状态进行求导，同时$c_t$与$c_{t-1},{\tilde{c}}_{t-1},f_t,i_t$有关，因此进行全微分求导

∂ C t ∂ C t − 1 = ∂ C t ∂ C t − 1 + ∂ C t ∂ C ~ t ∗ ∂ C ~ t ∂ C t − 1 + ∂ C t ∂ i t ∗ ∂ i t ∂ C t − 1 + ∂ C t ∂ f t ∗ ∂ f t ∂ C t − 1 = ∂ C t ∂ C t − 1 + ∂ C t ∂ C ~ t ∗ ∂ C ~ t ∂ h t − 1 ∗ ∂ h t − 1 ∂ C t − 1 + ∂ C t ∂ i t ∗ ∂ i t ∂ h t − 1 ∗ ∂ h t − 1 ∂ C t − 1 + ∂ C t ∂ f t ∗ ∂ f t ∂ h t − 1 ∗ ∂ h t − 1 ∂ C t − 1 = f t + i t ∗ t a n h ′ ( ∗ ) W c ∗ o t − 1 t a n h ′ ( C t − 1 ) + C ~ t ∗ σ ′ ( ∗ ) W i ∗ o t − 1 t a n h ′ ( C t − 1 ) + C t − 1 ∗ σ ′ ( ∗ ) W f ∗ o t − 1 t a n h ′ ( C t − 1 ) (24)

\tag{24} ∂Ct−1​∂Ct​​​=∂Ct−1​∂Ct​​+∂C~t​∂Ct​​∗∂Ct−1​∂C~t​​+∂it​∂Ct​​∗∂Ct−1​∂it​​+∂ft​∂Ct​​∗∂Ct−1​∂ft​​=∂Ct−1​∂Ct​​+∂C~t​∂Ct​​∗∂ht−1​∂C~t​​∗∂Ct−1​∂ht−1​​+∂it​∂Ct​​∗∂ht−1​∂it​​∗∂Ct−1​∂ht−1​​+∂ft​∂Ct​​∗∂ht−1​∂ft​​∗∂Ct−1​∂ht−1​​=ft​+it​∗tanh′(∗)Wc​∗ot−1​tanh′(Ct−1​)+C~t​∗σ′(∗)Wi​∗ot−1​tanh′(Ct−1​)+Ct−1​∗σ′(∗)Wf​∗ot−1​tanh′(Ct−1​)​(24)

从上式可以得到，$\frac{\partial C_t}{\partial C_{t-1}}$成为上述4部分的加和，在连乘的任意时刻可能是$[0,+\infty )$的范围，并不会一直趋于0，或者$\infty$。同时$f_t,i_t,o_{t-1},{\tilde{C}}_t$都是网络学习的值，也就是说由网络自己学习哪些梯度保留，哪些梯度剔除。

在这些机制的帮助下，LSTM很好的缓解了梯度消失问题。

LSTM延伸

Highway网络和residual网络同样包含了LSTM最基本的思想：与原先一层网络输出$x_{t+1}=Net(x_t)$的计算方式相比，计算增量$x_{t+1}=x_t+\Delta x_{t+1}$。

因此这两种方式，同样会遇到LSTM的问题：读写的不协调。

关于这两者的介绍，再后续有时间展开进行介绍。

参考文献

https://www.zhihu.com/question/34878706

https://r2rt.com/written-memories-understanding-deriving-and-extending-the-lstm.html

https://www.zhihu.com/question/34878706

https://zhuanlan.zhihu.com/p/109519044

https://weberna.github.io/blog/2017/11/15/LSTM-Vanishing-Gradients.html?utm_source=wechat_session&utm_medium=social&utm_oi=1088177386838749184