一 问题描述

贝西正在玩方块游戏，方块编号为 1 到 N，开始时每个方块都相当于一个栈。贝西执行 P 个操作，操作类型有两种：M X Y，将包含 X 的栈整体移动到包含 Y 的栈顶部；C X，查询 X 方块下的方块数量。请统计贝西每个操作的结果。

二 输入和输出

1 输入

第 1 行为单个整数 P，表示操作的数量。第 2 到 P+1 行，每一行都描述一个操作。

2 输出

对每个 C 操作，都输出统计结果。

三 输入和输出样例

1 输入样例

6

M 1 6

C 1

M 2 4

M 2 6

C 3

C 4

2 输出样例

1

0

2

四 分析

本问题包括移动和计数两种操作，本问题可以借助并查集实现，在集合查找和合并时，更新树根下方的方块数量即可。使用并查集可以快速、高效地解决该问题。

五 算法设计

1 初始化

初始化每个方块的集合号都为其自身。

2 查询或者合并。

C X：查询 X 的集合号，并输出 X 方块下的方块数量。

d[i]：第 i 个方块下的方块数量。

查询 X 的祖宗，在返回过程中将经过路径上的节点的集合号统一为祖宗的集合号，将当前节点的 d 值加上其父节点的 d 值。

M X Y：合并 X、Y 集合号。

cnt[i]：第 i 个方块栈的方块数量。首先找到 X、Y 所在的集合 a、b，然后将 a 的集合号修改为 b，fa[a]=b,更新 d[a]=cnt[b],cnb[b]+=cnt[a]。

六 图解

1 初始化

fa[i]=i; // 方块 i 所属的集合号

d[i]=0; // 第 i 个方块下的方块数

cnt[i]=1; // 第 i 个栈的方块数

2 合并

M 1 6：将包含 1 的栈整体移动到包含 6 的栈。首先找到 1 和 6 的祖宗 1、6，然后将 1 的集合号修改为 6，fa[1]=6,更新 d[1]=cnt[6]=1,cnt[6]+=cnt[1]=2。

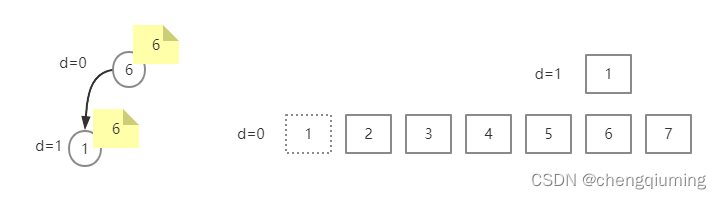
3 查询

C1：查询 1 下面有多少个方块。首先查询 1 的集合号，找祖宗，在查询过程中将当前节点 的 d 值加上其父节点的 d 值，d[1]=d[1]+d[6]=1。

4 合并

M 2 4：将包含 2 的栈整体移动到包含 4 的栈。首先找到 2 和 4 的祖宗 2、4，然后将 2 的集合号修改为 4，fa[2]=4,更新 d[2]=cnt[4]=1,cnt[4]=cnt[4]+cnt[2]=2。

5 合并

M 2 6：将包含 2 的栈整体移动到包含 6 的栈。首先找到 2 和 6 的祖宗 4、6，然后将 4 的集合号修改为 6，fa[4]=6，更新 d[4]=cnt[6]=2,cnt[6]=cnt[6]+cnt[4]=4。

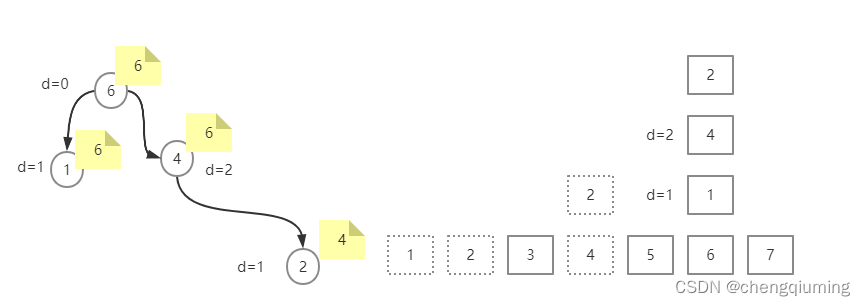
6 查询

C 3：查询 3 下面有多少个方块。首先查询 3 个集合号为 3，d[3]=0。

7 查询

C 4 ：查询 4 下面有多少个方块。首先查询 4 的集合号，在查询过程中将当前节点的集合号修改为其父节点的集合号，将当前节点的 d 值加上其父节点的 d 值，d[4]=d[4]+d[6]=2。

8 查询

C 2：查询 2 下面有多少个方块。先查询 2 的祖宗，在返回过程中将当前节点的 d 值加上其父节点 d 值，d[2]=d[2]+d[4]=3。

七 代码

package com.platform.modules.alg.alglib.poj1988;
 
public class Poj1988 {
    public String output = "";
 
    private final int N = 30010;
    int n;
    int fa[] = new int[N];
    int d[] = new int[N];
    int cnt[] = new int[N];
 
    void Init() {
        for (int i = 1; i < N; i++) {
            fa[i] = i;
            d[i] = 0;
            cnt[i] = 1;
        }
    }
 
    int Find(int x) {
        int fx = fa[x];
        if (x != fa[x]) {
            fa[x] = Find(fa[x]);
            d[x] += d[fx];
        }
        return fa[x];
    }
 
    void Union(int x, int y) {
        int a, b;
        a = Find(x);
        b = Find(y);
        fa[a] = b;
        d[a] = cnt[b];
        cnt[b] += cnt[a];
    }
 
    public String cal(String input) {
        String[] line = input.split("\n");
        n = Integer.parseInt(line[0]);
        Init();
        for (int count = 0; count < n; count++) {
            String[] words = line[count + 1].split(" ");
            if (words[0].charAt(0) == 'C') {
                int i = Integer.parseInt(words[1]);
                Find(i);
                output += "" + d[i] + "\n";
            } else {
                int i = Integer.parseInt(words[1]);
                int j = Integer.parseInt(words[2]);
                Union(i, j);
            }
        }
        return output;
    }
}

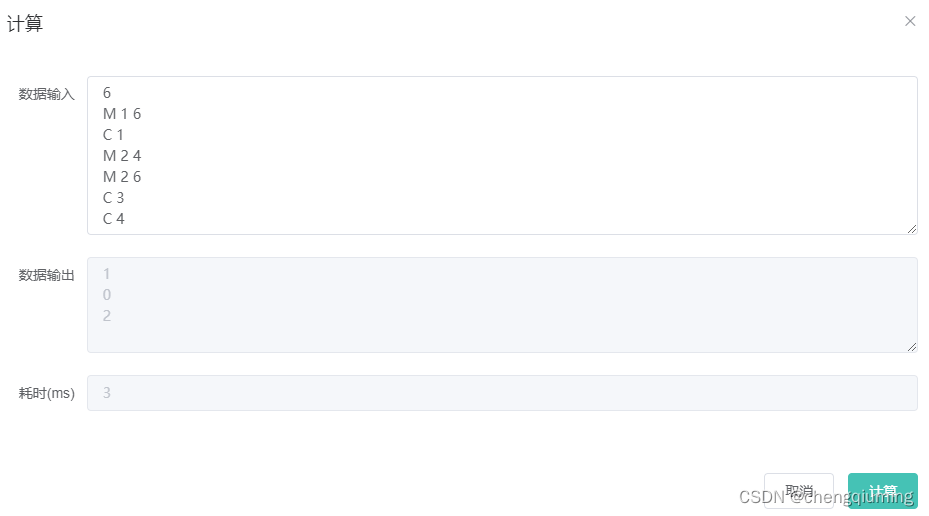
八  测试