自注意力机制（Self-attention）【第四章】

---

解决的问题

解决的问题：输入的向量不是单一向量，并且输入的 sequence 大小不固定。

应用领域

输入是句子（sequence）

输入是声音讯号

社交网络

一个分子

输出：有 3 种可能性

Sequence Labeling（输入和输出一样多）

可以通过串联输入的 vector （让 FC 考虑上下文）

但是有的任务考虑一个 window 不行，而是需要考虑整个 sequence，如果用一个 window 覆盖整个 FC，参数会特别多，并且容易 overfitting。

有没有更好的方法来考虑整个 Input Sequence 的信息？

Self-attention

Self-attention 可以叠加很多次。Self-attention 处理整个 Sequence 的信息，Fully connected Network 专注于处理某一个位置的 信息。

Self-attention 可以将所有数据一起输入，考虑整个 sequence，输入几个 vector，输出就几个 vector（这 几个 vector 是考虑整个 Sequence 得到的）。然后将考虑整个句子的 vector 丢到 Fully connected Network，然后再来决定它应该是什么样的东西。 此时的 FC 是会考虑整个 window 才决定要输出什么样的结果。

Self-attention 如何运作：它的 input 是一串的 vector，每个 $b$ 是考虑了所有的 $a$ 才生成出来的。

如何产生 $b$

如何产生 $b^1$ 这个向量：

1. 根据 $a^1$ 找出这个 Sequence 里面跟 $a^1$ 相关的其它向量，每一个向量跟 $a^1$ 的关联的程度用一个数值 $\alpha$ 表示。

2. Self-attention 如何决定两个向量的关联程度呢？
   将两个 vector 作为输入，输出是两个向量的关联程度

Dot-product

1）Dot-product
将 两个向量乘以不同的矩阵 $W^q$ 和 $W^k$，得到两个 向量 $q$ 和 $k$，然后将 $q$ 和 $k$ 作 Dot-product 以后，得到一个 Scalar $\alpha$
2）Additive

比较常用的方法是 Dot-product

Attention Score

如何将它套用到 Self-attention 中呢？

需要分别计算 向量 两两之间的关联性。
将 $a^1$ 乘 $W^q$ 得到 向量 $q^1$ (query)
将 $a^{\mathrm{2..}n}$ 乘 $W^k$ 得到向量 $k^{\mathrm{2..}n}$，然后分别与 $q^1$ 作 Inner-product，就得到 ${\alpha }_{1,\mathrm{2..}n}$

${\alpha }_{1,2}$ 代表 query 是 $1$ 提供的，key 是 $2$ 提供的时候，$1$ 跟 $2$ 它们之间的关联性（Attention 的 Score）。

一般 $q^1$ 也会和自己 算关联性。
计算出 $a^1$ 和其它向量的关联性之后作 soft-max 得到 ${\alpha }^{\prime }$

接下来我们就要根据这个 ${\alpha }^{\prime }$ 抽取 Sequence 里面重要的资讯。
根据 $\alpha$ 我们已经知道哪些向量跟 $a^1$ 是最有关系的，接下来要根据关联性(Score) 抽取重要的资讯。

抽取重要信息

如何抽取重要的资讯呢？
要 $a^{\mathrm{1..}n}$ 每个向量乘上 $W^v$ 得到新的向量 $v^{\mathrm{1..}n}$，然后将 $v^1$ 到 $v^n$ 每个向量都去乘上 ${\alpha }^{\prime }$，然后再把它加起来得到 $b^1$。

如果 $a^1$ 和 $a^2$ 的关联性比较高 $a_{1,2}^{\prime }$ 比较大的话，得到的 $b^1$ 的值就会比较接近 $v^2$。
所以如何谁的 Attention 的分数越大，谁的 $v$ 就越接近最终抽取出来的结果。

$b^{\mathrm{1..}n}$ 可以同时产生。

从矩阵乘法角度理解如何运作：

每一个 $a$ 都要产生 $q$、$k$、$v$。

所以可以把 $a^{\mathrm{1..}n}$ 拼起来看作是一个矩阵 $I$，然后乘 $W^q$ 矩阵，就得到了 $q^{\mathrm{1..}n}$ 即 $Q$ 矩阵，$k$ 和 $v$ 同理。

每一个 $q$ 都会和每一个 $k$ 作 inner product 得到 attention 的分数，所以可以简化为矩阵相乘。
所以 可以得到 $A^{\prime }$ 矩阵，里面包含任意两个 $a$ 之间的相关性。

现在就可以通过 $A^{\prime }$ 和 $V$ 矩阵相乘得到每一个 $b$，组成矩阵 $O$。

所以整个问题就可以等价于 矩阵相乘。

整个 Self-attention 中只有 $W^q$ $W^k$ $W^v$ 是未知的，是需要学习出来的。

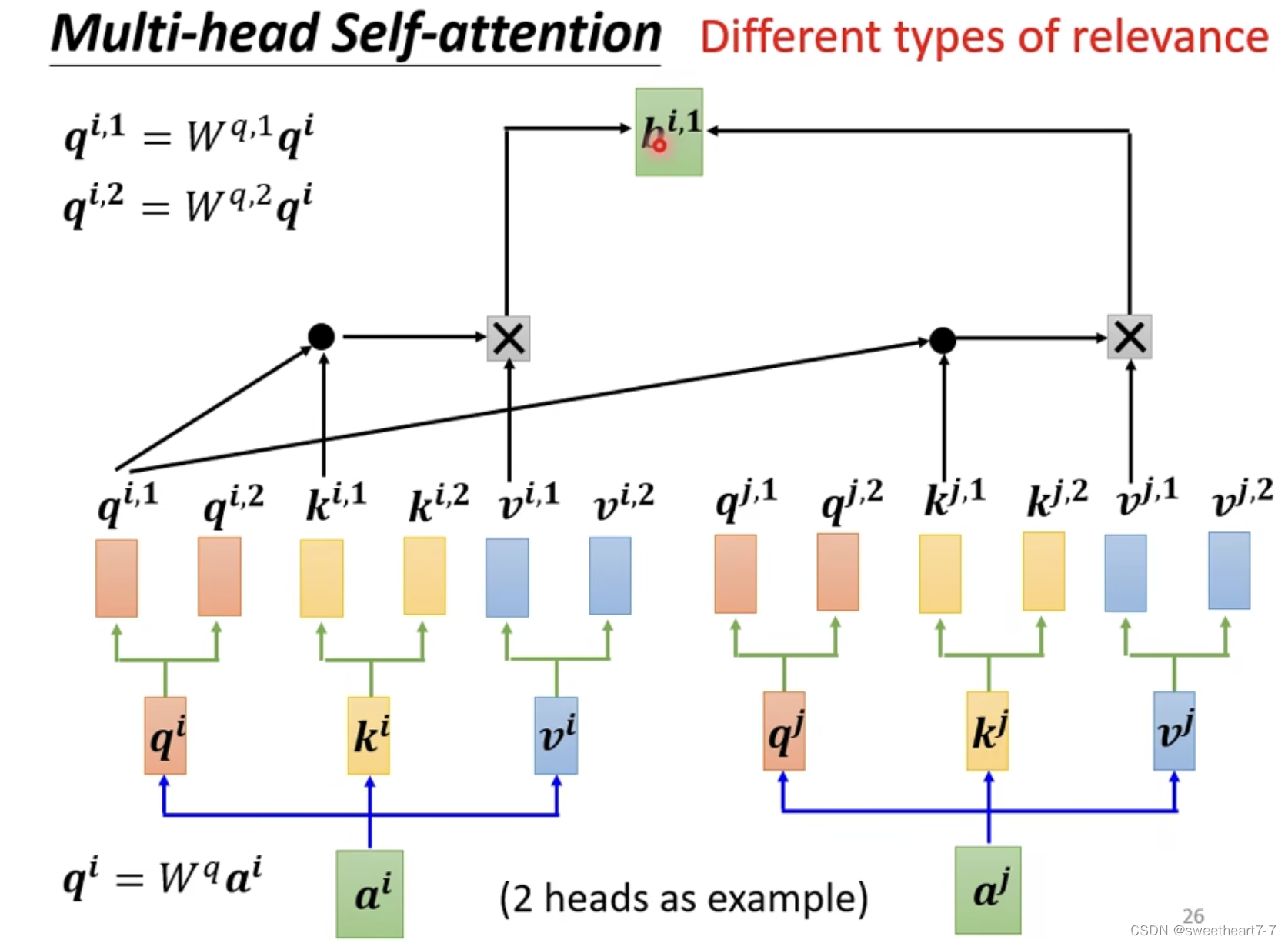
Multi-head Self-attention

Self-attention 进阶版本 Multi-head Self-attention

可能会有多种相关性，所以需要多个 $q$、$k$、$v$

分别对每个 head 作之前的计算就行。

positional encoding

前面的 Self-attention 没有考虑位置信息，但是考虑位置信息可能训练结果会更好。

所以如何将位置资讯加到 Self-attention 呢？

需要用到 positional encoding 的技术。

1. 对每一个位置设定一个 positional vector，用 $e^i$ 来表示，$i$ 代表不同的位置。
2. 将 $e$ 加到 $a$ 上就行了。

Self-attention 的应用：

语音识别也可以用 Self-attention。
但是 Attention Matrix 可能会很大，可以用 Truncated Self-attention 解决（只看一个小范围）。

Self-attention 也可以用到 图像识别上。

Self-attention vs CNN

Self-attention 考虑整张图片，而 CNN 只考虑一个小范围。
CNN 可以看作是一个简化版的 Self-attention。

不同 大小 data 下训练结果的比较

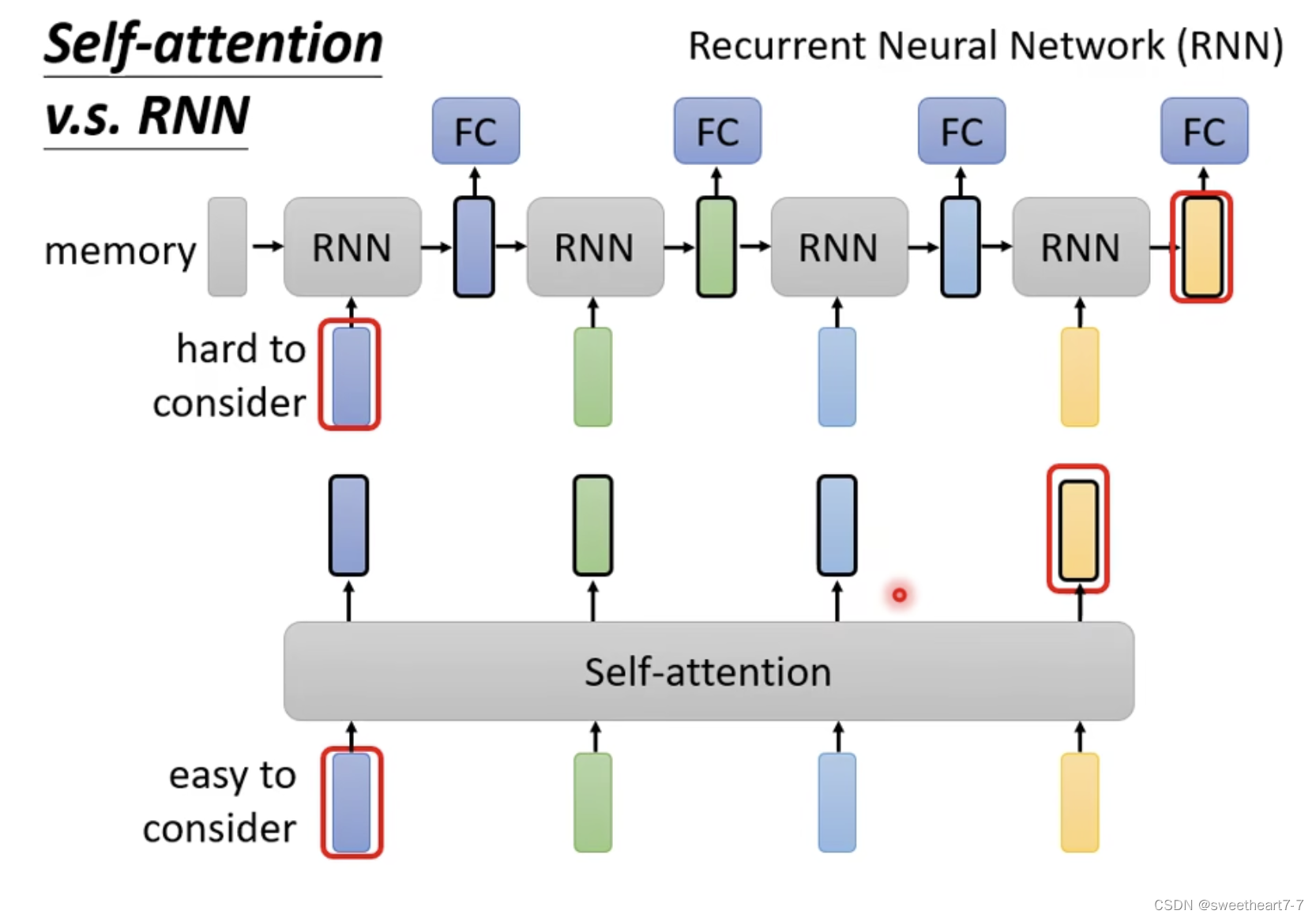
Self-attention vs RNN

RNN 有 Memory，太远的资讯容易忘记，而且不能平行处理。

Self-attention 也可以用到 Graph 上 ⇒ GNN。

Self-attention 的众多变形。