1. 图的定义【含有：阶】

图 G 由顶点集 V 和边集 E 组成，记为 G = (V, E) ，
其中 V(G) 表示图 G 中顶点的有限非空集； E(G) 表示图 G 中顶点之间的关系（边）集合。
若 V={v1,v2,…,vn}，则用 |V| 表示图 G 中顶点的个数，也称 图 G 的阶。
E={(u,v)∣u∈V,v∈V}【即u，v都是顶点】，用 |E| 表示图 G 中边的条数。

注意：线性表可以是空表，树可以是空树，但图不可以是空，即V一定是非空集。

2. 无向图、有向图【含有：边、弧、弧头、弧尾】

3. 简单图、多重图

4. 顶点的度、入度、出度

---

5. 顶点-顶点的关系描述【路径、回路、环、路径长度、简单路径、路径长度、点到点的距离】

路径：顶点 v_p​ 到顶点 v_q​ 之间的一条路径——>是指顶点序列 v_p ，v_i1，v_i2，v_i3，…，v_q​。

回路（或环）：第一个顶点和最后一个顶点相同的路径。

简单路径：在路径序列中，顶点不重复出现的路径称为简单路径。

简单回路： 除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路。

路径长度：路径上边的数目。

点到点的距离：从顶点 u 出发到顶点 v 的最短路径若存在，则此路径的长度称为从 u 到 v 的距离。若从 u 到 v 根本不存在路径，则记该距离为无穷∞。

---

6. 连通图【无向图】、强连通图【有向图】

无向图中：只要两个顶点有一条边，顶点就是连通的
有向图中：只要两个顶点能【A—>B，B—>A】，顶点就是连通的

---

7. 子图、生成子图

设有两个图G = (V, E)和G’ = (V’, E’)：
若V’是V的子集，且E’是 E的子集，则称G’是G的子图。

若有满足V(G’) = V(G)的子图G’，则称其为G的生成子图【即在子图的基础上】

---

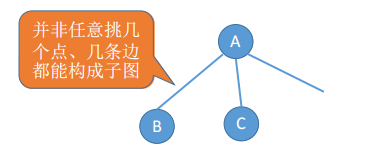
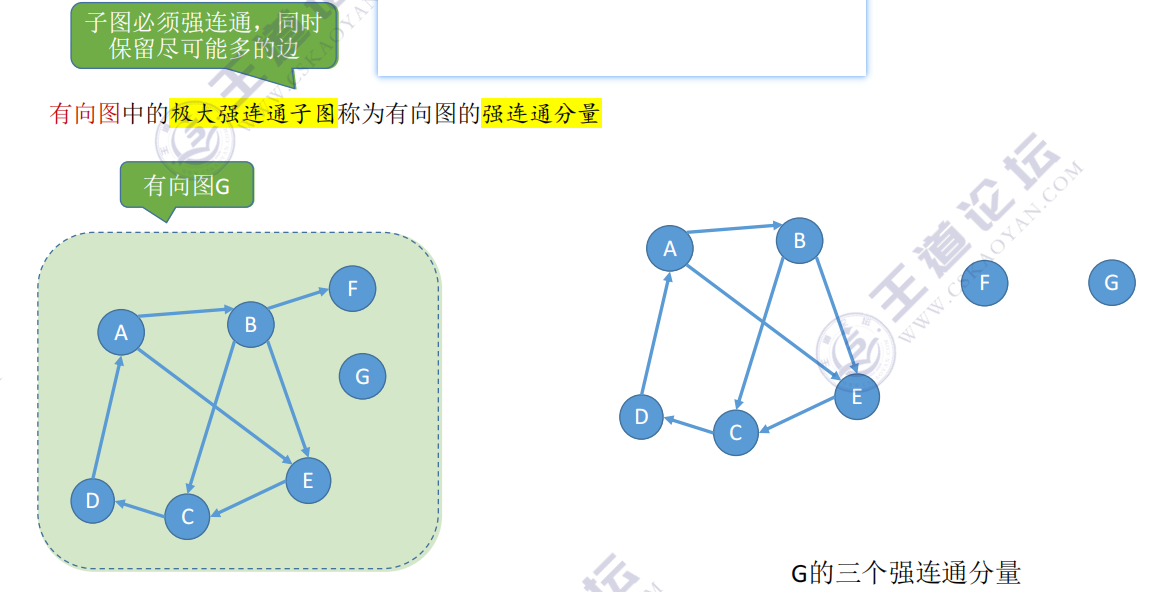
8. 连通分量【含有极大连通子图】、强连通分量【含有极大强连通子图】

无向图：
  
  
有向图：
  

---

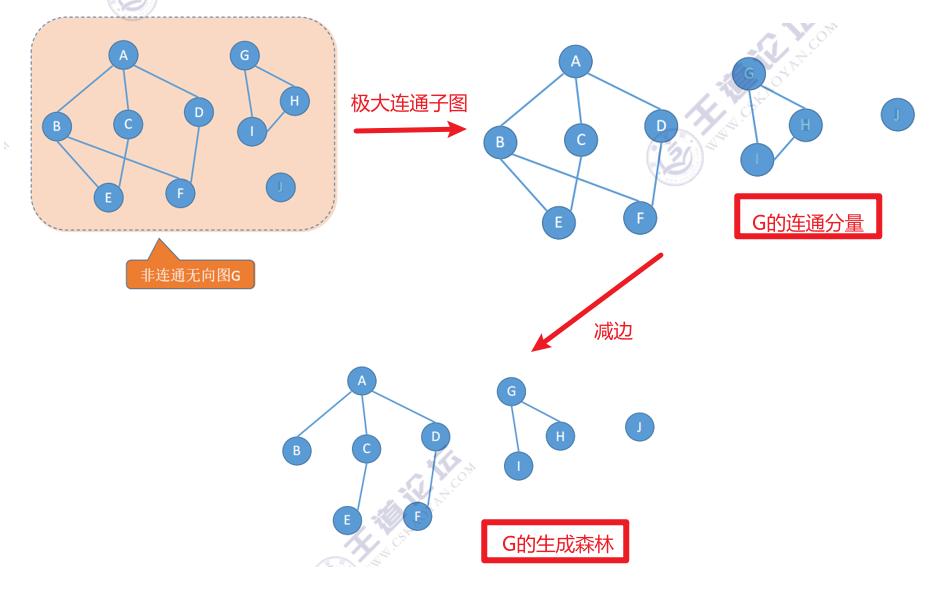
9. 生成树：包含图中全部顶点的一个【极小连通子图】。

---

10. 生成森林 【求G的连通分量，再减边—>G的生成森林】

在非连通图中，连通分量的生成树构成了非连通图的生成森林

11. 边的权、带权图（也称网）、带权路径长度

边的权：在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值。

带权图（也称网）：边上带有权值的图。

带权路径长度：当图是带权图时，一条路径上所有边的权值之和。

12. 无向完全图、有向完全图

13. 稀疏图、稠密图

14. 树、森林、有向树