-
离散数学复习:谓词逻辑
谓词逻辑(一阶逻辑)
1. 谓词的引入
1.1 命题逻辑的局限性

1.2 个体词和谓词


1.2.1 个体词
个体词可以分为两种,个体常量和个体变量,均在个体域内取值。
- 表示具体或特定的个体词称为个体常量。一般用带或不带下标的小写英文字母 a , b , c , . . . , a 1 , b 1 , c 1 , . . . a,b,c,... ,a_1,b_1, c_1,... a,b,c,...,a1,b1,c1,...等表示。
- 表示抽象的或泛指的个体词称为个体变量。一般用带或不带下标的小写英文字母 x , y , z , . . . , x 1 , y 1 , z 1 , . . . x,y,z,... ,x_1,y_1,z_1,... x,y,z,...,x1,y1,z1,... 等表示。
- 个体词的取值范围称为个体域,常用D来表示
- 宇宙间的所有个体域聚集在一起所构成的个体域称为全总个体域。 若无特别说明,均使用全总个体域。
1.2.2 谓词
设D为非空的个体域,定义在 D n D^n Dn(表示n个个体都在个体域D上取值)上取值于{0,1} 上的n元函数,称为n元命题函数或n元谓词,记为 P ( x 1 , x 2 , . . . , x n ) P(x_1,x_2,... ,x_n) P(x1,x2,...,xn)。其中,个体变量 x 1 , x 2 , . . . , x n ∈ D x_1,x_2,... ,x_n∈D x1,x2,...,xn∈D。
- 表示具体性质或关系的谓词称为谓词常量。
- 表示抽象的或泛指的性质或关系的谓词称为谓词变量。
谓词均使用大写英文字母 P , Q , R , . . , F , G , H , . . . P, Q,R,..,F,G, H,... P,Q,R,..,F,G,H,...来表示。

1.2.3 复合谓词的命题符号化情况

1.3 总结

2. 量词的引入
虽然有了个体词和谓词,但是对于有些命题而言,还是无法准确描述:

2.1 量词
- 全称量词: ∀ \forall ∀,所有的x,任意的x,一切的x,每一个x
- 存在量词: ∃ \exists ∃,有些,至少有一个x,某一些x,存在x
其中的x称为作用变量。一般将其量词加在其谓词之前,记为 ( ∀ x ) F ( x ) , ( ∃ x ) F ( x ) (\forall x)F(x) , (\exist x)F(x) (∀x)F(x),(∃x)F(x)。此时, F(x)称为全称量词和存在量词的辖域。

2.2 个体域符号化
使用全总个体域:

统一个体域为全总个体域,而对每一个句子中个体变量的变化范围用一 元特性谓词刻划之。这种特性谓词在加入到命题函数中时必定遵循如下原则:
- 对于全称量词 ∀ ( x ) \forall(x) ∀(x) ,刻划其对应个体域的特性谓词作为蕴涵式之前件加入。
- 对于存在量词 ∃ ( x ) \exists (x) ∃(x) ,刻划其对应个体域的特性谓词作为合取式之合取项加入。
2.3 量词的真值确定

量词的顺序不能随便变化:

个体与有限的情况下:

2.4 谓词符号化示例
2.4.1 示例1:一元谓词

2.4.2 示例2:二元谓词

量词对变元的约束往往与量词的次序有关。不同的量词次序,可以产生不同的真值。因此当多个量词同时出现时,不能随意颠倒它们的顺序,否则会改变原有的含义。
2.4.3 示例3:个体域默认选择

3. 谓词合式公式
3.1 四类公式
在基于谓词的形式化中,我们将使用如下四种符号:
- 常量符号:指所属个体域D中的某个元素,用带或不带下标的小写英文字母$a,b,c,… ,a_1,b_1,c_1,… $来表示。
- 变量符号:指所属个体域D中的任意元素,用带或不带下标的小写英文字母 x , y , z , . . . , x 1 , y 1 , z 1 , . . . x,y,z,... ,x_1,y_1,z_1,... x,y,z,...,x1,y1,z1,...来表示。
- 函数符号:n元函数符号 f ( x 1 , x 2 , . . . , x n ) f(x_1, x_2,... ,x_n) f(x1,x2,...,xn)可以是所属个体域集合 D n → D D^n→D Dn→D的任意一个函数,用带或不带下标的小写英文字母 f , g , h , . . . , f 1 , g 1 , h 1 , . . . f,g,h,... ,f_1,g_1,h_1,... f,g,h,...,f1,g1,h1,...来表示。【函数符号的最终取值是个体域中的个体】
- 谓词符号:n元谓词符号 P ( x 1 , x 2 , . . . , x n ) P(x_1, x_2,... ,x_n) P(x1,x2,...,xn)可以是所属个体域集合 D n → { 0 , 1 } D^n→\{0, 1\} Dn→{0,1}的任意一个谓词,用带或不带下标的大写英文字母 P , Q , R , . . . , P 1 , Q 1 , R i , . . . P, Q,R,... ,P_1,Q_1, R_i,... P,Q,R,...,P1,Q1,Ri,...来表示。【谓词符号的最终取值是0或者1】
3.2 项
谓词逻辑中的项( Term),被递归地定义为:
- 任意的常量符号或任意的变量符号是项;
- 若 f ( x 1 , x 2 , . . . , x n ) f(x_1,x_2,... ,x_n) f(x1,x2,...,xn)是n元函数符号, t 1 , t 2 , . . . , t n t_1,t_2,... ,t_n t1,t2,...,tn是项,则 f ( t 1 , t 2 , . . . , t n ) f(t_1,t_2,... ,t_n) f(t1,t2,...,tn)是项
仅由有限次使用以上两个规则产生的符号串才是项。

3.3 谓词公式
Definition:若 P ( x 1 , x 2 , . . . , x n ) P(x_1,x_2, ... ,x_n) P(x1,x2,...,xn)是n元谓词, t 1 , t 2 , . . . , t n t_1,t_2,... ,t_n t1,t2,...,tn 是项,则称 P ( t 1 , t 2 , . . . , t n ) P(t_1, t_2,... ,t_n) P(t1,t2,...,tn)为原子谓词公式,简称原子公式。


3.4 自由变元和约束变元
3.4.1 定义
给定一个合式公式G,若变元x出现在*使用变元的量词的辖域之内*,则称变元x的出现为约束出现,此时的变元x称为约束变元。若x的出现不是约束出现,则称它为自由出现,此时的变元x称为自由变元。

3.4.2 两个规则

规则1:约束规则的改名规则
- 将量词中的变元以及该量词辖域中此变量之所有约束出现都用新的个体变元替换;
- 新的变元-定要有别于改名辖域中的所有其它变量。
规则2:自由变元的代入规则
- 将公式中出现该自由变元的每一处都用新的个体变元替换 ;
- 新的变元不允许在原公式中以任何约束形式出现。也可用个体常量代入。
3.5 闭式

4. 公式的解释与分类
4.1 公式的解释

公式解释的概念:

4.2 公式的分类
- 如果公式G在它所有的解释下都取值为真,则称G为有效公式。
- 如果公式G在它所有的解释下都取值为假,则称G为矛盾公式。
- 如果至少有一个解释下取值为真,则称G为可满足公式。

5. 公式的等价关系
5.1 等价关系的定义
定义:如果 G ↔ H G\leftrightarrow H G↔H是有效公式,则公式G,H是等价的,记为 G = H G=H G=H
定义:设 G ( P 1 , P 2 , . . . , P n ) G(P_1,P_2,...,P_n) G(P1,P2,...,Pn)是命题演算中的命题公式, P 1 , P 2 , . . . , P n P_1,P_2,...,P_n P1,P2,...,Pn是出现在命题G中的命题变元,当用任意的谓词公式 G i ( 1 ≤ i ≤ n ) G_i(1\leq i\leq n) Gi(1≤i≤n)分别代入 P i P_i Pi后,得到新的谓词公式 G ( G 1 , G 2 , . . . , G n ) G(G_1,G_2,...,G_n) G(G1,G2,...,Gn)称为原公式的代入实例。
- 永真公式的一个代入实例必然是有效公式
- 基本等价公式在谓词逻辑找那个仍然成立
5.2 基本等价关系
定理:
假设 G ( x ) , H ( x ) G(x),H(x) G(x),H(x)是只含有自由变元 x x x的公式,S是不含有 x x x的公式,则在全总个体域中,有:
E 25 : ( ∃ x ) G ( x ) = ( ∃ y ) G ( y ) ; E_{25}: (\exists x)G(x)=(\exists y)G(y); E25:(∃x)G(x)=(∃y)G(y);
E 26 : ( ∀ x ) G ( x ) = ( ∀ y ) G ( y ) ; E_{26}:(\forall x)G(x)=(\forall y)G(y); E26:(∀x)G(x)=(∀y)G(y); 改名规则
E 27 : ¬ ( ∃ x ) G ( x ) = ( ∀ x ) ¬ G ( x ) ; E_{27}:\neg (\exists x)G(x)=(\forall x)\neg G(x); E27:¬(∃x)G(x)=(∀x)¬G(x);
E 28 : ¬ ( ∀ x ) G ( x ) = ( ∃ x ) ¬ G ( x ) E_{28}:\neg (\forall x)G(x)=(\exists x)\neg G(x) E28:¬(∀x)G(x)=(∃x)¬G(x) 量词转换律/量词否定等价式

E 29 : ( ∀ x ) ( G ( x ) ∨ S ) = ( ∀ x ) G ( x ) ∨ S E_{29}:(\forall x)(G(x) \vee S)=(\forall x) G(x) \vee S E29:(∀x)(G(x)∨S)=(∀x)G(x)∨S;
E 30 : ( ∀ x ) ( G ( x ) ∧ S ) = ( ∀ x ) G ( x ) ∧ S E_{30}:(\forall x)(G(x) \wedge S)=(\forall x) G(x) \wedge S E30:(∀x)(G(x)∧S)=(∀x)G(x)∧S.
E 31 : ( ∃ x ) ( G ( x ) ∨ S ) = ( ∃ x ) G ( x ) ∨ S E_{31}:(\exists x)(G(x) \vee S)=(\exists x) G(x) \vee S E31:(∃x)(G(x)∨S)=(∃x)G(x)∨S.
E 32 : ( ∃ x ) ( G ( x ) ∧ S ) = ( ∃ x ) G ( x ) ∧ S E_{32}:(\exists x)(G(x) \wedge S)=(\exists x) G(x) \wedge S E32:(∃x)(G(x)∧S)=(∃x)G(x)∧S. 量词辖域的收缩与扩张
E 33 : ( ∀ x ) ( G ( x ) ∧ H ( x ) ) = ( ∀ x ) G ( x ) ∧ ( ∀ x ) H ( x ) E_{33}:(\forall x)(G(x) \wedge H(x))=(\forall x) G(x) \wedge(\forall x) H(x) E33:(∀x)(G(x)∧H(x))=(∀x)G(x)∧(∀x)H(x);
E 34 : ( ∃ x ) ( G ( x ) ∨ H ( x ) ) = ( ∃ x ) G ( x ) ∨ ( ∃ x ) H ( x ) E_{34}:(\exists x)(G(x) \vee H(x))=(\exists x) G(x) \vee(\exists x) H(x) E34:(∃x)(G(x)∨H(x))=(∃x)G(x)∨(∃x)H(x). 量词分配律

5.3 范式
在命题逻辑里,每一公式都有与之等值的范式,范式是一种统一的表达形式,当研究一个公式的特点(如永真、永假)时,范式起着重要作用。对谓词逻辑的公式来说,也有范式,其中前束范式与原公式是等值的,而其它范式与原公式只有较弱的关系。
5.3.1 定义

5.3.2 求解步骤


6. 谓词综合推理
6.1 推理形式和推理规则
6.1.1 推理形式
定义:设 G 1 , G 2 , . . . , G n , H G_1,G_2,... ,G_n, H G1,G2,...,Gn,H是公式,称 H H H是 G 1 , G 2 , . . . , G n G_1, G_2,... , G_n G1,G2,...,Gn的逻辑结果(或称 G 1 , G 2 , . . , G n G_1, G_2,..,G_n G1,G2,..,Gn共同蕴涵H)当且仅当对任意解释 I I I,若 I I I同时满足 G 1 , G 2 , . . . , G n G_1,G_2,... ,G_n G1,G2,...,Gn,则满足H,记为 G 1 , G 2 , . . . , G n → H G_1,G_2,... ,G_n→H G1,G2,...,Gn→H,此时称 G 1 , G 2 , . . . , G n ⇒ H G_1,G_2,... ,G_n\Rightarrow H G1,G2,...,Gn⇒H是有效的,否则称为无效的。 G 1 , G 2 , . . . , G n G_1, G_2,... ,G_n G1,G2,...,Gn称为一组前提(premise) ,有时用集合F来表示,记 Γ = { G 1 , G 2 , . . . , G n } \Gamma= \{G1,G2,... ,Gn\} Γ={G1,G2,...,Gn}, H H H称为结论(conclusion) ,又称H是前提集合 Γ \Gamma Γ的逻辑结果,记为 Γ → H \Gamma→H Γ→H。

6.1.2 推理规律

6.1.3 推理规则
消去和引入量词的4种规则
6.1.3.1 全称特指规则US

6.1.3.2 存在特指规则ES

6.1.3.3 全称推广规则UG

6.1.3.4 存在推广规则EG

6.2 综合推理方法
6.2.1 基本方法


6.2.2 难点总结
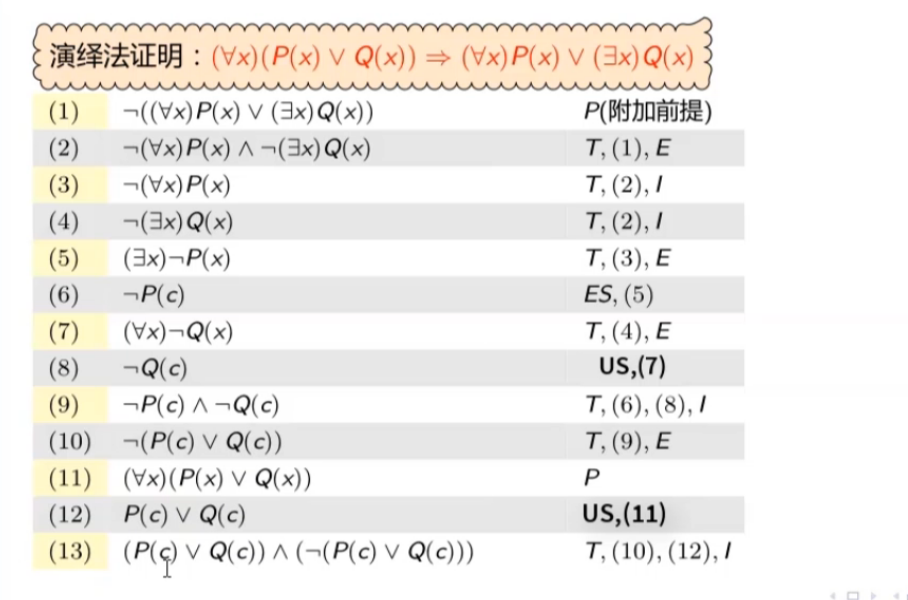
在推导过程中,如既要使用规则US又要使用规则ES消去量词,而且选用的个体是同一个符号,则必须先使用规则ES,再使用规则US。然后再使用命题演算中的推理规则,最后使用规则UG或规则EG引入量词,得到所求结论。
- 如一个变量是用规则ES消去量词,对该变量在添加量词时,则只能使用规则EG ;
- 如使用规则US消去量词,对该变量在添加量词时,则可使用规则EG和规则UG。
- 在用规则US和规则ES消去量词时,此量词必须位于整个公式的最前端,且辖域为其后的整个公式。
- 在添加量词 ∀ x \forall x ∀x和 ∃ x \exists x ∃x时,所选用的 x x x不能在公式 G ( y ) G(y) G(y)或 G ( c ) G(c) G(c)中出现。
-
相关阅读:
Hudi DeltaStreamer使用总结
C#实现OPC DA转OPC UA服务器
冥想第六百一十天
C++:stl:list的常用接口及其模拟实现
java计算机毕业设计阳明湖风景区订票系统源程序+mysql+系统+lw文档+远程调试
硫化锌量子点/ZnS QDs 巯基SH/氨基/NH2/羧基COOH修饰硫化锌量子点/ZnS QDs
一文了解 Go 接口
微信小程序(基础语法)
力扣106 补9.11
什么是数据库迁移
- 原文地址:https://blog.csdn.net/weixin_45745854/article/details/126334225