• 【考研】数据结构考点——堆排序（含408真题）

    ​前言

    本文内容源于对《数据结构（C语言版）》（第2版）、王道讲解学习所得心得、笔记整理和总结。

    选择排序的基本思想：每一趟从待排序的记录中选出关键字最小的记录，按顺序存放在已排序的记录序列的最后，直到全部排完为止。

    选择排序的主要两种方法：直接选择排序、堆排序。

    本文内容主要针对堆排序。

    在本文最后的练习的中，以举例子说明该排序方法，配以图文，讲解详细（含408真题）。

    本文“干货”较足，建议收藏。

    可搭配以下链接一起学习：

    【考研复习：数据结构】查找（不含代码篇）_住在阳光的心里的博客-CSDN博客

    【考研】《数据结构》知识点总结.pdf_考研数据结构知识点总结背诵-其它文档类资源-CSDN文库

    【考研】数据结构考点——直接选择排序_住在阳光的心里的博客-CSDN博客

    目录

     前言

            一、基本概念

                    1、堆排序 (Heap Sort) 的定义

            ​​​​​​​        2、堆的定义

            ​​​​​​​        3、堆排序步骤（大根堆）

            二、调整堆

            ​​​​​​​        （一）举例说明

            ​​​​​​​        （二）算法步骤

            ​​​​​​​        （三）算法描述

            三、建初堆

            ​​​​​​​        （一）举例说明

            ​​​​​​​        （二）算法步骤

            ​​​​​​​        （三）算法描述

            四、堆排序算法的实现

            ​​​​​​​        （一）算法代码

            ​​​​​​​        （二）举例说明

            ​​​​​​​        （三）算法分析

            ​​​​​​​        （四）算法特点

            五、练习

    一、基本概念

    1、堆排序 (Heap Sort) 的定义

    是一种树形选择排序。

    在排序过程中，将待排序的记录 r[1...n] 看成是一棵完全二叉树的顺序存储结构，利用完全二叉树中双亲结点和孩子结点之间的内在关系，在当前无序的序列中选择关键字最大(或最小)的记录。

    2、堆的定义

    n 个元素的序列 { k_1,k_2,...,k_n​ } 称之为堆，当且仅当满足以下条件时：

    （1）k_i\geq k_{2i}​ 且 k_i \geq k_{2i+1}​

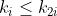    或（2）k_i \leq k_{2i}​ 且 k_i \leq k_{2i+1}​

    若将和此序列对应的一维数组（即以一维数组做此序列的存储结构）看成是一个完全二又树，则堆实质上是满足如下性质的完全二叉树：

    树中所有非终端结点的值均不大于(或不小于)其左、右孩子结点的值。

    3、堆排序步骤（大根堆）

    例如，关键字序列 { 96, 83, 27, 38, 11, 09 } 和 { 12, 36, 24, 85, 47, 30, 53, 91} 分别满足条件 (1) 和条件 (2)，故它们均为堆，对应的完全二叉树分别如图 8.9 (a) 和 (b) 所示。

    显然，在这两种堆中，堆顶元素（或完全二叉树的根)必为序列中n个元素的最大值（或最小值），分别称之为大根堆（或小根堆）。

    ​

     堆排序步骤（大根堆）如下：

    1、按堆的定义将待排序序列 r[1..n] 调整为大根堆(这个过程称为建初堆)，交换 r[1] 和 r[n]，则 r[n]为关键字最大的记录。

    2、将 r[1..n-1] 重新调整为堆，交换 r[1] 和 r[n-1] ，则 r[n-1] 为关键字次大的记录。

    3、循环 n - 1 次，直到交换了 r[1] 和 r[2] 为止，得到了一个非递减的有序序列r[1..n]。

    同样，可以通过构造小根堆得到一个非递增的有序序列。

    由此，实现堆排序，需要解决两个问题：一是调整堆，二是建初堆。
     

    二、调整堆

    （一）举例说明

    图8.10(a)是个堆，为大根堆。

    将堆顶元索 97 和堆中最后一个元素 38 交换后，如 8.10(b) 所示，接下来要进行的操作是要将图（b）调整为大根堆。

    由于此时除根结点外，其余结点均满足堆的性质，由此仅需自上至下进行一条路径上的结点调整即可。

    首先以堆顶元素 38 和其左，右子树根结点的值进行比较，由于左子树根结点的值大于右子树根结点的值且大于根结点的值，则将 38 和 76 交换；

    由于 38 替代了 76 之后破坏了左子树的“ 堆 ”， 则需进行和上述相同的调整，直至叶子结点，调整后的状态如图 8.10(c) 所示。

    重复上述过程，将堆顶元素 76 和堆中最后一个元素 27 交换且调整，得到如图 8.(d) 所示新的堆。
    ​

    上述过程像过筛子一样。把较小的关键字逐层筛下去，而将较大的关键字逐层选上来。因此，称此方法为“ 筛选法 ”。

    （二）算法步骤

    假设 r[s+1..m] 已经是堆的情况下，按“ 筛选法 ”将 r[s..m] 调整为以 r[s] 为根的堆，算法实现如下：

    从 r[2s] 和 r[2s+1] 中选出关键字较大者，假设 r[2s] 的关键字较大，比较 r[s] 和 r[2s] 的关键字。

    1、若 r[s].key >= r[2s].key，说明以 r[s] 为根的子树已经是堆，不必做任何调整。

    2、若 r[s].key < r[2s].key，交换 r[s] 和 r[2s]。 交换后，以 r[2s+1] 为根的子树仍是堆，如果以 r[2s] 为根的子树不是堆，则重复上述过程，将以 r[2s] 为根的子树调整为堆，直至进行到叶子结点为止。

    （三）算法描述

    1. //假设r[s+1..m]已经是堆，将r[s..m]调整为以 r[s] 为根的大根堆
    2. void HeapAdjust (SqList &L, int s, int m){
    3.     rc = L.r[s] ;
    4.     for(j = 2*s; j <= m; j *= 2)     //沿 key 较大的孩子结点向下筛选
    5.  
    6.         if (j < m && L.r[j].key < L.r[j+1].key) 
    7.             ++j;      // j 为 key 较大的记录的下标
    8.  
    9.         if(rc.key >= L.r[j].key) 
    10.             break;     //rc应插入在位置s上
    11.  
    12.         L.r[s] = L.r[j];
    13.         s = j;
    14.     }
    15.  
    16.     L.r[s] = rc;     //插入
    17. }

    三、建初堆

    要将一个无序序列调整为堆，就必须将其所对应的完全叉树中以每 结点为根的子树都调整为堆。显然，只有一个结点的树必是堆，而在完全二叉树中，所有序号大于 \left \lfloor \frac{n}{2} \right \rfloor​ 的结点都是叶子，因此以这些结点为根的子树均已是堆。这样，只需利用筛选法，从最后一个分支结点 \left \lfloor \frac{n}{2} \right \rfloor​ 开始，依次将序号为 \left \lfloor \frac{n}{2} \right \rfloor​、\left \lfloor \frac{n}{2} \right \rfloor-1​ 、...、1 的结点作为根的子树都调整为堆即可。 

    （一）举例说明

    已知无序序列为{49, 38, 65, 97, 76, 13, 27, 49}，用 "筛选法” 将其调整为个大根堆，给出建堆的过程。

    从图 8.11 (a) 所示的无序序列的最后一个非终端绪点开始筛选，

    即从第 4 个元素 97 开始，由于 97 > 49，则无需交换。

    同理，第 3 个元素 65 不小于其左、右子树根的值，仍无需交换。

    而第 2 个元素 38 < 97，被筛选之后序列的状态如图 8.11 (b) 所示，然后对根元素 49 筛选之后得到图 8.11 (c) 所示的大根堆。
     

    ​


    （二）算法步骤

    1、对于无序序列 r[1..n] 从 i = n/2 开始，反复调用筛选法 HeapAdjust (L, i, n)。

    2、依次将以 r[i], r[i-1]，...，r[1] 为根的子树调整为堆。

    （三）算法描述

    1. /*
    2. //假设r[s+1..m]已经是堆，将r[s..m]调整为以 r[s] 为根的大根堆
    3. void HeapAdjust (SqList &L, int s, int m){
    4.     rc = L.r[s] ;
    5.     for(j = 2*s; j <= m; j *= 2)     //沿 key 较大的孩子结点向下筛选
    7.         if (j < m && L.r[j].key < L.r[j+1].key) 
    8.             ++j;      // j 为 key 较大的记录的下标
    10.         if(rc.key >= L.r[j].key) 
    11.             break;     //rc应插入在位置s上
    13.         L.r[s] = L.r[j];
    14.         s = j;
    15.     }
    17.     L.r[s] = rc;     //插入
    18. }
    20. */
    21.  
    22. //把无序序列 L.r[1..n] 建成大根堆
    23. void CreatHeap (SqList &L){
    24.     n = L.length;
    25.     for(i = n/2; i > 0; --i)     //反复调用HeapAdjust
    26.         HeapAdjust (L, i, n);
    27. }

    四、堆排序算法的实现

    （一）算法代码

    根据前面堆排序算法步骤的描述，可知堆排序就是将无序序列建成初堆以后，反复进行交换和堆调整。在建初堆和调整堆算法实现的基础上，下面给出堆排序算法的实现。

    1. //对顺序表L进行堆排序
    2. void HeapSort (SqList &L){
    3.     CreatHeap(L);     //把无序序列 L.r[1..L.length] 建成大根堆
    4.     for(i = L.length; i > 1; --i){
    5.         x = L.r[1]:     //将堆顶记录和当前未经排序子序列 L.r[1..i] 中最后一个记录互换
    6.         L.r[1] = L.r[i];
    7.         L.r[i] = x; 
    8.         HeapAdjust(L, 1, i-1);      //将 L.r[1..i-1] 重新调整为大根堆
    9.     }
    10. }
    11.  
    12. /*
    13. //假设r[s+1..m]已经是堆，将r[s..m]调整为以 r[s] 为根的大根堆
    14. void HeapAdjust (SqList &L, int s, int m){
    15.     rc = L.r[s] ;
    16.     for(j = 2*s; j <= m; j *= 2)     //沿 key 较大的孩子结点向下筛选
    18.         if (j < m && L.r[j].key < L.r[j+1].key) 
    19.             ++j;      // j 为 key 较大的记录的下标
    21.         if(rc.key >= L.r[j].key) 
    22.             break;     //rc应插入在位置s上
    24.         L.r[s] = L.r[j];
    25.         s = j;
    26.     }
    28.     L.r[s] = rc;     //插入
    29. }
    32. //把无序序列 L.r[1..n] 建成大根堆
    33. void CreatHeap (SqList &L){
    34.     n = L.length;
    35.     for(i = n/2; i > 0; --i)     //反复调用HeapAdjust
    36.         HeapAdjust (L, i, n);
    37. }
    39. */

    （二）举例说明

    已知待排序记录的关键字序列为 {49, 38, 65, 97, 76, 13, 27, 49}，给出用堆排序法进行排序的过程。

    解：首先将无序序列建初堆，过程如图 8.11所示。（在 “三、建初堆” 的 “（一）举例说明” 处）

    在初始大根堆的基础上，反复交换堆顶元素和最后一个元素，然后重新调整堆，直至最后得到一个有序序列，整个堆排序过程如下图所示。

    ​

    ​

    （三）算法分析

    1、时间复杂度

    堆排序的运行时间主要耗费在建初堆和调整堆时进行的反复“筛选”上。

    设有 n 个记录的初始序列所对应的完全二叉树的深度为 h，建初堆时，每个非终端结点都要自上而下进行“筛选”。

    由于第 i 层上的结点数小于等于 2^{i-1}​ ，且第 i 层结点最大下移的深度为 h - i ，每下移一层要做两次比较，所以建初堆时关键字总的比较次数为

    ​

    所以，在建含 n 个元素的堆时，关键字的比较总次数不超过 4n。

    调整建新堆时要做 n - 1 次“筛选”， 每次“筛选"都要将根结点下移到合适的位置。n个结点的完全二叉树的深度为 \left \lfloor log_2n \right \rfloor+1​，则重建堆时关键字总的比较次数不超过

    ​

     由此，堆排序在最坏的情况下，其时间复杂度也为 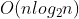O(nlog_2n)​。实验研究表明，平均性能接近于最坏性能。

    2、空间复杂度

    仅需一个记录大小供交换用的辅助存储空间，所以空间复杂度为 O(1)。
     

    （四）算法特点

    1、是不稳定排序。

    2、只能用于顺序结构，不能用于链式结构。

    3、初始建堆所需的比较次数较多，因此记录数较少时不宜采用。堆排序在最坏情况下时间复杂
    度为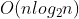 O(nlog_2n)​，相对于快速排序最坏情况下的 O(n^2)​ 而言是一个优点， 当记录较多时较为高效。

    五、练习

    1、数据表中有10000个元素，如果仅要求求出其中最大的10个元素，则采用（     D     ）算法最节省时间。

    A. 希尔排序                    B. 快速排序                   C. 冒泡排序                    D. 堆排序

    2、下列关键字序列中，（      D     ）是堆。

    A. 16，72，31，23，94，53                                        B. 94，23，31，72，16，53

    C. 16，53，23，94，31，72                                        D. 16，23，53，31，94，72

    解：如下图：

    ​

    ​

    3、有组记录的排序码为（46，79，56，38，40，84），则利用堆排序的方法建立的初始堆为（     B    ）

    A. 79，46，56，38，40，84                                        B. 84，79，56，38，40，46

    C.  84，79，56，46，40，38                                       D. 84，56，79，40，46，38

    解：建初堆， 利用筛选法，从最后一个分支结点 \left \lfloor \frac{n}{2} \right \rfloor​ 开始，依次将序号为 \left \lfloor \frac{n}{2} \right \rfloor​、\left \lfloor \frac{n}{2} \right \rfloor-1​ 、...、1 的结点作为根的子树都调整为堆即可。 则如下图：

    ​

     4、已知关键字序列 5, 8, 12, 19, 28, 20, 15, 22 是小根堆，插入关键字3，调整后得到的小根堆是(     A      )

    A. 3，5，12，8，28，20，15，22，19

    B. 3，5，12，19，20，15，22，8，28

    C. 3，8，12，5，20，15，22，28，19

    D. 3，12，5，8，28，20，15，22，19

    解：如下图：

    ​

    ​

    5、下列关于大根堆（至少含 2个元素）的叙述中，正确的是（    C    ）

    Ⅰ. 可以将堆看成一棵完全二叉树
    Ⅱ. 可以采用顺序存储方式保存堆
    Ⅲ. 可以将堆看成一棵二叉排序树
    Ⅳ. 堆中的次大值一定在根的下一层
    A. 仅Ⅰ、Ⅱ                  B. 仅Ⅱ、Ⅲ                C. 仅Ⅰ、Ⅱ和Ⅳ                 D.Ⅰ、Ⅲ和Ⅳ 

    解：针对 Ⅲ，大根堆只要求根结点值大于左右孩子值，并不要求左右孩子值有序。其余选项可在本文找到答案。

    6、已知小根堆为 8，15，10，21，34，16，12，删除关键字8之后需重建堆，在此过程中，关键字之间的比较次数是（     C     ）

    A. 1                             B. 2                           C. 3                             D. 4 

    解： 删除8后，将12移动到堆顶，第一次是15和10比较，第二次是10和12比较并交换，第三次还需比较12和16，故比较次数为3。如下图所示。

    ​

  • 相关阅读:
    java开发工具IntelliJ IDEA全新版本V2022.2更新详情（一）
    赣菜出赣，2023中国江西国际餐饮产业博览会，餐饮新零售展
    KT142C-sop16语音芯片ic的功能介绍 支持pwm和dac输出 usb直接更新内置空间
    图像识别技术在工业自动化领域的应用与实现
    定位到叠放次序以及定位的拓展
    设计模式-单例模式
    【ftp篇】 vsftp(ftp) 每天生成一个动态密码
    【数据增强】图像数据的几种增广方式
    高项 08 人力资源管理
    19-Redis及Redis集群的介绍、缓存击穿、缓存雪崩、缓存穿透及相应的解决方案
  • 原文地址：https://blog.csdn.net/qq_34438969/article/details/126321448