目录

背包问题的背景是什么？

01背包问题的背景

01背包的分析过程

朴素算法

什么是dp问题的优化？

01背包问题的优化(滚动数组)

---

本文为软件部2022届讲课底稿，作者5月份的时候决定出国，遂卷绩点和英语去了，本文诸多疏漏请多包涵，毕竟不是专业算法选手。

背包问题的背景是什么？

现在有一个背包，体积是v，给定一些物品，这些物品有他们各自的体积vi，也有他们各自的价值权重wi，想要找出怎么装背包，才可以使背包里物品的总价值最大。

问题一：背包必须装满吗？

答：不是。

01背包问题的背景

现在手上有一个背包，给定 n 种物品。物品 i 的重量是 wi，其价值为 vi，背包的容量为 C。问应如 何装入背包中的物品，使得装入背包中物品的总价值最大？ 

问题二：01背包问题物品的选取有什么要求吗？

答：每一种物品只可以选取一次，也可以不选。

01背包的分析过程

问题三：dp问题中要思考的是哪两大方面？

答：

方面一：状态表示表示的是哪个方面的集合？ 01背包问题的集合就是满足条件的所有选法的一种集合。

方面二：状态表示的是哪个方面的属性？最大值？最小值？还是方案总数？

问题四：dp中状态计算的本质是什么？

答：集合的划分

y氏dp分析法（状态机法）：

问题五：状态计算里面选取第i件物品是怎么进行计算的？

答： 这里集合的表示是所有的选法，这里所有的选法都要选取第i件物品，那么第i件物品就不会影响最后的相对结果（好比全班50个同学，小明是第一，所有同学的分数减去100分，小明还是第一，还是那个最优解）。

朴素算法

#include
using namespace std;
const int N=1005;
int dp[N][N];
int v[N],w[N];
int n,m;
 
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>v[i]>>w[i];
	}
	
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			dp[i][j]=max(dp[i][j],dp[i-1][j]);
			if(j>=v[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
		}
	}
	
	cout<
	return 0;
}

什么是dp问题的优化？

在原有的动态规划的式子上，对dp问题的代码或者方程进行等价的变形。 

01背包问题的优化(滚动数组)

问题六：滚动数组是如何进行优化的？

答：二维变一维，减少空间的复杂度。

问题七：滚动数组为什么可以进行优化？

原来的状态方程：dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);dp[i][j] = max(dp[i][j], 答：dp[i - 1][j - v[i]] + w[i]);不难看出，dp[i][j]的下标j是由“j”和“j-v[i]”推导过来的。对于下标i来讲，dp[i][j]只和dp[i][j]以及上一层的dp[i-1][j-v[i]]有关。所以可以用滚动数组。

问题八：滚动数组为什么逆序？

答：

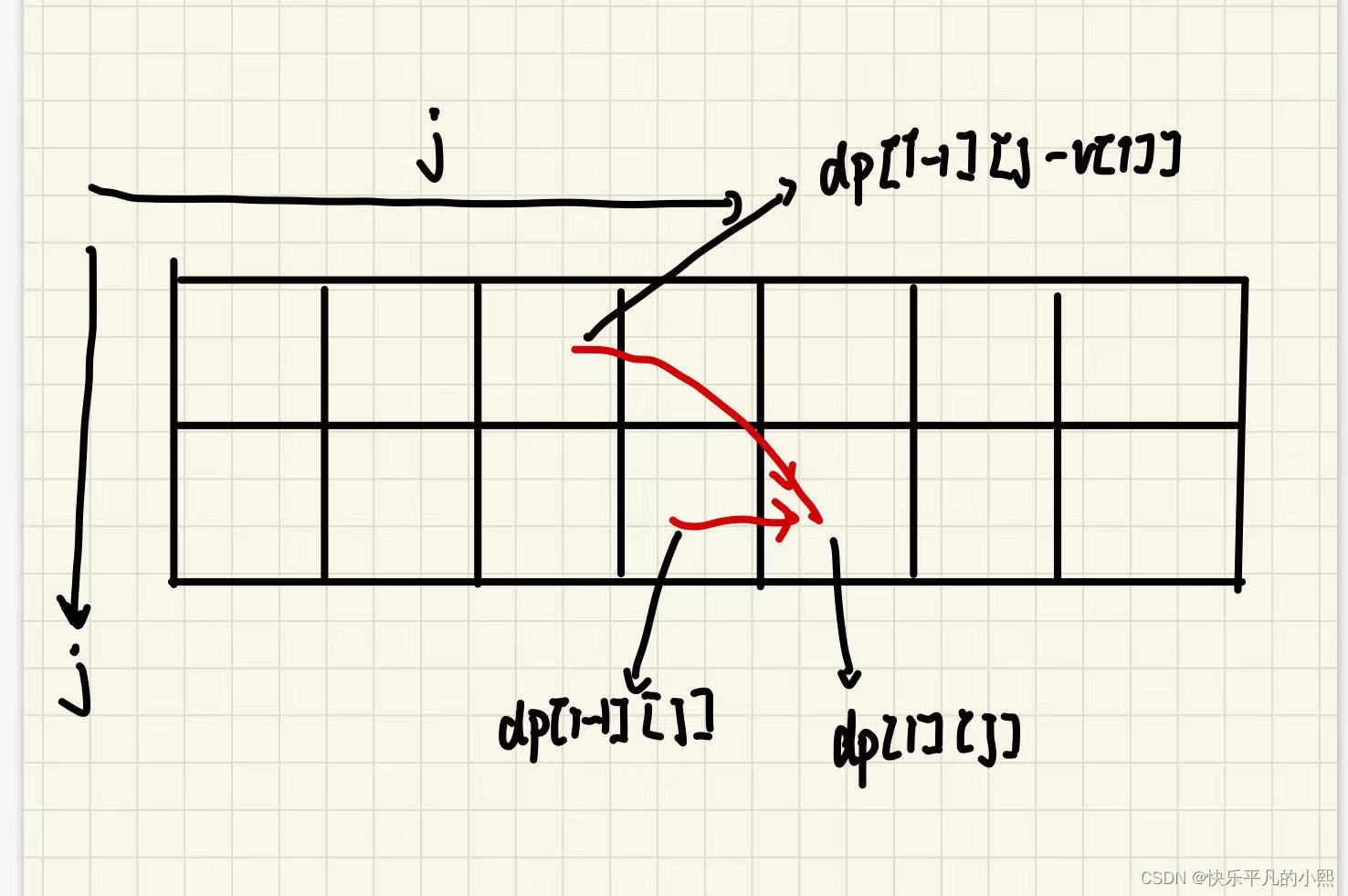
如图，dp数组更新的时候是前面的去更新后面的，这里需要保障前面的数组的值不发生变化，正序的话前面的数组的值就会被破坏了。 

#include
using namespace std;
const int N=1005;
int dp[N];
int v[N],w[N];
int n,m;
 
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>v[i]>>w[i];
	}
	
	for(int i=1;i<=n;i++)
	{
		for(int j=m;j>=v[i];j--)
		{
			if(j>=v[i]) dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
		}
	}
	
	cout<
	return 0;
}