前往我的主页以获得更好的阅读体验变限积分的导数 - DearXuan的主页https://blog.dearxuan.com/2022/08/08/%E5%8F%98%E9%99%90%E7%A7%AF%E5%88%86%E7%9A%84%E5%AF%BC%E6%95%B0/

积分上限函数

当定积分的上限为未知数x时，原定积分变成一个关于x的函数，称为积分上限函数

设

则

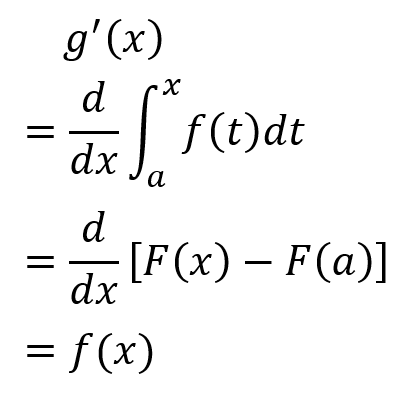
变限积分求导

设 f(x) 的原函数为 F(x)，且

则

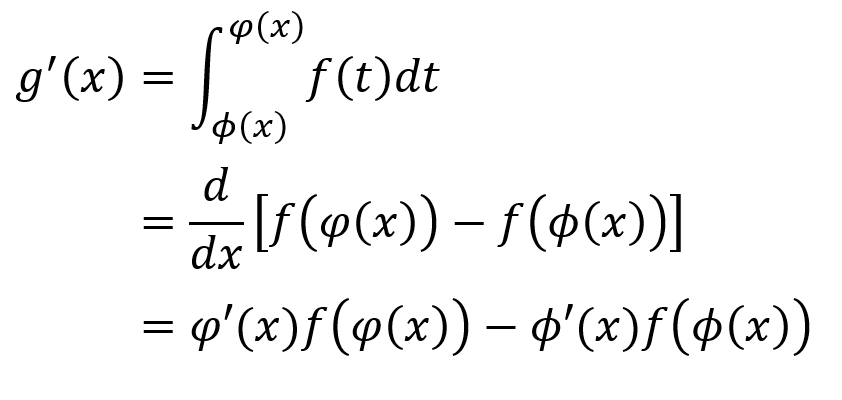
变限积分的无穷小阶数

设 f(x) 的原函数为 F(x)，且

对 g(x) 求导，得到

由于求导后阶数减一，因此 g(x) 的阶数为 (mn+n)

在实际做题时，可以通过等价无穷小或者泰勒展开的方法，将复杂的函数转化成多项式，因此该结论仍然成立，即 (被积函数的阶数+1) × 积分上限的阶数 

如下面函数的阶数就是 (2 + 1) × 1 = 3

当积分上下限都是函数但不是等价无穷小时，只需要将其看作两个积分上限函数相加即可。如果积分上下限是等价无穷小，那么需要特殊处理

由于上下限两个函数是等价无穷小，因此他们的最低阶数一定都是 Ax^n，即阶数相同，系数也相同，那么我们就可以将上限函数看作下限函数(最低阶为n)与另一个最低阶为k的多项式的和。换个说法，这个最低阶为k的多项式其实就是积分上下限之差，即上限减去下限

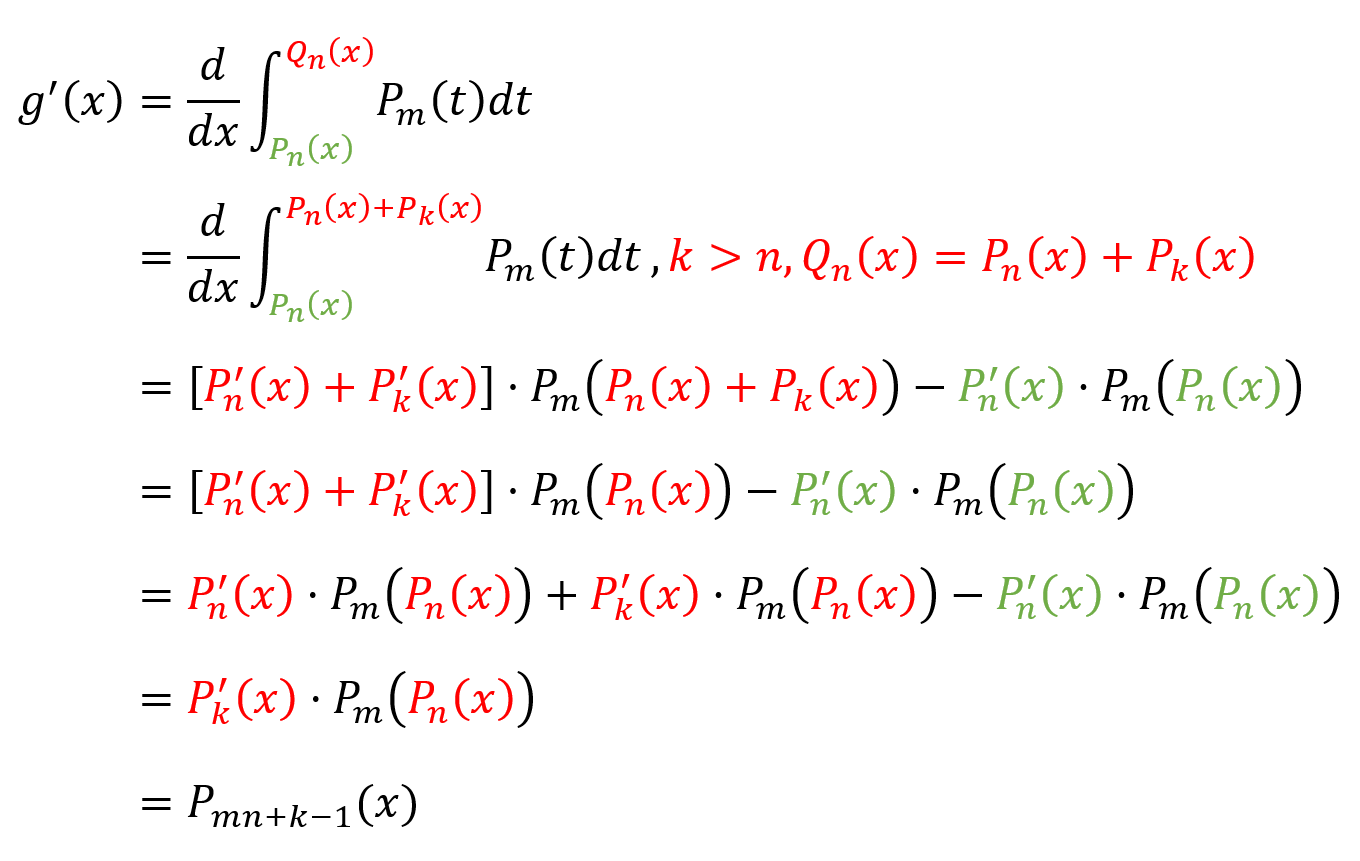
因此 g(x) 的阶数是 (mn+k)，即 被积函数的阶数 × 积分上(下)限的阶数 + 积分上下限之差的阶数

如下面函数的阶数是 1 × 1 + 3 = 4