LeetCode220807_73、旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

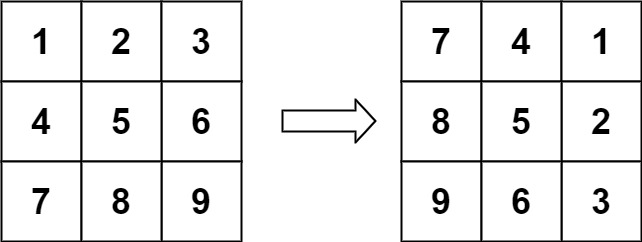
图1 旋转图像示例图

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/rotate-image
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解一、按行分析，旋转后的结果坐标和旋转前的元素坐标之间的关系，

第一行旋转为例，旋转后第一行到了倒数第一列，并且旋转前的列索引与旋转后的行索引一致。

即matrix[i][j] --->>> matrix[j][n - 1 - i]；

四次旋转（偶数行、列n/2，奇数行、列(n/2)，((n + 1) / 2)分配)，回归原点，具体详解请见。

旋转图像 - 旋转图像 - 力扣（LeetCode）

所以旋转后的：matrix[i][j]   旋转前的：matrix[n - 1 - j][i]；依次类推，直至回归原点。

class Solution{
    public void rotate(int[][] matrix){
        int n = matrix.length;
        for(int i = 0; i < n / 2; i++){
            for(int j = 0; j < (n + 1) / 2; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - 1 - j][i];
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
                matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
                matrix[j][n - 1 - i] = temp;
            }
        }
    }
}

题解二、先水平翻转、之后对角线翻转，可达同样效果

分析原因：水平翻转matrix[i][j] --->>> matrix[n - 1 - i][j]

之后进行，对角线反转matrix[n - 1 - i][j] --->>> matrix[j][n - 1 - i] 和题解一旋转结果相同。

class Solution{
    public void rotate(int[][] matrix){
        int n = matrix.length;
        for(int i = 0; i < n / 2; i++){
            for(int j = 0; j < n; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - 1 - i][j];
                matrix[n - 1 - i][j] = temp;
            }
        }
        for(int i = 0; i < n; i++){
            for(int j = 0; j < i; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}