SOM网络2： 代码的实现

SOM自组织映射神经网络的原理，详见博客：SOM网络1:原理讲解

训练的主函数

train_SO代码如下：

def train_SOM(X,                                                  # 输出节点行数
			  Y,                                                  # 输出节点列数
			  N_epoch,                                            # epoch
			  datas,                                              # 训练数据(N x D)  N个D维样本
			  init_lr=0.5,                                        # 初始化学习率  lr
			  sigma = 0.5,                                        # 初始化 sigma 用来更新领域节点权重
			  dis_func = euclidean_distance,                      # 距离公式  默认欧拉距离
			  neighborhood_func = gaussion_neighborhood,          # 邻域节点权重公式g  默认高斯函数
			  init_weight_fun=None,                               #初始化权重函数
			  seed=10):  			
	# 获取输入的特征维度
	N,D =np.shape(datas)
	# 训练的步数
	N_steps =N_epoch*N
	
	#对权重进行初始化
	rng = np.random.RandomState(seed)
	if init_weight_fun is None:
		weights =rng.rand(X,Y,D)*2-1                            #随机初始化
		weights /=np.linalg.norm(weights,axis=-1,keepdims=True) #标准化
	else:
		weights = init_weight_fun(X,Y,datas)                       # 一般使用PCA初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

PCA 初始化权重

def weights_PCA(X,Y,data):
	N,D=np.shape(data)
	weights=np.zeros([X,Y,D])
	pc_value,pc=np.linalg.eig(np.conv(np.transpose(data)))   # pc_vale为特征值,pc 为特征向量 DXD维
	pc_order=np.argsort(-pc_value)  # 特征值从大到小排序，并返回Index
	# 对W:[X,Y,D]进行初始化
	for i,c1 in enumerate(np.linspace(-1,1,X)):
		for j,c2 in enumerate(np.linsapce(-1,1,Y)):
			weights[i,j]=c1*pc[pc_order[0]]+c2*pc[pc_order[1]]   #利用最大的2个特征值对应的特征向量加权组合成i,j位置的D维表征向量	
1
2
3
4
5
6
7
8
9

完整的训练代码

def train_SOM(X,                                                  # 输出节点行数
			  Y,                                                  # 输出节点列数
			  N_epoch,                                            # epoch
			  datas,                                              # 训练数据(N x D)  N个D维样本
			  init_lr=0.5,                                        # 初始化学习率  lr
			  sigma = 0.5,                                        # 初始化 sigma 用来更新领域节点权重
			  dis_func = euclidean_distance,                      # 距离公式  默认欧拉距离
			  neighborhood_func = gaussion_neighborhood,          # 邻域节点权重公式g  默认高斯函数
			  init_weight_func=weights_PCA,                        #初始化权重函数
			  seed=10):  			
	# 获取输入的特征维度
	N,D =np.shape(datas)
	# 训练的步数
	N_steps =N_epoch*N
	
	#对权重进行初始化
	rng = np.random.RandomState(seed)
	if init_weight_func is None:
		weights =rng.rand(X,Y,D)*2-1                            #随机初始化
		weights /=np.linalg.norm(weights,axis=-1,keepdims=True) #标准化
	else:
		weights = init_weight_fun(X,Y,datas)                       # 一般使用PCA初始化
	
	for n_epoch in range(N_epoch):
		print("Epoch %d" %(n_epoch+1))
		#打乱样本次序
		index=rng.permulation(np.arange(N))
		for n_step,_id in enumerate(index):
			# 取一个样本
			x=datas[_id]
			#计算learning rate (eta)
			t=N*n_epoch + n_step
			eta=get_learning_rate(init_lr,t,N_steps)
			
			#计算样本距离输出的每个节点的距离，并获取激活点的位置
			winner=get_winner_index(x,weights,dis_func)
			
			#根据激活点的位置计算临近点的权重   随着迭代的进行sigma也需要不断减少
			new_sigma=get_learning_rate(sigma,t,N_steps)  # sigma 更新的方式和学习率一样
			g=neighborhood_fun(X,Y,winner,new_sigma) 
			g=g*eta
			
			#进行权重的更新
			weights =  weights + np.expand_dims(g,-1)*(x-weights)    
		
		# 打印量化误差
		print("quantization_error=%.4f" %(get_quantization_error(data,weights))) 
	return weights

#计算学习率
def get_learning_rate(lr,t,max_steps):  # t当前的steps   max_steps=N x epoch  (N样本数)		
	return lr/(1+t/(max_steps/2))	

# 获取激活(获胜点)节点的位置，与x距离最小的输出节点位置
def get_winner_index(x,w,dis_func=euclidean_distance):
	# 计算输入样本和各个节点的距离
	dis = dis_func(x,w)
	
	#找到距离最小的位置
	index=np.where(dis ==np.min(dis))
	return (index[0][0],index[1][0])

#利用高斯距离法计算临近点的权重
# X,Y模板大小,c中心点的位置  

def gaussion_neighborhood(X,Y,c,sigma)
	xx,yy=np.meshgrid(np.arange(X),np.arange(Y))
	d=2*sigma*sigma
	ax=np.exp(-np.power(xx-xx.T[c],2)/d)
	ay=np.exp(-np.power(yy-yy.T[c],2)/d)
	return (ax*ay).T

# 计算欧式距离
def euclidean_distance(x,w):
	dis=np.expand_dims(x,axis=(0,1))-w   # x:D w:[X,Y,D]  因此需要增加两维 x:D->x:[1,1,D]
	return np.linalg.norm(dis,axis=-1)                   # 输出[X,Y] 二范数 即为欧拉距离

# 特征标准化 (x-mu)/std
def feature_normalization(data):
	mu=np.mean(data,axis=0,keepdims=True)
	sigma=np.std(data,axis=0,keepdims=True)
	return (data-mu)/sigma

def get_U_Matrix(weights):
	X,Y,D=np.shape(weights)
	um=na.nan * np.zeros((X,Y,8))  #8 领域
	
	ii=[0 ,-1,-1,-1,0,1,1, 1]
	jj=[-1,-1, 0, 1,1,1,0,-1]
	
	for x in range(X):
		for y in range(Y):
			w_2=weights[x,y]
			
			for k,(i,j) in enumerate(zip(ii,jj)):
				if(x+i >=0 and x+i<X and y+j>=0 and y+j <Y):
					w_1=weights[x+i,y+j]
					um[x,y,k]=np.linalg.norm(w_1-w_2)
	um=np.nansum(um,axis=2)
	return um/um.max()

#计算量化误差   计算每个样本点和映射点之间的平均距离
def get_quantization_error(data,weights):
	w_x,w_y=zip(*[get_winner_index(d,weights) for d in datas])
	error=datas-weights[w_x,w_y]             # 数据域聚类中心的距离
	error=np.linalg.norm(error,axis=-1)  
	return np.mean(error)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107

训练完成后，返回输出节点的weights,维度为$[X,Y,D]$, 相当于固化了模型的权重weights, weights表征了当前的训练样本。

测试

if __name__ == "__main__":
	# seed 数据展示
	columns=['area','perimeter','compactness','length_kernel','width_kernel',
			'asymmetry_coefficient','length_kernel_groove','target']
	
	data = pd.read_csv('seeds_dataset.txt',names=columns,sep='\t+',engine='python')
	labs=data['target'].values
	lab_names={1:'Kama',2:'Rosa',3:'Canadian'}
	datas=data[data.columns[:-1]].values
	N,D=np.shape(datas)
	
	print(N,D)
	# 对训练数据进行标准化
	datas = feature_normalization(datas)
	
	#SOM的训练
	weights=train_SOM()X=9,Y=9,N_epoch=2,datas=datas,sigma=1.5,init_weight_func=weights_PCA)
	
	# 获取UMAP  用于可视化
	UM=get_U_Matrix(weights)
	plt.figure(figure=(9,9))
	plt.pcolor(UM.T,cmap='bone_r')  #plotting the distance map as background
	plt.colorbar()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

测试数据

U_Matrix

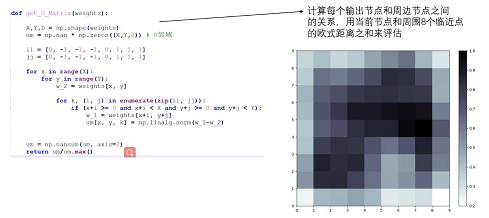
• 颜色越深说明与邻近点的关系越强烈，颜色越强说明与邻近点的关系越不强烈。

测试分类的效果

```python
if __name__ == "__main__":
	# seed 数据展示
	columns=['area','perimeter','compactness','length_kernel','width_kernel',
			'asymmetry_coefficient','length_kernel_groove','target']
	
	data = pd.read_csv('seeds_dataset.txt',names=columns,sep='\t+',engine='python')
	labs=data['target'].values
	lab_names={1:'Kama',2:'Rosa',3:'Canadian'}
	datas=data[data.columns[:-1]].values
	N,D=np.shape(datas)
	
	print(N,D)
	# 对训练数据进行标准化
	datas = feature_normalization(datas)
	
	#SOM的训练
	weights=train_SOM()X=9,Y=9,N_epoch=2,datas=datas,sigma=1.5,init_weight_func=weights_PCA)
	
	# 获取UMAP  用于可视化
	UM=get_U_Matrix(weights)
	plt.figure(figure=(9,9))
	plt.pcolor(UM.T,cmap='bone_r')  #plotting the distance map as background
	plt.colorbar()
	
   # 查看分类的效果
   markers=['o','s','D']
   colors =['C0','C1','C2']
   
   for i in range(N):
       x =datas[i]
       w=get_winner_index(x,weights)
       i_lab=labs[i]-1
	   plt.plot(w[0]+.5,w[1]+.5,markers[i_lab],markerfacecolor='None'
	           markeredgecolor=colors[i_lab],markersize=12,markeredgewidth=2)
   plt.show()	  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36