浅谈用匈牙利算法寻找二分图的最大匹配

一、匈牙利算法简介

匈牙利算法是由匈牙利数学家Edmonds于1965年提出。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。为了更好理解，先简单介绍一下二分图和最大匹配的概念，然后介绍算法思想，最后举例题说明。

二、二分图

二分图是图论中一种特殊的模型，设G = (V，E)是一个无向图，如果顶点V和E可分割为两个互不相同的顶点集（A，B）,并且图中的每条边线（Ax，By）所关联的两个顶点Ax和By分别属于A，B这两个顶点不同的顶点集，如下图所示。

三、最大匹配

图中没有任何一个同时连接Ax和By的同一顶点的时候我们称为二部图的一个匹配，也就是当A0与B0形成一个匹配后，那么B顶点集中的其他元素（B1、B2）不能与A0进行匹配，同时A顶点集中的其他元素（A1、A2、A3）不能与B0进行匹配。那么最大匹配就是图中能形成最多匹配的一种情况，如下图。

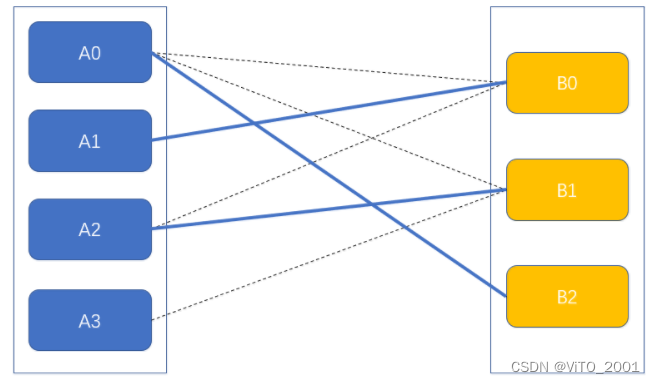
四、匈利亚算法思想

接下来将用一个的例子的推导过程浅析匈利亚算法的思想，给定如下二分图，推导能行成的最大匹配。

1. 定义从A顶点集匹配到B顶点集，那么最开始A0会与B0进行匹配

2. 下一步开始A1与顶点集B的匹配，由二分图可知A1能够与B0匹配，B0会查看自己已经与A0匹配，A0会从B顶点集查找自己还能与B1匹配，A0就会断开与B0的匹配并与B1建立新的匹配，断开的B0会与A1匹配。

3. 结束完A1的匹配，可以开始A2的匹配，A2首先会查看自己能够与B0建立匹配，B0会查看自己已经与A1匹配，A1就会寻找自己能够建立新的匹配；A2就会查找自己还可以与B1建立匹配，但是B1已经与A0建立匹配，A0就会查看自己会建立新的匹配（此时得注意刚刚A2已经与访问过B0得知不能建立匹配，A0就不能继续访问B0，不然又要毫无意义地问A1一遍），A0查找自己还能与B2进行匹配，那么A0就断开与B1的匹配与B2建立匹配，同时空出来的B1能够与A2建立匹配。

4. 最后开始A3的匹配，A3能够与B1建立匹配，但是B1已经与A2建立匹配（此时可以标记过访问过B1一次，避免再次访问）；A2查看自己能够与B0建立联系，但是B0已经与A1建立联系（此时可以标记过访问过B0一次，避免再次访问）；而A1除了B0外不能建立新的联系那么A3就不建立匹配。

5. 最后的最大匹配数是3
   

五、例题

例题来自牛客连接

描述

题目描述
若两个正整数的和为素数，则这两个正整数称之为“素数伴侣”，如2和5、6和13，它们能应用于通信加密。现在密码学会请你设计一个程序，从已有的 N （ N 为偶数）个正整数中挑选出若干对组成“素数伴侣”，挑选方案多种多样，例如有4个正整数：2，5，6，13，如果将5和6分为一组中只能得到一组“素数伴侣”，而将2和5、6和13编组将得到两组“素数伴侣”，能组成“素数伴侣”最多的方案称为“最佳方案”，当然密码学会希望你寻找出“最佳方案”。

输入:

有一个正偶数 n ，表示待挑选的自然数的个数。后面给出 n 个具体的数字。

输出:

输出一个整数 K ，表示你求得的“最佳方案”组成“素数伴侣”的对数。

数据范围： 1 \le n \le 100 \1≤n≤100 ，输入的数据大小满足 2 \le val \le 30000 \2≤val≤30000

输入描述：

输入说明
1 输入一个正偶数 n
2 输入 n 个整数

输出描述：

求得的“最佳方案”组成“素数伴侣”的对数。

示例1

输入：

4
2 5 6 13
1
2

输出：

2
1

示例2

输入：

2
3 6
1
2

输出：

0
1

分析

由于偶数+偶数=偶数，不是素数；奇数+奇数=偶数，不是素数，所以只有奇数+偶数才有可能形成素数，则可以把输入的整数分为奇数和偶数两类，进而构成二分部，用匈利亚算法求解。这里附上源码（已添加注释）。

源码

#include
#include
using namespace std;

//判断一个整数是否为素数
bool IsPrime(int num);
//判断第odd位奇数能够与偶数建立联系
bool BuildRelation(int odd,vector<int> even,vector<vector<bool>>map,vector<bool> &visited,vector<int> &target);

int main()
{
    int n;//输入整数的个数
    vector<int> odd,even;//定义容器存放奇数、偶数
    cin >> n;
    for(int i = 0; i < n; i++)//将输入的整数进行奇偶分类
    {
        int tempint;
        cin>>tempint;
        if(tempint % 2 == 0) even.push_back(tempint);
        else odd.push_back(tempint);
    }
    if(even.empty() || odd.empty())//如果有个奇数容器或偶数容器为空，那么最大匹配为0
    {
        cout << 0;
        return 0;
    }
    vector<vector<bool>> map(odd.size(),vector<bool>(even.size(),0));//定义大小为（odd.size()，even.size()）的容器，存放二分图内部联系
    for(int i = 0 ;i < odd.size() ;i++ )//建立二分图内部的联系，确认哪些元素可以互相建立联系
    {
        for(int j = 0 ; j < even.size() ;j++)
        {
            map[i][j] = (IsPrime(odd[i] + even[j]));
        }
    }
    vector<int> eventarget(even.size(),-1);//保存偶数已经与哪个奇数匹配，存放数值位该奇数在奇数容器中的位置
    vector<bool> oddvisit(even.size(),0);//保存每次访问过哪些偶数
    int count = 0;//统计最大匹配
    for(int i = 0 ;i < odd.size() ;i++ )//遍历奇数容器元素
    {
        for(int j = 0 ; j < even.size() ; j++ ) oddvisit[j] = 0;//清空上次访问过的偶数
        count += BuildRelation(i,even,map,oddvisit,eventarget);
    }
    cout << count<<endl;
    return 0;
}

//传入一个整数
bool IsPrime(int num)
{
    for(int i = 2; i * i <= num ;i++)
    {
        if(num % i == 0) return false;//不是素数
    }
    return true; //是素数
}

//传入某个奇数的位次，偶数组，二分图，以及标志造访过的数组，偶数已经与哪个奇数建立联系的数组
bool BuildRelation(int odd,vector<int> even,vector<vector<bool>>map,vector<bool> &visited,vector<int> &target)
{
    for(int i = 0 ; i < even.size();i++)//与偶数容器中的每个元素进行判断
    {
        if(map[odd][i] && !visited[i])//二分图中该奇数与该偶数能建立联系  &&   本次判断中没有访问过该偶数
        {
            visited[i] = true;//访问标记
            if(target[i] == -1 || BuildRelation(target[i],even,map,visited,target) ) //该偶数没有进行匹配   ||  与该偶数建立联系的奇数能找到新的匹配              
            {
                target[i] = odd;//标记该偶数与该奇数建立匹配
                return true;//能够匹配放回1
            }
        }
    }
    return false;//不能匹配返回0
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73