习题 --- 双指针算法、离散化

 数组元素的目标和

给我们两个有序的序列和一个目标值，数组下标从 0 开始，让我们找到一个数对 i、j，使得 A[ i ] + B[ j ] = x，数据保证只有一组解，这是一个经典的双指针算法，接下来回忆一下双指针算法的基本考虑思路    双指针算法、位运算、离散化、区间合并

第一步先想一下暴力怎么做，然后对暴力做优化就可以了，i 从 0 枚举第一个数组，j 从 0 枚举第二个数组，如果 ai + aj = x 就输出答案，i 计算了 n 次，j 计算了 nm 次，整个算法的时间复杂度为 O(nm)

接下来看一下如何优化：双指针算法的优化其实就是找单调性，可以发现 a 数组和 b 数组都是单调上升的，对于每一个 i 而言，都在 b 数组里面找一个 j，使得 ai + bj ≥ x，而且 j 最小( j 是最靠左的一个)，可以发现这样就具有单调性了，当 i 往后移动的过程中，j 一定是往前移动的，因为总和 x 是不变的，i 变大之后，j 一定会变小

由于 a、b 两个数组是单调的，找到单调性后，就可以用双指针算法解决这道题目

时间复杂度分析

暴力做法时间复杂度妥妥 O()

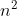双指针算法中的 i 一共循环 n 次，j 初始的时候等于 m，每一次都会减减，最多会减到 0，因此 j 循环了 m 次，两个加在一块就是 O(n + m) 次

模拟样例

i 指针一开始指向 A 的第一个位置，目标值是 6，j 一开始指向 B 的最后一个位置，只要 ai + bj ＞ 6，j 就一直 - -，i = 1，j = 4；i = 2，j = 4，这样就找到答案了，可以 break

离散数学《第二版》习题解答

application/x-zip 5星 超过95%的资源 333KB

下载

可以发现当 i 从前往后移动的时候，j 是从后往前移动的，当它们的和等于 6 的时候就停止

以上就是本道题目的基本思路，总的来说双指针算法都是先把暴力的做法写出来，然后看一下有没有单调性，如果有单调性的话，我们就可以利用单调性把时间复杂度降低一维

#include 
#include 
 
using namespace std;
 
const int N = 100010;
 
//n、m表示两个数组的元素个数
int n, m, x;
//a、b表示两个数组
int a[N], b[N];
 
int main()
{
    //读入数组长度以及目标值
    scanf("%d%d%d", &n, &m, &x);
    //读入a数组里面的每一个数
    for(int i = 0; i < n;i++ ) scanf("%d", &a[i]);
    //读入b数组里面的每一个数
    for(int i = 0; i < n;i++ ) scanf("%d", &b[i]);
 
    //用两个指针来扫描 初始的时候j应该等于最后一个元素
    for(int i = 0, j = m - 1;i < n;i++ )
    {
        //j没有出界并且a[i] + b[j] > x
        while(j >= 0 && a[i] + b[j] > x) j -- ;
        //如果a[i] + b[j] = x就把下标输出
        if(a[i] + b[j] == x) printf("%d %d\n", i, j);
        //由于题目保证了只有一组解所以可以不用break 当然也可以break
        break;
    }
    return 0;
}

如果有多组答案应该怎么思考呢？

a = {1，1，1，1，1}，b = {1，1，1，1，1}，需要满足和等于 2，一共有多少组解呢？一共就是 n × m 组解，整个算法的时间复杂度就是 O()

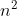区间和

给出一个无限长的数轴，数轴的范围：-10^9 ~ 10^9，数轴上每个坐标上的数一开始都是 0，现在要进行 n 次加法操作，每次操作是将某个位置 x 上的数加上 c，再进行 m 次询问操作，每次询问两个整数之间所有数的和，操作、询问的坐标都是 10^9 级别，但是操作的数量只有 10^5 级别，快速求区间和可以用前缀和，但是前缀和中需要把值当作下标来做，例如：如果想求 l 到 r 之间所有数的和，需要用 SR - SL-1，把值当作下标，但是 l 和 r 的值都是在 10^9 级别的，不可能把一个规模是 10^9 的一个数当作下标，数组是开不了这么大的，此时就可以用离散化来做

离散化的思想是：把所有用到的下标放到数组里面去，离散化的核心思想就是把所有用到的数排序、判重，离散化的方式就是用它的下标来表示它原来的值，查询操作可以用二分或者 lower_bound( )

关于lower_bound( )和upper_bound( )的常见用法

双指针算法、位运算、离散化、区间合并

find 函数的本质是寻找 x 离散化之后的值是什么，用下标来做离散化之后的结果，因为下标是连续的，由于需要用到前缀和，下标从 1 开始

//求 x 这个值离散化后的结果
int find(int x) 
{
    int l = 0,r = alls.size() - 1;
    while(l < r)
    {
        //取中点
        int mid = l + r >> 1;
        //找大于等于 x 的最小的数
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    //返回位置的下标 + 1  把 x 映射到从 1 开始的自然数-> 前缀和不需要处理边界
    return r + 1;  
}
 
int find(int x) 
{
    return lower_bound(alls.begin(), alls.end(), x) - alls.begin() + 1;
}

之后再把原来的值换成离散化之后的值，离散化的作用就是把范围 10^9 【规模比较大的数】变成 3 × 10^5 【规模比较小的数】以内的数，然后就可以用前缀和算法来解决这个问题了