计数与期望

目录

组合数

卡特兰

---

组合数

对于方程：,求有多少组非负整数解。正常插板法只适用于正整数解，两个板不能插到一个空里，为了解决这个问题我们在方程左右同时加上k，得到答案 C(n+k-1,k-1)；

Count the Arrays 

    (n-2)指减去一个中间的最大值与一个重复值，2^(n-3)指在把数字分别放到最大数两边，此时已经有3个数字（最大值、两个相同的数——一左一右）确定下来

#include
using namespace std;
#define int long long
const int mod=998244353;
int n,m;
int qp(int a,int b)
{
	int res=1;
	while(b)
	{
		if(b&1) res=res*a%mod;
		b>>=1;
		a=a*a%mod;
	}
	return res;
}
signed main()
{
	scanf("%lld%lld",&n,&m);
	if(n==2)
	{
		printf("0");
		return 0;
	}
	int nn=1,mm=1;
	for(int i=m;i>=m-n+2;i--) nn=nn*i%mod;
	for(int i=1;i
	printf("%lld",nn*qp(mm,mod-2)%mod*qp(2,n-3)%mod*(n-2)%mod);
	return 0;
}

卡特兰

应用：进出栈、二叉树

其实大概可以抽象成：满足…序列中…的个数都不少于…的个数的序列有多少个

[HNOI2009]有趣的数列 

呃其实挺苟的 在正常处理卡特兰的时候还要处理取模，题目没有保证模是质数，我们采用分解质因数（快速幂）来处理（逆元都没法用qwq)。上下质因数的指数相减就除完了。

#include
using namespace std;
#define int long long
int n,p,ans,cnt;
int prime[5000010],vis[5000010];
void get_prime(int n)
{
	for(int i=2;i<=n;i++)
	{
		if(!vis[i]) prime[++cnt]=i;
		for(int j=1;i*prime[j]<=n;j++)
		{
			vis[i*prime[j]]=1;
			if(i%prime[j]==0) break;
		}
	}
}
int quickpow(int aa,int bb)
{
	int res=1;
	while(bb)
	{
		if(bb&1) res=aa*res%p;
		bb>>=1;
		aa=aa*aa%p;
	}
	return res;
}
int calc(int aa,int bb)
{
	int res=0;
	while(aa)
	{
		aa/=bb;
		res+=aa;
	}
	return res;
}
int China(int aa,int bb)
{
	int res=1,x,y;
	for(int i=1;i<=cnt;i++)
	{
		int pap=prime[i];
		int a=calc(aa,pap);
		int b=calc(bb,pap);
		int c=calc(aa-bb,pap);
		res=res*quickpow(pap,a-b-c)%p;
	}
	return (res+p)%p;
}
signed main()
{
	scanf("%lld%lld",&n,&p);
	get_prime(n*2);
	printf("%lld",(China(n*2,n)-China(2*n,n-1)+p)%p);
	return 0;
}

容斥

我就不是很理解为什么看起来非常友善的容斥在c++里这么难推式子

[SCOI2010]幸运数字 

#include
using namespace std;
#define int long long
int a,b,ans,cnt=2,tot;
int num[100010],k[100010];
bool vis[1000010];
int gcd(int aa,int bb)
{return bb==0?aa:gcd(bb,aa%bb);}
void dfs(int now,int x,int sum)
{
	if(now==0)
	{
		int cntt=b/x-a/x;
		if(sum&1) ans-=cntt;
		else ans+=cntt;
		return;
	}
	dfs(now-1,x,sum);
	double tmp=x/gcd(x,k[now]);
	if(tmp*k[now]<=b) dfs(now-1,x/gcd(x,k[now])*k[now],sum+1);
}
signed main()
{
	scanf("%lld%lld",&a,&b);
	num[1]=6,num[2]=8;
	for(int i=1;num[i]<=b;i++)
	{
		num[++cnt]=num[i]*10+6;
		num[++cnt]=num[i]*10+8;
		while(num[cnt]>b) cnt--;
	}
	for(int i=1;i<=cnt;i++)
	{
		if(!vis[i])
		{
			k[++tot]=num[i];
			for(int j=i+1;j<=cnt;j++)
				if(num[j]%num[i]==0)
					vis[j]=1;
		}
	}
	ans=b-a+1,a--;
	dfs(tot,1,1);
	printf("%lld",ans);
	return 0;
}

对于容斥，有一些真正会用到的要点，或者说是推式子的步骤：

1. 根据题目确定要统计、排列组合的元素-->”钦定“
2. 计算该元素会被统计多少次，同时计算它对答案的贡献
3. 容斥进行简单的加减计算 / 枚举子集

对于大部分容斥题目来说，经常会用到两个式子

 

这里我们用到的是第二个式子：当统计钦定的m个幸运数的倍数的个数时，每一个数会被统计次，对答案的贡献是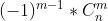,即如果其是至少一个幸运数的倍数则会被统计一次，否则不被统计。

那么这里的±1是怎么出来的呢？

方法一：

杨辉三角性质：

方法二：

刷表

我们要做的事情就是求一些物品x在条件C下的贡献,所谓容斥就是指我们从所有X值里找到相对好求的值，再对每个条件构建一个系数，构成式子

          其中f[i]由DP打表找规律得（？？？）