-
【DR_CAN-MPC学习笔记】1.最优化控制和MPC基本概念
准研一,准备做混动方向,先学一下MPC相关知识
DR_CAN的视频:【MPC模型预测控制器】1_最优化控制和基本概念:
【MPC模型预测控制器】1
1.最优化控制 Optimal Control
最优化控制的目的 Motivation:
在约束条件下达到最优的系统表现 Get the best performance within certain limitation- 约束条件:物理限制等等;
- 最优:综合分析的结果,不是绝对的。举个例子:汽车变道的轨迹选择

如上图所示,有两条线路可以选择,红色的线路1行驶距离短,速度快,较为舒适,绿色的线路2考虑到了紧急避障,需要迅速变道。因而在这个问题中,最优结果是相对的,不是绝对的。
2.数学模型 Mathematical Model
将上述的车辆行驶轨迹用数学模型表示。
2.1 SISO模型
SISO (Single Input Single Output,单输入单输出) 用以下系统框图表示:

r(t):系统参考值
u(t):输入
y(t):输出
e(t):误差 e(t) = y(t) - r(t)从轨迹追踪的角度来看:
 越小,跟踪效果越好(误差越小)
越小,跟踪效果越好(误差越小) 越小,输入越小(输入越小)
越小,输入越小(输入越小)引入代价函数(Cost Function):

最优化的过程即设计控制器的
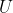 ,使得
,使得 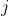 取得最小值
取得最小值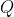 和
和 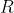 均为调节参数,
均为调节参数,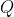

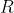 时,更看重误差,
时,更看重误差,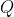

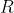 时,更看重能耗。
时,更看重能耗。2.2 MIMO模型
再扩展至MIMO(Multiple Input Multiple Output,多输入多输出)用状态空间表示:

例:
参考值
![\begin{array}{l} V = \left[\begin{array}{l} v_{1} \\ v_{2} \end{array}\right] = \left[\begin{array}{l} 0 \\ 0 \end{array}\right] \\ \end{array}](https://1000bd.com/contentImg/2022/07/27/184219168.gif)
误差
![E = \left[\begin{array}{l} e_{1} \\ e_{2} \end{array}\right] = \left[\begin{array}{ll} y_{1}-r_{1} \\ y_{2}-r_{2} \end{array}\right] = \left[\begin{array}{l} x_{1} \\ x_{2} \end{array}\right]](https://1000bd.com/contentImg/2022/07/27/184220375.gif)
其中
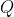 和
和 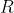 是调节矩阵,
是调节矩阵, 、
、 、
、 、
、 为调节系数。
为调节系数。3.模型预测概念
通过模型来预测系统在某一未来时间段内的表现来进行优化控制。
注:多用于数位控制,多采用离散型状态空间表达式,即
离散时采用欧拉法
(在k时刻)
步骤:
Step1:估计/测量读取当前系统状态(可测量则测量,不可测量则估计)Step2:基于
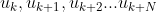 进行最优化
进行最优化如下图所示:
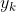 ~
~  预测区间 Predictive Horizon
预测区间 Predictive Horizon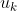 ~
~  控制区间 Control Horizon
控制区间 Control Horizon 的选取即为最优化问题
的选取即为最优化问题
代价函数
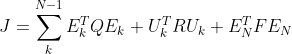
 表示最终代价(预测时间最末端误差的代价) Terminal Cost
表示最终代价(预测时间最末端误差的代价) Terminal Cost
Step3:只取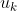 (只选取
(只选取 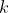 时刻作为预测结果,因为预测存在局限性)
时刻作为预测结果,因为预测存在局限性)
在预测 点的时候,预测区间和控制区间向右移动一时刻,以此预测未来的表现,这个过程叫做滚动优化控制 Receding Horizon Control
点的时候,预测区间和控制区间向右移动一时刻,以此预测未来的表现,这个过程叫做滚动优化控制 Receding Horizon Control
MPC特点:- 在每一步都需要进行十次最优化计算,因此对控制器计算能力要求较高
- 求解最优化问题时,会考虑系统的约束
-
相关阅读:
Python每日一练(牛客数据分析篇新题库)——第31天:中位函数
神经元网络技术有限公司,神经网络网站
使用Vue3封装的切换主题开关
网络设备和网络软件
JVM本地方法栈介绍
MySQL的自增id会用完吗?用完怎么办?
【开源讲解】
中国单反相机行业供需趋势及投资风险研究报告
第2章 内容管理模块v3.1
共模电感选择请收好谷景电感教你的小方法
- 原文地址:https://blog.csdn.net/weixin_43470383/article/details/125883376