二叉树的概念

在计算机科学中，二叉树是每个节点最多有两个子树的树结构。二叉树可以为空树，通常子树被称为”左子树“和”右子树“
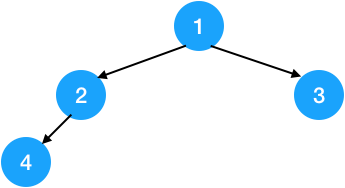
比如下图就是一棵二叉树

二叉树的每个节点最多有两棵子树（不存在度大于2的节点），二叉树的子树有左右之分，次序不能颠倒
二叉树的第i层，最多有$2^{i-1}$个结点
深度为k的二叉树，最多有$2^k-1$个结点
对于任何一颗二叉树，如果其叶结点数为$n0$，度为2的节点数为$n2$，则$n0=n2+1$
对于最后一个结论可以这么理解，当我们给某个节点新增一个子节点时，如果原节点度数为0则原节点为叶节点，添加后原节点度数为1，新节点为叶节点，所以$n0$和$n2$都不变
如果原节点度数为1，添加后原节点度数为2，$n2$会增加1，新增的节点为叶节点，所以$n0$也会增加1，该等式仍然成立

特殊的二叉树

满二叉树

一棵深度为k，且有$2^k-1$个结点的二叉树，成为满二叉树。满二叉树每一层的结点都是满的
如下图

完全二叉树

在一棵二叉树中，除了最后一层外，其余层都是满的，或者是在右边缺少连续若干结点，则此二叉树为完全二叉树。具有n个结点的完全二叉树的深度是$log(n+1)$。深度为k的完全二叉树，至少有$2^{k-1}$个结点，最多有$2^k-1$个结点
如下图

满二叉树也是完全二叉树的一种

排序二叉树

排序二叉树(Binary Search Tree,BST)，又称二叉排序树，二叉查找树，具有下列的特质

1. 若左子树不空，则左子树上所有结点的值均小于它的根结点的值
2. 若右子树不空，则右子树上所有结点的值均大于它的根结点的值
3. 左、右子树也分别为排序二叉树

排序二叉树也可以是空树
一般情况下排序二叉树所有结点的值不同，如果需要考虑重复的值，可以另加一个数组$cnt$记录BST每个结点的值的个数

二叉树的存储

和一般的树不同，二叉树的子结点分为左儿子和右儿子，左儿子和右儿子均可能为空
我们用一个数组son来存储一棵二叉树，son[u][0]表示u结点的左儿子，son[u][1]表示u结点的右儿子，值为0表示空

如上图，存储的代码为

root = 7;
son[7][0] = 1;
son[7][1] = 6;
son[1][1] = 4;
son[4][0] = 3;
son[4][1] = 2;
son[6][0] = 5;
1
2
3
4
5
6
7

二叉树的遍历

在二叉树中，因为左右孩子不同，所以很少进行深度优先搜索和广度优先搜索，一般进行几种特殊的遍历：先序遍历、中序遍历、后序遍历和层次遍历

先序遍历

在对二叉树遍历时，先访问当前子树的根节点，再依次访问左子树和右子树。
如上图先序遍历为7 1 4 3 2 6 5

中序遍历

在对二叉树进行遍历时，先访问当前子树的左子树，再访问子树的个节点，最后访问当前子树的右子树
如上图中序遍历为1 3 4 2 7 5 6

后序遍历

在对二叉树进行遍历时，先依次访问当前子树的左右子树，最后访问当前子树的根结点
如上图后序遍历为3 2 4 1 5 6 7

层次遍历

在对二叉树进行遍历时，按从左到右依次遍历从上到下每一层的结点。层次遍历类似于广度优先搜索，但是对于同一层的结点，顺序必须为从左到右，可以借助队列实现
如上图的层次遍历为7 1 6 4 5 3 2

特殊地，对于排序二叉树，它的中序遍历结果为这些数的排序结果

二叉树的四种遍历的代码

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int N = 1005;
vector<int> v1, v2, v3, v4;
int son[N][2],root;
void build() {
    root = 7;
    son[7][0] = 1;
    son[7][1] = 6;
    son[1][1] = 4;
    son[4][0] = 3;
    son[4][1] = 2;
    son[6][0] = 5;
}
void print() {
    cout << "preorder:";
    for (int i = 0; i < v1.size(); i++) {
        cout << v1[i] << " ";
    }
    cout << endl;
    cout << "inorder:";
    for (int i = 0; i < v2.size(); i++) {
        cout << v2[i] << " ";
    }
    cout << endl;
    cout << "postorder:";
    for (int i = 0; i < v3.size(); i++) {
        cout << v3[i] << " ";
    }
    cout << endl;
    cout << "levelorder:";
    for (int i = 0; i < v4.size(); i++) {
        cout << v4[i] << " ";
    }
    cout << endl;
}
void preorder(int u){
    if(u==0)
        return;
    v1.push_back(u);
    preorder(son[u][0]);
    preorder(son[u][1]);
}
void inorder(int u){
    if(u==0)
        return;
    inorder(son[u][0]);
    v2.push_back(u);
    inorder(son[u][1]);
}
void postorder(int u){
    if(u==0)
        return;
    postorder(son[u][0]);
    postorder(son[u][1]);
    v3.push_back(u);
}
void levelorder(){
    queue<int> q;
    if(root!=0)
        q.push(root);
    while(!q.empty()){
        int u=q.front();
        q.pop();
        v4.push_back(u);
        if(son[u][0]!=0)
            q.push(son[u][0]);
        if(son[u][1]!=0)
            q.push(son[u][1]);
    }
}
int main() {
    build();
    preorder(root);
    inorder(root);
    postorder(root);
    levelorder();
    print();
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82