Lyapunov稳定性分析2（连续、离散系统）

一、李雅普诺夫第一方法（间接方法）

线性系统，只须求出系数矩阵的特征值即可判断其稳定性（见作者”控制系统分析1（线性系统稳定性和收敛性）”博客）；
非线性系统，则由若干过程组成，其中每个过程都要用到具体的形式。

二、李雅普诺夫第二方法

李雅普诺夫第二方法：又称直接法，其基本特点是不必求解系统的状态方程，就能对其在平衡点处的稳定性进行分析和做出判断，且这种判断是准确的，而不包含近似。
　　李雅普诺夫稳定性理论建立了系统能量与稳定性之间的关系：如果系统有一个渐近稳定的平衡状态，则当它转移到该平衡状态的邻域内时，系统所具有的能量随着时间的增加而逐渐减少，直到在平衡状态达到最小值。需要有一个抽象的能量函数来描述系统的虚拟能量。
　　能量函数：状态和时间的标量函数，又称为李雅普诺夫函数，记作V(x,t)。

三、李雅普诺夫稳定性判定

1. 线性定常系统：　　

（1）Lyapunov渐近稳定的充要条件（第一方法）：A的特征值全部在左半平面
（2） Lyapunov渐近稳定的充要条件（第二方法）：对于任意的正定矩阵Q，存在正定矩阵P满足Lyapunov方程：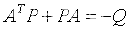
（3）MATLAB函数判断Lyapunov稳定性
Example1：MATLAB自带的例子

系统矩阵A的特征值均小于0，所以该系统稳定，Lyapunov方程有解

Example2：

系统矩阵A存在一个特征值大于0，所以该系统稳定，Lyapunov方程无解。