简易入手《SOM神经网络》的本质与原理

简易入手《SOM神经网络》的本质与原理
原创文章，转载请说明来自《老饼讲解神经网络》:bp.bbbdata.com

关于《老饼讲解神经网络》：

本网结构化讲解神经网络的知识，原理和代码。

重现matlab神经网络工具箱的算法，是学习神经网络的好助手。

目录

一、入门原理解说

01. 基于Kohonen规则的聚类算法

02.  SOM聚类的思想

03.  SOM神经网络的拓扑图

04.  SOM的模型表达式

编后语

二、SOM-代码重写(单样本训练)

01. 代码结构说明

02. 代码运行结果解说

03. 具体代码

SOM神经网络(Self-organizing Feature Map)是Kohonen在1981年提出的一种用于聚类的神经网络，是神经网络家族中经典、重要且广泛应用的一员。

本篇第一节先聚焦于讲清SOM是个什么东西，解决什么问题，思路是什么，有什么特性，
第二节则扒取matlab的源码，自写《SOM-单样本训练算法》，即用自己的代码逻辑重现matlab工具箱的效果。

  笔者语

SOM不是一个困难的算法，但要讲清SOM,却是一个困难的问题。

笔者曾想一张文章讲完SOM，左揉右捏，后来发现，这鬼东西，越图快越不行。

为什么SOM必须慢慢讲述，主要是因为SOM的思想经历了三阶段：

  Kohonen规则   -->   单样本训练   -->   批量样本训练

想直接讲述批量样本训练根本讲不了。

谨此，希望读者也不要图快，一步一步来。

一、入门原理解说

  01. 基于Kohonen规则的聚类算法

  聚类问题

口语描述：假设数据是一团团的，我们希望找出这些一团团数据的中心点(聚类中心)，样本离哪个聚类中心最近，就将样本判为该聚类中心。

   基于Kohonen规则的聚类方法

kohonen规则聚类很简单，

先随机初始化k个聚类中心点，

然后每次选出一个样本，将离它最近的聚类点往它移动，使该聚类点更靠近它，如此反复m次。

更新法则如下：

$w_{k} = w_k+\text{lr}*(x-w_k)$

其中，
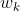：离样本最近的聚类中心点。
$\text{lr}$ : 学习率。

   kohonen规则的有效性

kohonen规则虽然简单，然而它却是行之有效的。

且看一个Demo：

平面中有四簇数据，
我们先随机初始化5个聚类中心点，
然后使用Kohonen规则调整聚类中心点的位置，

可以看到，经过一定步数后，聚类中心点移到了四类数据的中心位置附近。

Demo代码：
```
% Kohonen聚类规则
rand('seed',70);
%------------生成样本数据-------------
dataC = [2.5,2.5;7.5,2.5;2.5,7.5;7.5,7.5]; % 生成四个样本中心
sn = 40;  % 样本个数
X = rand(sn,2)+dataC(mod(1:sn,4)+1,:); % 随机生成样本点
 
 
% -----------初始化聚类中心点--------------
kn = 5;              % 聚类中心点个数
C  = rand(kn,2)*10;  % 随机生成聚类中心
C0 = C;              % 备份聚类中心点的初始值
 
 
% -----------使用样本训练聚类中心点-----------
lr = 0.1;   % 学习率
for t = 1:50
    for i = 1:sn
        cur_x    = X(i,:);                             % 提取一个样本
        dist     = sum((repmat(cur_x,kn,1) - C).^2,2); % 计算样本到各个聚类中心点的距离
        [~,idx]  = min(dist);                          % 找出最近的聚类中心点
        C(idx,:) = C(idx,:)  + lr*(cur_x - C(idx,:));  % 将该聚类中心点往样本靠近
    end
end
 
 
% ----------画图------------------------
subplot(1,2,1)
plot(X(:,1),X(:,2),'*');
hold on 
plot(C0(:,1),C0(:,2),'or','MarkerFaceColor','g');
 
 
subplot(1,2,2)
plot(X(:,1),X(:,2),'*');
hold on 
plot(C(:,1),C(:,2),'or','MarkerFaceColor','g');
```
  02.  SOM聚类的思想

SOM是Kohonen规则的改进，

它在更新离样本最近的聚类中心点P的的时候，会把P的邻近聚类中心点也一起更新。

请注意，初学者很容易误会，以为SOM所指的邻近聚类点就是目标聚类点附近的聚类点，其实不是，SOM对“邻近聚类点”有自己的定义。

  SOM聚类点的距离与邻近聚类点

SOM是先引入一个拓扑结构，把所有聚类点连结在一起，然后籍此来定义距离。

拓扑结构

拓扑结构可以是一维的，二维的，三维的，等等，最常用是二维
例如最常用的二维六边形拓扑结构：

距离的定义

在SOM中，两点之间的距离，
是指在引入的拓扑结构中，这两点之间的最小边数。

邻近聚类点

点P的邻近聚类点是指与P的最小连结边数小于某个阈值的聚类点。
例如，
当邻域距离阈值为1时，点P的邻近聚类点，是与点P直接连接的点。
当邻域距离阈值为2时，则是到达点P不超过2条边的聚类点。
当邻域距离阈值为k时，就是指经过m（m<=k)条边可达点P的聚类点。

  SOM的更新方法

SOM更新的方法与上面所说的Kohonen规则思想是一样的，
不同点在于，SOM在更新离样本最近的聚类中心点P的的时候，会把P的邻近聚类中心点也一起更新


更细节的，有以下三点：

1、更新邻近聚类点：
更新样本最近点P的同时，P的邻近聚类点也一起更新，(P的学习率要比邻近聚类点更大一些)。

2、增加学习率的收缩机制：
随着更新步数，学习率越来越小。

3、邻近距离收缩机制：
随着更新步数，邻近距离阈值越来越小，渐渐的，只有目标点及其邻边聚类点。

比起纯粹的Kohonen规则，虽然改动不大，在代码编写上，却要复杂很多。
复杂是因为要初始化拓扑结构，获得点与点之间的距离矩阵(这里说的距离是上面所说的边数)，以便在更新时获取邻近聚类点。

   说明

●  以上的更新方法来自matlab老版本的单样本训练算法(learnsom)。
●  matlab新版本已采用了批量更新算法(learnsomb)。
两种方法的细节，我们都另起文章细讲，并扒出源码，重现matlab的实现逻辑。



  03.  SOM神经网络的拓扑图

  网络拓扑图

SOM神经网络是典型的三层神经网络，
拓扑图如下：

第一层是输入层
第二层是隐层，
隐层有多少个隐节点，就代表有多少个聚类中心点 ( 聚类中心点的位置就是该隐节点与输入的连接权重 ) 。
第三层是输出层
输出层是one-hot格式（即[0 0 0 1]这样的格式），
它的节点与隐层节点个数一致，
它的值由隐层节点竞争得到，即隐层节点哪个值最大，对应的输出节点就为1，其余为0。

  带隐层拓扑的网络拓扑图

往往还会把隐层节点之间的拓扑结构一起画上，
则SOM的网络拓扑图会如下：

PASS:输出节点之间的拓扑结构对于最终模型的应用上是没有任何影响的，它只是在训练过程中需要使用。

  04.  SOM的模型表达式

SOM的模型数学表达式为：

$\text{y} = \textbf{compet}(-\textbf{dist}(x,W))$

其中，

●  dist 为x和W的欧氏距离

例如，2输出3隐节点时， , $W = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \\ w_{31} & w_{32} \end{bmatrix}$

则：

$\displaystyle \textbf{dist}(x,W) = \begin{bmatrix} \sqrt{(x_1- w_{11})^2+(x_1- w_{12})^2} \\ \\ \sqrt{(x_1- w_{21})^2+(x_1- w_{22})^2}\\ \\ \sqrt{(x_1- w_{31})^2+(x_1- w_{32})^2} \end{bmatrix}$

●  compet 为竞争函数,

它将向量最大的值置为1，其实置0
例如，compet([ 2 5 3 ]) = [ 0 1 0 ]

SOM模型输出的计算，简单来说，就是x离W哪行最近，就为1，其余为0.

背后意义就是离哪个聚类中心点近，就判为哪个聚类点。

  编后语

本文我们先大概摸清SOM神经网络是什么，
它的思路其实并不复杂，只是Kohonen的基础上，在隐节点引入了一个拓扑结构来定义邻域
由于我们往往看到的基本都是带隐节点拓扑结构的网络拓扑图，很容易产生误会，以为隐层节点间相互连接，
其实隐节点的拓扑图只在训练阶段用于获取邻域节点，与最终的模型并没有任何关系。
在接下来的文章，我们把SOM的代码按matlab内部逻辑实现后，我们将更清晰SOM算法的具体细节与算法流程。

二、SOM-代码重写(单样本训练)

本文是笔者细扒matlab2009b神经网络工具箱newsom的源码，

在源码的基础上去除冗余代码，重现的简版newsom代码，代码与newsom的结果完全一致。
通过本代码的学习，可以完全细节的了解SOM单样本训练的实现逻辑。

  01. 代码结构说明

代码主要包含了三个函数：   testSomNet      trainSomNet      predictSomNet

testSomNet:  测试用例主函数，直接运行时就是执行该函数。

1、数据生成：随机生成一组训练数据，
2、用自写的函数训练一个SOM网络，与预测结果。
3、使用工具箱训练一个SOM网络。
4、比较自写函数与工具箱训练结果是否一致(权重、训练误差的比较)

trainSomNet：网络训练主函数，用于训练一个SOM神经网络。

单样本训练方式，训练一个SOM神经网络

predictSomNet：用训练好的网络进行预测。

传入需要预测的X，与网络的权重矩阵，即可得到预测结果。

02. 代码运行结果解说

运行代码后，得到预测结果与对比结果，如下：

从中可以看到，自写代码与工具箱的逻辑一致。

03. 具体代码

matlab2009b亲测已跑通：
```
%------------测试DEMO函数------------------
function testSomNet()
%本代码来自bp.bbbdata.com
%本代码模仿matlab神经网络工具箱的newsom神经网络，用于训练《SOM神经网络》,
%本代码扒自matlab2009b,使用的是旧版newsom单样本训练算法，在新版matlab中不再使用。
%代码主旨用于教学,供大家学习理解newsom神经网络原理
% ---------数据生成与参数预设-------------
% 数据生成
rand('seed',70);
X = [rand(1,400)*2; rand(1,400)];    % 生成样本
test_x = [0.5 0.6;0.5 0.6];                  % 测试样本
epochs = 10;                         % 训练步数
dimensions = [4 3];                  % 输出节点拓扑维度
 
%---------调用自写函数进行训练--------------
rand('seed',70);
w = trainSomNet(X,dimensions,epochs);
py = find(predictSomNet(w,test_x))
 
% -----调用工具箱，与工具箱的结果比较------
% 调用工具箱进行训练
rand('seed',70);
Xr = [min(X,[],2),max(X,[],2)];
net = newsom(Xr,dimensions);
net.trainParam.epochs = epochs;
net = train(net,X);
 
% 工具箱的结果
pyByTool = find(sim(net,test_x))
w_tools  = net.IW{1};
 
% 与工具箱的差异
maxECompareNet = max([max(abs(w(:)-w_tools(:))),max(abs(pyByTool(:)-py(:)))]);
disp(['自写代码与工具箱权重阈值的最大差异:',num2str(maxECompareNet)])
 
end
 
% -----------SOM的训练函数----------------------
function w = trainSomNet(X,dimensions,epochs)
[xn,sn] = size(X);                % 输入个数，样本个数
hn      = prod(dimensions);       % 隐节点个数
 
% ----生成隐节点拓扑结构并计算矩阵矩阵-----------
pos     = hextop(dimensions);     % 生成隐节点拓扑结构
d       = linkdist(pos);          % 隐节点拓扑结构距离矩阵
 
% --------参数设置--------------
order_steps = 1000;               % 收缩步数阈值
order_lr    = 0.9;                % 初始学习率
tune_lr     = 0.02;               % 学习率收缩阈值
nd_max      = max(max(d));        % 初始邻域距离
tune_nd     = 1 ;                 % 邻域距离收缩阈值
 
%-----初始化w：取每个输入的中心点-------------------
x_mid  = (min(X,[],2)+max(X,[],2))/2;         % 计算输入的中心点
w      = repmat(x_mid',hn,1);                 % 初始化w
 
% ---------训练-----------------------------
step   = 0;
for epoch=1:epochs
    for i=1:sn
        idx   = fix(rand*sn) + 1;         % 随机选择一个样本
        cur_x = X(:,idx);                 % 当前选择的样本
 
        if (step < order_steps)             % 小于order_steps时，线性收缩学习率与邻域
            percent = 1 - step/order_steps;
            nd      = 1.00001 + (nd_max-1) * percent;
            lr      = tune_lr + (order_lr-tune_lr) * percent;
        else                                % >=order_steps时，幂收缩学习率，邻域则不再变化
            nd      = tune_nd + 0.00001;
            lr      = tune_lr * order_steps/step;
        end
        
        a     = predictSomNet(w,cur_x);          % 网络的预测值
        lr_a = lr * 0.5*(a + (d < nd)*a);        % 计算邻域内的节点学习率
       
        % 计算dw
        dw   = zeros(hn,xn);                 
        dw   = dw +repmat(lr_a,1,xn) .* (repmat(cur_x',hn,1)-w);
        
        % 更新w
        w    = w + dw;  
        step = step + 1;
    end
end
 
end
 
% --------SOM的预测函数---------------
function y = predictSomNet(w,X)
 
% 计算隐节点激活值
z = zeros(size(w,1),size(X,2));
for i= 1: size(X,2)
    cur_x = X(:,i);
    z(:,i) = -sum((repmat(cur_x',size(w,1),1)-w).^ 2,2) .^ 0.5;
end
% 通过隐节点竞争得到输出
[~,idx] = max(z);% 找出最大值
y = z*0;
y(idx+ size(y,1)*(0:size(y,2)-1)) = 1;
 
end
 
```
注意：本代码是matlab旧版本神经网络工具箱som代码的逻辑,在新版本上与newsom结果会不一致。

相关文章

《BP神经网络梯度推导》

《BP神经网络提取的数学表达式》

《一个BP的完整建模流程》
相关阅读:
NoSQL
.NET CLR介绍
 DASCTF X GFCTF 2022十月挑战赛 - pwn
DSP2335的按键输入key工程笔记
 npm install 下载不下来依赖解决方案
 如何系统的自学python
编译后的go程序无法在alpine基础镜像创建的容器运行问题
 RedHat上部署kubernetes dashboard 2.7
Redis特性与应用场景
 PTL电子标签助力仓储行业转型升级提升拣货效率降低误差率
原文地址：https://blog.csdn.net/dbat2015/article/details/125469975

一、入门原理解说

01. 基于Kohonen规则的聚类算法

02. SOM聚类的思想

03. SOM神经网络的拓扑图

04. SOM的模型表达式

编后语

二、SOM-代码重写(单样本训练)

01. 代码结构说明

02. 代码运行结果解说

03. 具体代码