神经网络(neural networks)是仿照动物的神经系统而来，期望机器可以获得类似人类的学习的能力。

一、神经元模型

神经网络中最基本的模型叫做神经元（neuron）或者（unit）。1943年， McCulloch and Pitts 按照生物神经元的功能（兴奋的接受，传递）抽象出神经元模型，即"M-P神经元模型"。

上图中，表示来自n个其他神经元的输入信号，为这个n信号的权重。神经元收到这些输入之后，会计算总输入值,并将总输入值与当前神经元的阈值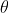进行比较，然后通过激活函数（activation function）处理以产生神经元的输出。

 激活函数的理想形态应该是如下图所示的阶跃函数，即将输出映射成“0”（表示神经元兴奋）或者“1”（表示神经元抑制）。

 但是阶跃函数不连续，不光滑，在实际数据计算中不太友好。所以常用Sigmoid函数作为激活函数。

整个神经元模型可以表示为：

 

二、感知机与多层网络

感知机（perceptron）由两层神经元组成，输入层接收外界输入信号后传递给输出层，输出层是M-P神经元，亦称“阈值逻辑单元”(threshold logic unit)。

感知机能够方便的实现与或非逻辑运算。 假定 激活函数为阶跃函数，即

• 与运算： 
  • 什么是与运算：
    • 输入取值范围{1,0}
    •  运算：
  • 设定，感知机可以表示为。验证与运算的情况：
    • 输入为[1, 1], 
    • 输入为[0,1], 
    • 输入为[1,0],
    • 输入为[0,0], 
  • 只有输入为[1,1]的时候，感知机的输出为1。其余输入条件下，感知机输出为0
• 或运算
  • 什么是或运算
    • 输入取值范围是{1,0}
    • 运算：
  • 设定感知机可以表示为，验证或运算的情况：
    • 输入为[1, 1], 
    • 输入为[0,1], 
    • 输入为[1,0], 
    • 输入为[0,0],  
  • 输入有一个为1时，输出为1。否则感知机输出为0.
• 非运算
  • 输入取值范围{1,0}
  • 运算：
  • 设,感知机可以表示为，验证非运算情况：
    • 输入为1，输出为
    • 输入为0，输出为
• 感知机的权重学习过程（可以看做是的权重）:

其中,叫做学习率。

感知机是单层神经元，适合处理线性可分问题。如果线性不可分感知机学习的过程会发生震荡，难以求得合适解，需要引入多层神经网络。

 神经网络需要学习的是连接权和阈值。

三、误差逆转传播算法

误差逆传播（error backPropagation, 简称BP）算法可以用于多种神经网络模型的学习。

四、全局最小和局部极小

五、其他常见神经网络

六、深度学习